小学数学人教版五年级下册3 长方体与正方体提高版(pdf版学案)
文档属性
| 名称 | 小学数学人教版五年级下册3 长方体与正方体提高版(pdf版学案) |  | |
| 格式 | zip | ||
| 文件大小 | 209.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 20:50:31 | ||
图片预览




文档简介
1
长方体与正方体提高训练
学习目标:
1.理解表面积的意义,掌握表面积的计算方法;
2.体积和容积的意义及度量单位,会进行单位间的换算;
3.感受有关体积和容积单位的实际意义;
4.结合具体情境,探索并掌握长方体和正方体的体积和表面积的计算方法;
知识整理
【知识点 1】长方体与正方体的认识
【知识点 2】长方体与正方体的棱长和
1.长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4
2.正方体棱长和=棱长×12 棱长=棱长和÷12
【知识点 3】长方体与正方体的表面积
1.长方体表面积=(长×宽+长×高+宽×高)×2 =(a×b+a×c+b×c)×2
=(前面面积+上面面积+右面面积)×2
2.正方体表面积=棱长×棱长×6=a×a×6=6a? =任意一个面的面积×6
【知识点 3】长方体与正方体的体积
1.长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
2.长方体和正方体的体积=底面积×高=右面面积×长=前面面积×宽
例题讲解
2
例 1:一个长方体的礼堂如图,过节时需要在四周装上成串的彩灯,每串彩灯长 2m,一共需
要多少串彩灯?
【变式练习】
1.(1)一个长方体棱长和 164cm,已知长方体的底面周长为 72cm,长方体的高是多少 cm?
(2)一个长方体棱长和 164cm,已知长方体的左面周长为 40cm,长方体的长是多少 cm?
(3)一个长方体棱长和 164cm,已知长方体的正面周长为 56cm,长方体的宽是多少 cm?
2.一个长方体长 12 厘米宽 8厘米高 7 厘米,把它切成一个尽可能大的正方体,这个正方体
的棱长是多少厘米?
3.一种礼品盒,长 30 厘米,宽 25 厘米,高 20 厘米。如果要用红丝线按下图所示方法把它
捆扎起来,结头处丝线留出 30 厘米,至少需要多少米丝线?
例 2:一个房间的长 6 米,宽 3.5 米,高 3 米,门窗面积是 8 平方米。现在要把这个房间的四
壁和顶面粉刷水泥,粉刷水泥的面积是多少平方米?如果每平方米需要水泥 4 千克,一共要
水泥多少千克?
【变式练习】
3
1.一只鱼缸,棱长和为 280cm,其中,底面周长为 50cm,右面周长为 40cm,前面周长为 50cm,
这只鱼缸的占地面积是多少平方厘米?
2.一块长方形铁片(厚度不计),四个角剪去边长为 2.8 分米的正方形,焊成一个长方体铁
皮盒,可以盛水 546 升。已知这块长方形铁皮的长是 21.2 分米,求长方形铁皮的面积。
3.一块长方形铁皮长 60 厘米,宽 40 厘米,如 图, 从四个角上剪去边长是 10 厘米的正方
形,然后做成盒子,这个盒子的表面积是多少平方厘米?
例 3:把一个长、宽、高分别是 7 厘米、6 厘米、5 厘米的长方体截成两个长方体,使这两个
长方体的表面积的和最大,这时表面积之和是多少平方厘米?
【变式练习】
1.一个长 5 厘米,宽 4厘米,高 3厘米的长方体,截成两个形状,大小完全一样的长方体,
表面积最多能增加多少平方厘米?
4
2.一根 1.8m 长的木材,锯成三个完全相同的正方体后,表面积比原来增加多少平方厘米?
3.把一个长 18 厘米,宽 12 厘米,高 6厘米的长方体木块截成两个表面积相等的长方体,表
面积最小的长方体的表面积是多少?表面积最大的长方体的表面积是多少?
例 4:一位美术老师在课堂上进行立体模型素描教学时,把 14 个棱长为 1分米的正方体摆在
课桌上成如图形状,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为
( )。
【变式练习】
1.小明自己动手烤了一块正方体大蛋糕,蛋糕的表面呈咖啡色,里面是淡黄色。小明想慢慢
享用自己的劳动成果,于是他将这块蛋糕切成了如图所示的 125(5×5×5)块同样大小的
小正方体蛋糕。切完后他发现,有的小蛋糕有咖啡色的面,而有的没有咖啡色的面,那么
一块小正方体蛋糕最多 有( )个面是咖啡色,没有咖啡色的面和只有两面是咖啡色
的小正方体蛋糕的总数分别是( )块和( )块。
2.如图是一个表面涂满了红色的正方体,在它的每个面上都等距离地切两刀。问:
(1)三个面涂有红色的有几个?(2)两个面涂有红色的有几个?
(3)一个面涂有红色的有几个?(4)都没有红色的有几个?
5
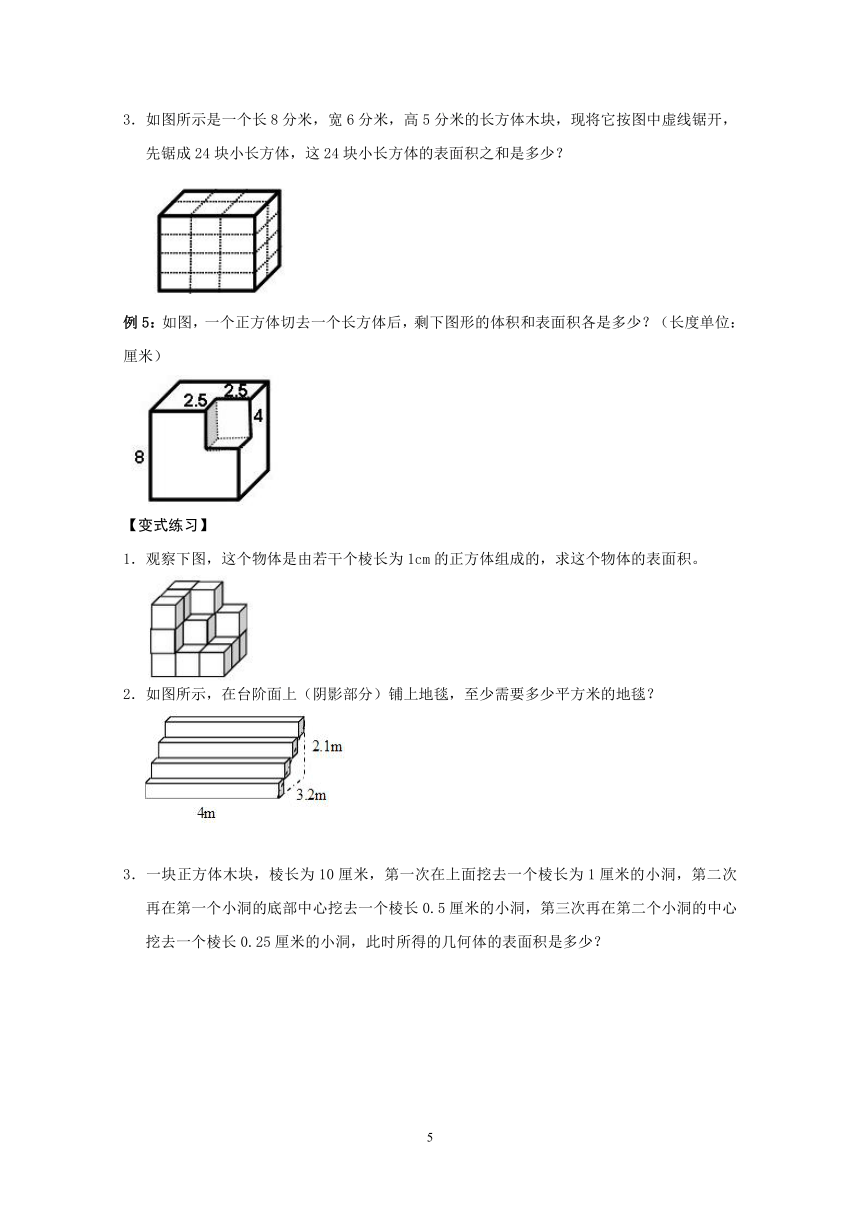
3.如图所示是一个长 8分米,宽 6分米,高 5 分米的长方体木块,现将它按图中虚线锯开,
先锯成 24 块小长方体,这 24 块小长方体的表面积之和是多少?
例 5:如图,一个正方体切去一个长方体后,剩下图形的体积和表面积各是多少?(长度单位:
厘米)
【变式练习】
1.观察下图,这个物体是由若干个棱长为 1cm 的正方体组成的,求这个物体的表面积。
2.如图所示,在台阶面上(阴影部分)铺上地毯,至少需要多少平方米的地毯?
3.一块正方体木块,棱长为 10 厘米,第一次在上面挖去一个棱长为 1 厘米的小洞,第二次
再在第一个小洞的底部中心挖去一个棱长 0.5 厘米的小洞,第三次再在第二个小洞的中心
挖去一个棱长 0.25 厘米的小洞,此时所得的几何体的表面积是多少?
6
例 6:有一块面积为 36 平方分米的铁皮,将其制作成可以容纳最多物体的形状,其棱长是多
少?可以容纳多少立方分米的物体?
【变式练习】
1.一个长方形的底面是一个周长为 16 分米的正方形,它的表面积是 96 平方分米,这个长方
体的体积是多少?
2.一个长方体,其中三个面的面积分别是 15 平方厘米,20 平方厘米,12 平方厘米,这个长
方体的体积是多少立方厘米?
3.一个长方体和一个正方体的棱长之和相等。已知长方体的长是 6 分米,宽是 4 分米,高是
2分米,求正方体的表面积和体积?
例 7:一个长方体玻璃容器,从里面量长 2 分米,宽 1.5 分米,高 1.8 分米,里面盛了一半水,
现在将体积为 0.6 立方分米的玻璃球全部浸入水中,这时水面高度多少分米?
【变式练习】
7
1.在一个长 60 厘米,宽 54 厘米,深 45 厘米的长方体鱼缸里放入一些水,并在水中浸入一
块长 12 厘米,宽 18 厘米,高 15 厘米的铁块,把铁块从水中取出,水面将下降多少厘米?
2.一个长方体容器,底面是一个边长为 60 厘米的正方形,容器里直立着一个高 1 米,底面
边长为 15 厘米的长方体铁块,这时容器里的水深为 0.5 米。现在把铁块轻轻地向上提起
24 厘米,那么露出水面的铁块上被水浸湿的部分长多少厘米?
3.一个长方体水箱,长 30 厘米,宽 42 厘米,水箱里装着水,并有一个长 21 厘米,宽 15 厘
米的小长方体铁块完全浸没在水中,当把水中的铁块取出后,水面下降了 1 厘米,铁块的
高是多少厘米?
例 8:一个长方体,如果从它的高度方向锯掉 3 厘米的一段,正好得到一个正方体,但表面积
减少了 72 平方厘米,原来长方体的体积是多少?
【变式练习】
1.一个长方体,如果长增加 5 厘米,则体积增加 150 立方厘米;如果宽增加 4 厘米,则体积
增加 160 立方厘米;如果高增加 3 厘米,则体积增加 144 立方厘米。问原长方体的表面积
是多少平方厘米?
8
2.一个长 40 厘米的长方体,它的横截面是正方形,如果长增加 5厘米,表面积就增加 80 平
方厘米,原长方体的体积是多少?
3.一个长方体木块,从下部和上部分别截去高为 3 厘米和 2 厘米的长方体后,便成为一个正
方体,其表面积减少了 120 平方厘米。原来长方体的体积是多少立方厘米?
课后巩固
1.有一个长方体形状的零件,中间挖去一个正方体的孔(如图),你能算出它的体积和表面
积吗?(单位:厘米)
2.有一个形状如下图的零件,求它的体积和表面积。(单位:厘米)
9
1.一根长 80 厘米,宽和高都是 12 厘米的长方体钢材,从钢材的一端锯下一个最大的正方体
后,它的表面积减少了多少平方厘米?
2.把 4 块棱长都是 2 分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方分米?
3.有两个长方体水缸,甲缸长 3 分米,宽和高都是 2 分米;乙缸长 4 分米、宽 2 分米,里面
的水深 1.5 分米。现把乙缸中的水倒进甲缸,水在甲缸里深几分米?
4.有一块边长 2 分米的正方体铁块,现把它煅造成一根长方体,这长方体的截面是一个长 4
厘米、宽 2厘米的长方形,求它的长。
5.有一块边长是 5厘米的正方体铁块,浸没在一个长方体容器里的水中。取出铁后,水面下
降了 0.5 厘米。这个长方体容器的底面积是多少平方厘米?
6.有两个无盖的长方体水箱,甲水箱里有水,乙水箱空着。从里面量,甲水箱长 40 厘米,
宽 32 厘米,水面高 20 厘米;乙水箱长 30 厘米,宽 24 厘米,深 25 厘米。将甲水箱中部
分水倒入乙水箱,使两箱水面高度一样,现在水面高多少厘米?
10
7.把一个棱长是 5厘米的正方体的六个面涂满红色,然后切成 1 立方厘米的小正方体,这些
小正方体中,一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有
多少个?
8.把若干个体积相同的小正方体堆成一个大的正方体,然后在大正方体的表面涂上颜色,已
知两面被涂上红色的小正方体共有 24 个,那么,这些小正方体一共有多少个?
9.有一个正方体木块,长 4 分米、宽 3 分米、高 6 分米,现在把它锯成两个长方体,表面积
最多增加多少平方分米?
10.有三块完全一样的长方体积木,它们的长是 8 厘米、宽 4 厘米、高 2 厘米,现把三块积
木拱成一个大的长方体,怎样搭表面积最大?最大是多少平方厘米?
11.一个长方体,不同的三个面的面积分别是 35 平方厘米、21 平方厘米和 15 平方厘米,且
长、宽、高都是质数,这个长方体的体积是多少立方厘米?
11
12.一个长方体的体积是 48 立方厘米,并且长、宽、高是三个连续的偶数。这个长方体的表
面积是多少平方厘米?
13.有一个长方体,它的底面是一个正方形,它的表面积是 190 平方厘米,如果用一个平行
于底面的平面将它截成两个长方体,则两个长方体表面积的和为 240 平方厘米,求原来
长方体的体积。
14.18 个边长为 2厘米的小正方体堆成如图的形状,求它的表面积。
15.有大、中、小三个正方体水池,它们的内边长分别为 4米、3 米、2 米。把两堆碎石分别
沉没在中、小水池的水中,两个水池的水面分别升高了 4 厘米和 11 厘米,如果将这两堆
碎石都沉没在大水池中,那么大水池水面将升高多少厘米?
长方体与正方体提高训练
学习目标:
1.理解表面积的意义,掌握表面积的计算方法;
2.体积和容积的意义及度量单位,会进行单位间的换算;
3.感受有关体积和容积单位的实际意义;
4.结合具体情境,探索并掌握长方体和正方体的体积和表面积的计算方法;
知识整理
【知识点 1】长方体与正方体的认识
【知识点 2】长方体与正方体的棱长和
1.长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4
2.正方体棱长和=棱长×12 棱长=棱长和÷12
【知识点 3】长方体与正方体的表面积
1.长方体表面积=(长×宽+长×高+宽×高)×2 =(a×b+a×c+b×c)×2
=(前面面积+上面面积+右面面积)×2
2.正方体表面积=棱长×棱长×6=a×a×6=6a? =任意一个面的面积×6
【知识点 3】长方体与正方体的体积
1.长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
2.长方体和正方体的体积=底面积×高=右面面积×长=前面面积×宽
例题讲解
2
例 1:一个长方体的礼堂如图,过节时需要在四周装上成串的彩灯,每串彩灯长 2m,一共需
要多少串彩灯?
【变式练习】
1.(1)一个长方体棱长和 164cm,已知长方体的底面周长为 72cm,长方体的高是多少 cm?
(2)一个长方体棱长和 164cm,已知长方体的左面周长为 40cm,长方体的长是多少 cm?
(3)一个长方体棱长和 164cm,已知长方体的正面周长为 56cm,长方体的宽是多少 cm?
2.一个长方体长 12 厘米宽 8厘米高 7 厘米,把它切成一个尽可能大的正方体,这个正方体
的棱长是多少厘米?
3.一种礼品盒,长 30 厘米,宽 25 厘米,高 20 厘米。如果要用红丝线按下图所示方法把它
捆扎起来,结头处丝线留出 30 厘米,至少需要多少米丝线?
例 2:一个房间的长 6 米,宽 3.5 米,高 3 米,门窗面积是 8 平方米。现在要把这个房间的四
壁和顶面粉刷水泥,粉刷水泥的面积是多少平方米?如果每平方米需要水泥 4 千克,一共要
水泥多少千克?
【变式练习】
3
1.一只鱼缸,棱长和为 280cm,其中,底面周长为 50cm,右面周长为 40cm,前面周长为 50cm,
这只鱼缸的占地面积是多少平方厘米?
2.一块长方形铁片(厚度不计),四个角剪去边长为 2.8 分米的正方形,焊成一个长方体铁
皮盒,可以盛水 546 升。已知这块长方形铁皮的长是 21.2 分米,求长方形铁皮的面积。
3.一块长方形铁皮长 60 厘米,宽 40 厘米,如 图, 从四个角上剪去边长是 10 厘米的正方
形,然后做成盒子,这个盒子的表面积是多少平方厘米?
例 3:把一个长、宽、高分别是 7 厘米、6 厘米、5 厘米的长方体截成两个长方体,使这两个
长方体的表面积的和最大,这时表面积之和是多少平方厘米?
【变式练习】
1.一个长 5 厘米,宽 4厘米,高 3厘米的长方体,截成两个形状,大小完全一样的长方体,
表面积最多能增加多少平方厘米?
4
2.一根 1.8m 长的木材,锯成三个完全相同的正方体后,表面积比原来增加多少平方厘米?
3.把一个长 18 厘米,宽 12 厘米,高 6厘米的长方体木块截成两个表面积相等的长方体,表
面积最小的长方体的表面积是多少?表面积最大的长方体的表面积是多少?
例 4:一位美术老师在课堂上进行立体模型素描教学时,把 14 个棱长为 1分米的正方体摆在
课桌上成如图形状,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为
( )。
【变式练习】
1.小明自己动手烤了一块正方体大蛋糕,蛋糕的表面呈咖啡色,里面是淡黄色。小明想慢慢
享用自己的劳动成果,于是他将这块蛋糕切成了如图所示的 125(5×5×5)块同样大小的
小正方体蛋糕。切完后他发现,有的小蛋糕有咖啡色的面,而有的没有咖啡色的面,那么
一块小正方体蛋糕最多 有( )个面是咖啡色,没有咖啡色的面和只有两面是咖啡色
的小正方体蛋糕的总数分别是( )块和( )块。
2.如图是一个表面涂满了红色的正方体,在它的每个面上都等距离地切两刀。问:
(1)三个面涂有红色的有几个?(2)两个面涂有红色的有几个?
(3)一个面涂有红色的有几个?(4)都没有红色的有几个?
5
3.如图所示是一个长 8分米,宽 6分米,高 5 分米的长方体木块,现将它按图中虚线锯开,
先锯成 24 块小长方体,这 24 块小长方体的表面积之和是多少?
例 5:如图,一个正方体切去一个长方体后,剩下图形的体积和表面积各是多少?(长度单位:
厘米)
【变式练习】
1.观察下图,这个物体是由若干个棱长为 1cm 的正方体组成的,求这个物体的表面积。
2.如图所示,在台阶面上(阴影部分)铺上地毯,至少需要多少平方米的地毯?
3.一块正方体木块,棱长为 10 厘米,第一次在上面挖去一个棱长为 1 厘米的小洞,第二次
再在第一个小洞的底部中心挖去一个棱长 0.5 厘米的小洞,第三次再在第二个小洞的中心
挖去一个棱长 0.25 厘米的小洞,此时所得的几何体的表面积是多少?
6
例 6:有一块面积为 36 平方分米的铁皮,将其制作成可以容纳最多物体的形状,其棱长是多
少?可以容纳多少立方分米的物体?
【变式练习】
1.一个长方形的底面是一个周长为 16 分米的正方形,它的表面积是 96 平方分米,这个长方
体的体积是多少?
2.一个长方体,其中三个面的面积分别是 15 平方厘米,20 平方厘米,12 平方厘米,这个长
方体的体积是多少立方厘米?
3.一个长方体和一个正方体的棱长之和相等。已知长方体的长是 6 分米,宽是 4 分米,高是
2分米,求正方体的表面积和体积?
例 7:一个长方体玻璃容器,从里面量长 2 分米,宽 1.5 分米,高 1.8 分米,里面盛了一半水,
现在将体积为 0.6 立方分米的玻璃球全部浸入水中,这时水面高度多少分米?
【变式练习】
7
1.在一个长 60 厘米,宽 54 厘米,深 45 厘米的长方体鱼缸里放入一些水,并在水中浸入一
块长 12 厘米,宽 18 厘米,高 15 厘米的铁块,把铁块从水中取出,水面将下降多少厘米?
2.一个长方体容器,底面是一个边长为 60 厘米的正方形,容器里直立着一个高 1 米,底面
边长为 15 厘米的长方体铁块,这时容器里的水深为 0.5 米。现在把铁块轻轻地向上提起
24 厘米,那么露出水面的铁块上被水浸湿的部分长多少厘米?
3.一个长方体水箱,长 30 厘米,宽 42 厘米,水箱里装着水,并有一个长 21 厘米,宽 15 厘
米的小长方体铁块完全浸没在水中,当把水中的铁块取出后,水面下降了 1 厘米,铁块的
高是多少厘米?
例 8:一个长方体,如果从它的高度方向锯掉 3 厘米的一段,正好得到一个正方体,但表面积
减少了 72 平方厘米,原来长方体的体积是多少?
【变式练习】
1.一个长方体,如果长增加 5 厘米,则体积增加 150 立方厘米;如果宽增加 4 厘米,则体积
增加 160 立方厘米;如果高增加 3 厘米,则体积增加 144 立方厘米。问原长方体的表面积
是多少平方厘米?
8
2.一个长 40 厘米的长方体,它的横截面是正方形,如果长增加 5厘米,表面积就增加 80 平
方厘米,原长方体的体积是多少?
3.一个长方体木块,从下部和上部分别截去高为 3 厘米和 2 厘米的长方体后,便成为一个正
方体,其表面积减少了 120 平方厘米。原来长方体的体积是多少立方厘米?
课后巩固
1.有一个长方体形状的零件,中间挖去一个正方体的孔(如图),你能算出它的体积和表面
积吗?(单位:厘米)
2.有一个形状如下图的零件,求它的体积和表面积。(单位:厘米)
9
1.一根长 80 厘米,宽和高都是 12 厘米的长方体钢材,从钢材的一端锯下一个最大的正方体
后,它的表面积减少了多少平方厘米?
2.把 4 块棱长都是 2 分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方分米?
3.有两个长方体水缸,甲缸长 3 分米,宽和高都是 2 分米;乙缸长 4 分米、宽 2 分米,里面
的水深 1.5 分米。现把乙缸中的水倒进甲缸,水在甲缸里深几分米?
4.有一块边长 2 分米的正方体铁块,现把它煅造成一根长方体,这长方体的截面是一个长 4
厘米、宽 2厘米的长方形,求它的长。
5.有一块边长是 5厘米的正方体铁块,浸没在一个长方体容器里的水中。取出铁后,水面下
降了 0.5 厘米。这个长方体容器的底面积是多少平方厘米?
6.有两个无盖的长方体水箱,甲水箱里有水,乙水箱空着。从里面量,甲水箱长 40 厘米,
宽 32 厘米,水面高 20 厘米;乙水箱长 30 厘米,宽 24 厘米,深 25 厘米。将甲水箱中部
分水倒入乙水箱,使两箱水面高度一样,现在水面高多少厘米?
10
7.把一个棱长是 5厘米的正方体的六个面涂满红色,然后切成 1 立方厘米的小正方体,这些
小正方体中,一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有
多少个?
8.把若干个体积相同的小正方体堆成一个大的正方体,然后在大正方体的表面涂上颜色,已
知两面被涂上红色的小正方体共有 24 个,那么,这些小正方体一共有多少个?
9.有一个正方体木块,长 4 分米、宽 3 分米、高 6 分米,现在把它锯成两个长方体,表面积
最多增加多少平方分米?
10.有三块完全一样的长方体积木,它们的长是 8 厘米、宽 4 厘米、高 2 厘米,现把三块积
木拱成一个大的长方体,怎样搭表面积最大?最大是多少平方厘米?
11.一个长方体,不同的三个面的面积分别是 35 平方厘米、21 平方厘米和 15 平方厘米,且
长、宽、高都是质数,这个长方体的体积是多少立方厘米?
11
12.一个长方体的体积是 48 立方厘米,并且长、宽、高是三个连续的偶数。这个长方体的表
面积是多少平方厘米?
13.有一个长方体,它的底面是一个正方形,它的表面积是 190 平方厘米,如果用一个平行
于底面的平面将它截成两个长方体,则两个长方体表面积的和为 240 平方厘米,求原来
长方体的体积。
14.18 个边长为 2厘米的小正方体堆成如图的形状,求它的表面积。
15.有大、中、小三个正方体水池,它们的内边长分别为 4米、3 米、2 米。把两堆碎石分别
沉没在中、小水池的水中,两个水池的水面分别升高了 4 厘米和 11 厘米,如果将这两堆
碎石都沉没在大水池中,那么大水池水面将升高多少厘米?
