冀教版数学四年级下册:第3单元 三位数乘两位数-教学课件 58张PPT
文档属性
| 名称 | 冀教版数学四年级下册:第3单元 三位数乘两位数-教学课件 58张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 00:00:00 | ||
图片预览








文档简介
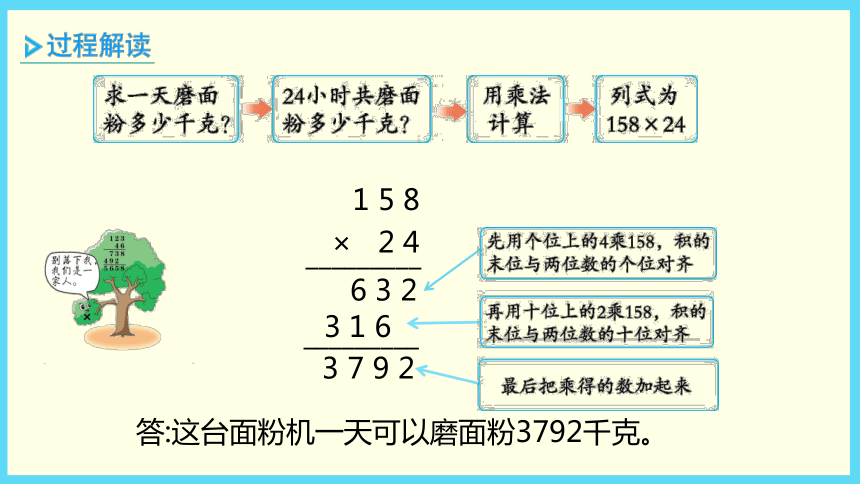
课件58张PPT。1 乘法第1课时 三位数乘两位数(教材P12)四年级数学·下 新课标[冀教] 第3单元 陈景润是一位家喻户晓的数学家,在攻克哥德巴赫猜想方面作出了重大贡献,创立了著名的“陈氏定理”,所以有许多人亲切地称他为“数学王子”。 一台面粉机每小时磨面粉158千克,这台面粉机一天可以磨面粉多少千克?1 5 8× 2 4__________________6 3 23 7 9 23 1 6答:这台面粉机一天可以磨面粉3792千克。巧学妙记三位数乘两位数,计算法则要记住 。个位先乘是规律,个位对齐记仔细 。十位再乘要记住,积的末位十位齐 。两次的积来相加,计算准确是第一 。三位数乘两位数的笔算方法:
① 用两位数个位上的数去乘三位数,得数的末位和两位数的个位对齐;
② 用两位数十位上的数去乘三位数,得数的末位和两位数的十位对齐;
③ 把两次乘得的积加起来。1 乘法第2课时 因数末尾有0的三位数乘两位数
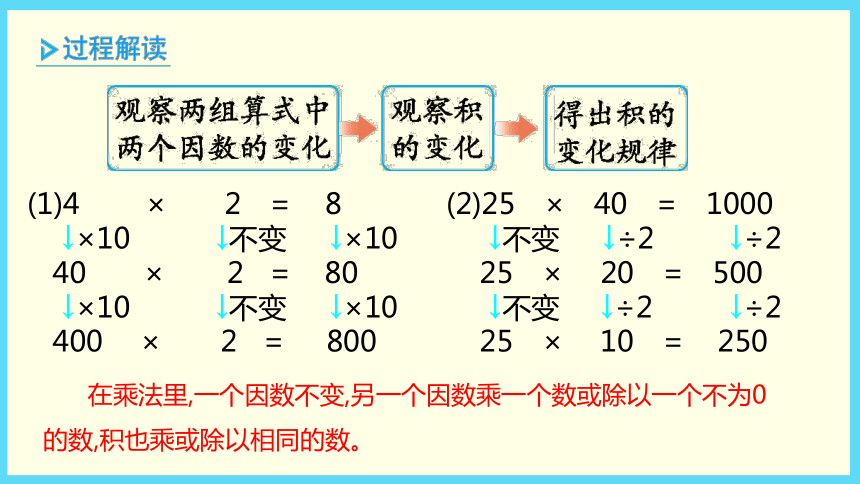
的乘法(教材P14)四年级数学·下 新课标[冀教] 第3单元龟兔赛跑观察下面两组题,你发现了什么?(1) 4×2=8
40×2=80
400×2=800 (2) 25×40=1000
25×20=500
25×10=250 探索积的变化规律的过程蕴含着归纳思想。 (2)25 × 40 = 1000
↓不变 ↓÷2 ↓÷2
25 × 20 = 500
↓不变 ↓÷2 ↓÷2
25 × 10 = 250(1)4 × 2 = 8
↓×10 ↓不变 ↓×10
40 × 2 = 80
↓×10 ↓不变 ↓×10
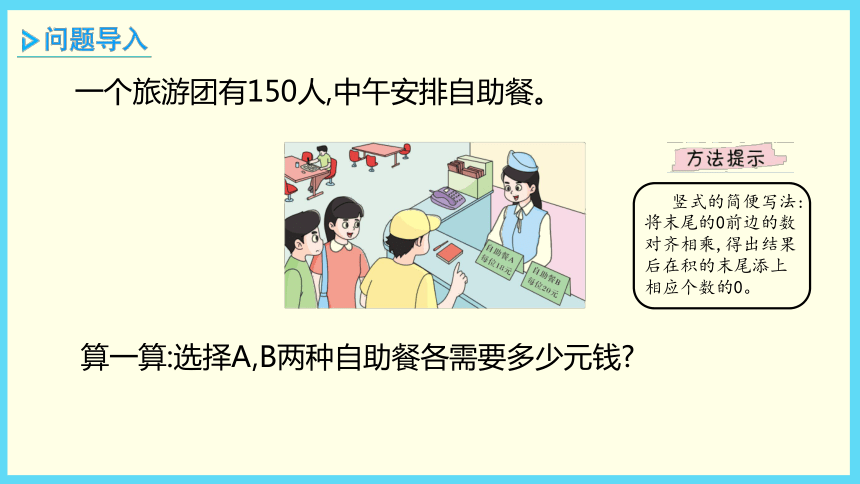
400 × 2 = 800 在乘法里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。 积的变化规律:在乘法里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。一个旅游团有150人,中午安排自助餐。算一算:选择A,B两种自助餐各需要多少元钱? 竖式的简便写法:将末尾的0前边的数对齐相乘,得出结果后在积的末尾添上相应个数的0。(1) 选择A种自助餐。150×18=2700(元)1 5 0× 1 8________1 2 0 01 5________2 7 0 0(2) 选择B种自助餐。150×20=3000(元)1 5 0× 2 03 0 0 0________一个旅游团有150人,中午安排自助餐。算一算:选择A,B两种自助餐各需要多少元钱?选自助餐A: 150×18=2700(元)选自助餐B: 150×20=3000(元)答:选择自助餐A需要2700元,选择自助餐B需要3000元。巧学妙记末尾有0数相乘,将0前数先对齐。再把0前数相乘,积的末尾再添0。 因数末尾有0的乘法的简便算法:先把0前面的数相乘,再看两个因数末尾一共有几个0,就在积的末尾添几个0。1 乘法第3课时 乘法的估算(教材P16)四年级数学·下 新课标[冀教] 第3单元估计一下:一个西瓜和一个哈密瓜,哪个重?(1)估算一下:这列火车大约有多少个座位?(2)算一算:这列火车实际有多少个座位?把因数看作与它接近的整十数或整百数进行估算。 方法一 118×12≈1200(个)
120×10=1200(个) 方法二 118×12≈1180(个)
118×10=1180(个)(1)118×12≈120×10=1200(个)(2)118×12=1416(个)巧学妙记乘法估算不用慌,四舍五入来帮忙。乘法估算并不难,凑十凑百来计算。1.估算时所得的结果是近似数,所以用“≈”。2.估算时把因数看成与它接近的整十数或整百数,计算比较简便。3.估算时把一个因数估大一些,另一个因数估小一些,它们的积更接近准确值。2 数量关系 (教材P18~21)四年级数学·下 新课标[冀教] 第3单元下面的购物小票中,你能看到哪些购物信息呢?读下面的发票,从中你了解到哪些信息?发票中的单价、数量、金额各表示什么? 理清单价、数量、金额的关系是解决此题的关键。 育才小学买了62套课桌椅,每套108元,一共花了6696元,还买了14个书柜,每个215元,一共花了3010元。
发票中的单价指的是每件的价钱,数量是买的件数,金额是一共花了多少钱,这三者的关系是:单价×数量=总价。总价÷数量=单价 总价÷单价=数量单价×数量=总价
总价÷数量=单价
总价÷单价=数量 单价、数量和总价三者的数量关系:
单价×数量=总价
总价÷数量=单价
总价÷单价=数量观察下面的铁路示意图。解答下面的问题:
(1)一列快速客车从北京发车,平均每小时行118千米,5小时行多少千米?
118×5= (千米)
(2)一列普通客车从北京出发,平均每小时行98千米,7小时行多少千米?
98×7= (千米) 火车每小时行的千米数称为速度,一共行驶的千米数,称为路程。 在速度、时间、路程三个量中,知道其中任意两个量,就可以求出第三个量。(1)(2)(1)118×5=590(千米) 答:5小时行590千米。(2)98×7=686(千米)答:7小时行686千米。 速度有一种特殊的表示方式,比如:快速列车平均每小时行118千米,记作118千米/时,读作118千米每时。速度、时间和路程三者之间的数量关系:
速度×时间=路程
路程÷时间=速度
路程÷速度=时间3 乘法运算律第1课时 乘法交换律和乘法结合律(教材P22~23)四年级数学·下 新课标[冀教] 第3单元以物换物,等价交换用计算器计算,并在圈里填上合适的符号。645×3232×64546×20353×180180×53203×46===乘法交换律与前边学过的加法交换律类似,不要混淆哦!= 乘法交换律:两个因数相乘,交换因数的位置,积不变。如果用a表示一个因数,b表示另一个因数,乘法交换律可以写成:a×b=b×a。一共有多少箱饮料?方法一×(6×5) × 4 = 120(箱)方法二 4 × (6×5) = 120(箱)规范解答(6×5)×4方法一方法二= 30×4= 120(箱)6×(5×4)= 6×20= 120(箱)答:一共有120箱饮料。答:一共有120箱饮料。巧学妙记乘法运算能简便,结合交换常做伴。连乘算式才适用,复杂计算变简单。 乘法结合律:三个数相乘,先乘前两个数或先乘后两个数,积不变。如果用a,b,c分别表示三个数,乘法结合律可以写成:(a×b)×c=a×(b×c)。3 乘法运算律第2课时 乘法分配律及简单应用(教材P24)四年级数学·下 新课标[冀教] 第3单元 植树节前,四(4)班的同学们去公园植树。1组20人,2组和3组都是10人。现在有60棵苗,怎么分配合理呢?两扇屏风一共有多少块玻璃?方法一(1)根据“排数×每排的块数”求出每一扇屏风上的玻璃数。(2)把两扇屏风上的玻璃数加起来就是一共的玻璃数。
12×5+9×5方法二(1)先求出两扇屏风每排的玻璃数。(2)再根据“每排的数量×排数”求出一共的玻璃数。(12+9)×5两种计算方法不同,但结果相等,即12×5+9×5=(12+9)×5。 乘法分配律是乘加或乘减两种运算之间的一种规律,而乘法交换律和乘法结合律只是乘法运算的一种规律方法一12×5+9×5=60+45=105(块)(12+9)×5=21×5=105(块)方法二答:两扇屏风一共有105块玻璃。巧学妙记乘法分配律好记,正能用来也能逆。乘加乘减才适用,计算简便是目的。1.两个数的和乘一个数,等于这两个数分别乘这个数,再把它们的积相加,这就叫做乘法分配律。
2.如果用a,b,c分别表示三个数,那么乘法分配律可以写成:(a+b)×c=a×c+b×c,也可以写成(a+b)c=ac+bc。3 乘法运算律第3课时 乘法的简便运算(教材P26~27)四年级数学·下 新课标[冀教] 第3单元 德国大数学家高斯在上小学时,有一天数学老师要求全班同学计算1+2+3+4+…
+99+100。高斯一会就算出答案是5050,而其他同学算到头昏脑涨也算不出来,最后只有高斯的答案正确无误。高斯的算法是:1+100=101,2+99=101,…,50+51=101,他是让前后两项两两相加,就组成了50对和都是101的配对,即101×50=5050。善于思考的高斯就是这样很快算出答案的。学校组织高年级102名师生去春游。(1)算一算:师生这次春游共需要多少元钱?
(2)102人中有4位老师,有98名学生。这些学生应交多少元钱?
(3)去春游的学生中,有36名是五年级的学生,五年级学生应交多少元钱?交钱人数×平均每人的费用=这些人一共交的钱数。(1) 102×25= (元)
100+2(2) 98×25= (元)
100-2(3) 25×36= (元)
4×9(1) 102×25= (100+2)×25= 100×25+2×25= 2500+50= 2550(元)答:师生这次春游共需要
2550元钱。(2) 98×25= (100-2)×25= 100×25-2×25= 2500-50= 2450(元)答:这些学生应交2450元钱。(3) 25×36= 25×(4×9)= 25×4×9= 100×9= 900(元)答:五年级学生应交900元钱。 两个数相乘,有时可以根据因数的特点,先将其中一个因数写成两个数相加(或相减)的形式,再将相加(或相减)的两个数分别与另一个因数相乘,最后把两个积相加(或相减)。 两个因数相乘时,可以把其中的一个因数看作两个数相加、相减或相乘的形式,然后直接用乘法运算定律进行计算,这样可以使计算变得简便。再 见
① 用两位数个位上的数去乘三位数,得数的末位和两位数的个位对齐;
② 用两位数十位上的数去乘三位数,得数的末位和两位数的十位对齐;
③ 把两次乘得的积加起来。1 乘法第2课时 因数末尾有0的三位数乘两位数
的乘法(教材P14)四年级数学·下 新课标[冀教] 第3单元龟兔赛跑观察下面两组题,你发现了什么?(1) 4×2=8
40×2=80
400×2=800 (2) 25×40=1000
25×20=500
25×10=250 探索积的变化规律的过程蕴含着归纳思想。 (2)25 × 40 = 1000
↓不变 ↓÷2 ↓÷2
25 × 20 = 500
↓不变 ↓÷2 ↓÷2
25 × 10 = 250(1)4 × 2 = 8
↓×10 ↓不变 ↓×10
40 × 2 = 80
↓×10 ↓不变 ↓×10
400 × 2 = 800 在乘法里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。 积的变化规律:在乘法里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。一个旅游团有150人,中午安排自助餐。算一算:选择A,B两种自助餐各需要多少元钱? 竖式的简便写法:将末尾的0前边的数对齐相乘,得出结果后在积的末尾添上相应个数的0。(1) 选择A种自助餐。150×18=2700(元)1 5 0× 1 8________1 2 0 01 5________2 7 0 0(2) 选择B种自助餐。150×20=3000(元)1 5 0× 2 03 0 0 0________一个旅游团有150人,中午安排自助餐。算一算:选择A,B两种自助餐各需要多少元钱?选自助餐A: 150×18=2700(元)选自助餐B: 150×20=3000(元)答:选择自助餐A需要2700元,选择自助餐B需要3000元。巧学妙记末尾有0数相乘,将0前数先对齐。再把0前数相乘,积的末尾再添0。 因数末尾有0的乘法的简便算法:先把0前面的数相乘,再看两个因数末尾一共有几个0,就在积的末尾添几个0。1 乘法第3课时 乘法的估算(教材P16)四年级数学·下 新课标[冀教] 第3单元估计一下:一个西瓜和一个哈密瓜,哪个重?(1)估算一下:这列火车大约有多少个座位?(2)算一算:这列火车实际有多少个座位?把因数看作与它接近的整十数或整百数进行估算。 方法一 118×12≈1200(个)
120×10=1200(个) 方法二 118×12≈1180(个)
118×10=1180(个)(1)118×12≈120×10=1200(个)(2)118×12=1416(个)巧学妙记乘法估算不用慌,四舍五入来帮忙。乘法估算并不难,凑十凑百来计算。1.估算时所得的结果是近似数,所以用“≈”。2.估算时把因数看成与它接近的整十数或整百数,计算比较简便。3.估算时把一个因数估大一些,另一个因数估小一些,它们的积更接近准确值。2 数量关系 (教材P18~21)四年级数学·下 新课标[冀教] 第3单元下面的购物小票中,你能看到哪些购物信息呢?读下面的发票,从中你了解到哪些信息?发票中的单价、数量、金额各表示什么? 理清单价、数量、金额的关系是解决此题的关键。 育才小学买了62套课桌椅,每套108元,一共花了6696元,还买了14个书柜,每个215元,一共花了3010元。
发票中的单价指的是每件的价钱,数量是买的件数,金额是一共花了多少钱,这三者的关系是:单价×数量=总价。总价÷数量=单价 总价÷单价=数量单价×数量=总价
总价÷数量=单价
总价÷单价=数量 单价、数量和总价三者的数量关系:
单价×数量=总价
总价÷数量=单价
总价÷单价=数量观察下面的铁路示意图。解答下面的问题:
(1)一列快速客车从北京发车,平均每小时行118千米,5小时行多少千米?
118×5= (千米)
(2)一列普通客车从北京出发,平均每小时行98千米,7小时行多少千米?
98×7= (千米) 火车每小时行的千米数称为速度,一共行驶的千米数,称为路程。 在速度、时间、路程三个量中,知道其中任意两个量,就可以求出第三个量。(1)(2)(1)118×5=590(千米) 答:5小时行590千米。(2)98×7=686(千米)答:7小时行686千米。 速度有一种特殊的表示方式,比如:快速列车平均每小时行118千米,记作118千米/时,读作118千米每时。速度、时间和路程三者之间的数量关系:
速度×时间=路程
路程÷时间=速度
路程÷速度=时间3 乘法运算律第1课时 乘法交换律和乘法结合律(教材P22~23)四年级数学·下 新课标[冀教] 第3单元以物换物,等价交换用计算器计算,并在圈里填上合适的符号。645×3232×64546×20353×180180×53203×46===乘法交换律与前边学过的加法交换律类似,不要混淆哦!= 乘法交换律:两个因数相乘,交换因数的位置,积不变。如果用a表示一个因数,b表示另一个因数,乘法交换律可以写成:a×b=b×a。一共有多少箱饮料?方法一×(6×5) × 4 = 120(箱)方法二 4 × (6×5) = 120(箱)规范解答(6×5)×4方法一方法二= 30×4= 120(箱)6×(5×4)= 6×20= 120(箱)答:一共有120箱饮料。答:一共有120箱饮料。巧学妙记乘法运算能简便,结合交换常做伴。连乘算式才适用,复杂计算变简单。 乘法结合律:三个数相乘,先乘前两个数或先乘后两个数,积不变。如果用a,b,c分别表示三个数,乘法结合律可以写成:(a×b)×c=a×(b×c)。3 乘法运算律第2课时 乘法分配律及简单应用(教材P24)四年级数学·下 新课标[冀教] 第3单元 植树节前,四(4)班的同学们去公园植树。1组20人,2组和3组都是10人。现在有60棵苗,怎么分配合理呢?两扇屏风一共有多少块玻璃?方法一(1)根据“排数×每排的块数”求出每一扇屏风上的玻璃数。(2)把两扇屏风上的玻璃数加起来就是一共的玻璃数。
12×5+9×5方法二(1)先求出两扇屏风每排的玻璃数。(2)再根据“每排的数量×排数”求出一共的玻璃数。(12+9)×5两种计算方法不同,但结果相等,即12×5+9×5=(12+9)×5。 乘法分配律是乘加或乘减两种运算之间的一种规律,而乘法交换律和乘法结合律只是乘法运算的一种规律方法一12×5+9×5=60+45=105(块)(12+9)×5=21×5=105(块)方法二答:两扇屏风一共有105块玻璃。巧学妙记乘法分配律好记,正能用来也能逆。乘加乘减才适用,计算简便是目的。1.两个数的和乘一个数,等于这两个数分别乘这个数,再把它们的积相加,这就叫做乘法分配律。
2.如果用a,b,c分别表示三个数,那么乘法分配律可以写成:(a+b)×c=a×c+b×c,也可以写成(a+b)c=ac+bc。3 乘法运算律第3课时 乘法的简便运算(教材P26~27)四年级数学·下 新课标[冀教] 第3单元 德国大数学家高斯在上小学时,有一天数学老师要求全班同学计算1+2+3+4+…
+99+100。高斯一会就算出答案是5050,而其他同学算到头昏脑涨也算不出来,最后只有高斯的答案正确无误。高斯的算法是:1+100=101,2+99=101,…,50+51=101,他是让前后两项两两相加,就组成了50对和都是101的配对,即101×50=5050。善于思考的高斯就是这样很快算出答案的。学校组织高年级102名师生去春游。(1)算一算:师生这次春游共需要多少元钱?
(2)102人中有4位老师,有98名学生。这些学生应交多少元钱?
(3)去春游的学生中,有36名是五年级的学生,五年级学生应交多少元钱?交钱人数×平均每人的费用=这些人一共交的钱数。(1) 102×25= (元)
100+2(2) 98×25= (元)
100-2(3) 25×36= (元)
4×9(1) 102×25= (100+2)×25= 100×25+2×25= 2500+50= 2550(元)答:师生这次春游共需要
2550元钱。(2) 98×25= (100-2)×25= 100×25-2×25= 2500-50= 2450(元)答:这些学生应交2450元钱。(3) 25×36= 25×(4×9)= 25×4×9= 100×9= 900(元)答:五年级学生应交900元钱。 两个数相乘,有时可以根据因数的特点,先将其中一个因数写成两个数相加(或相减)的形式,再将相加(或相减)的两个数分别与另一个因数相乘,最后把两个积相加(或相减)。 两个因数相乘时,可以把其中的一个因数看作两个数相加、相减或相乘的形式,然后直接用乘法运算定律进行计算,这样可以使计算变得简便。再 见
