冀教版数学四年级下册:第9单元 探索乐园-教学课件 31张PPT
文档属性
| 名称 | 冀教版数学四年级下册:第9单元 探索乐园-教学课件 31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 00:00:00 | ||
图片预览







文档简介
课件31张PPT。1 探索多边形中隐含的规律
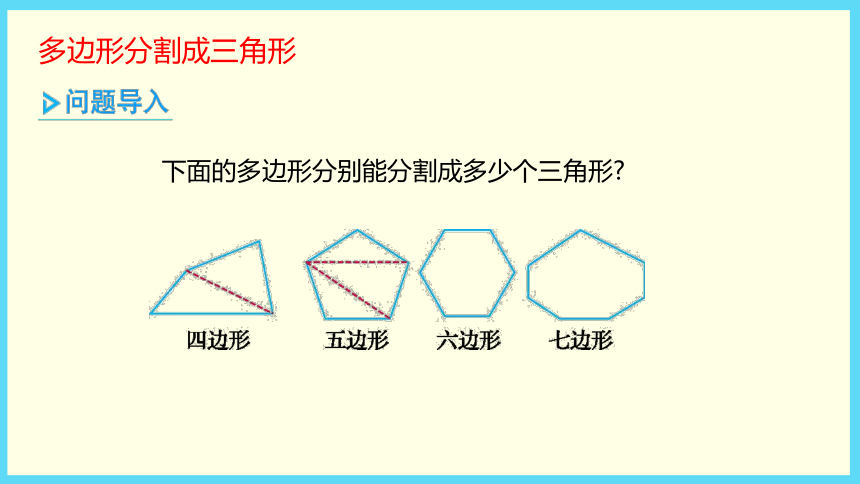
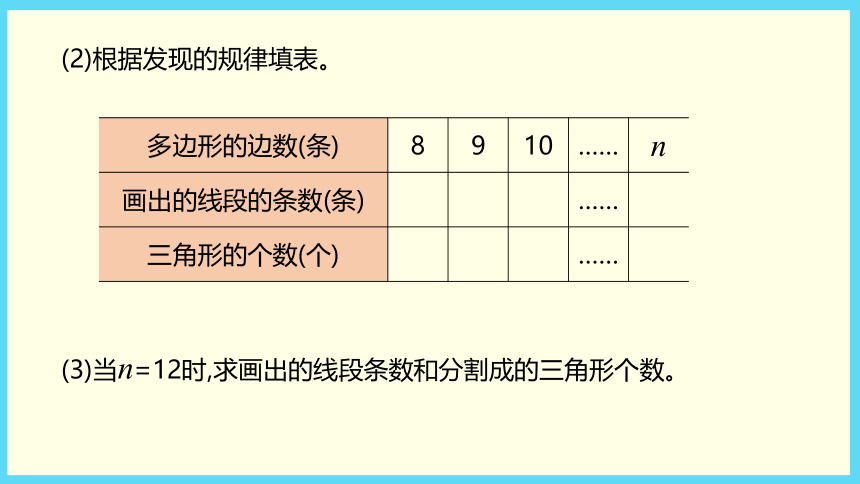
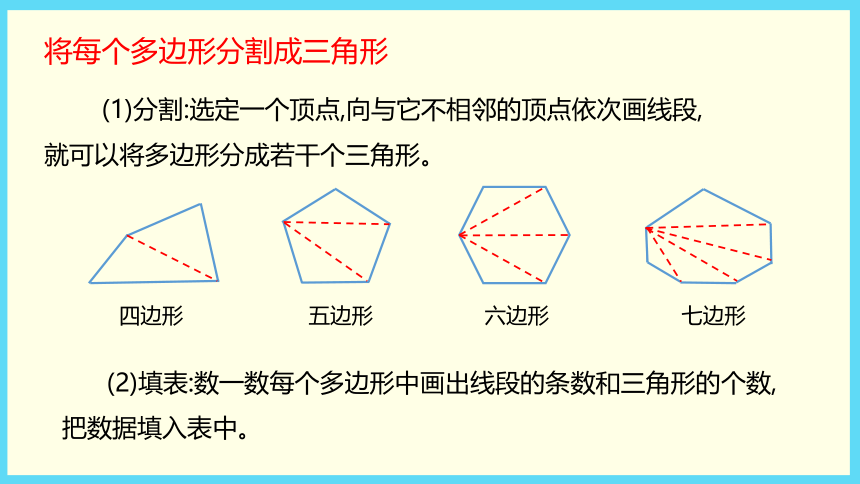
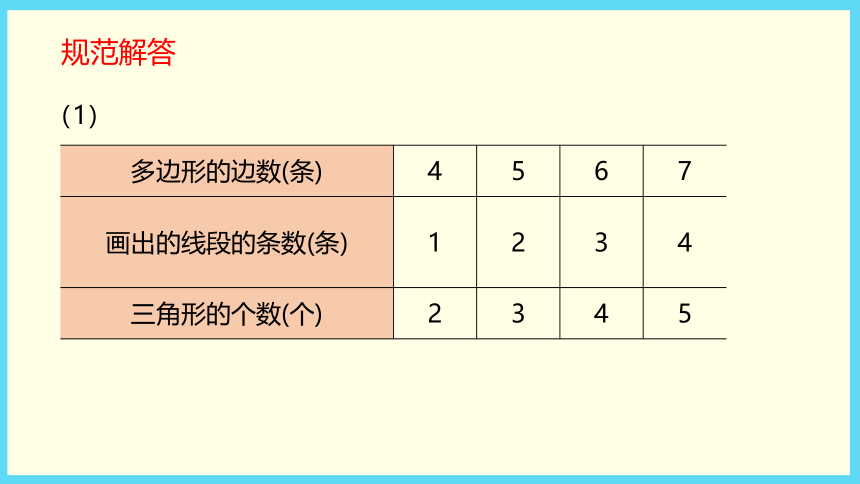
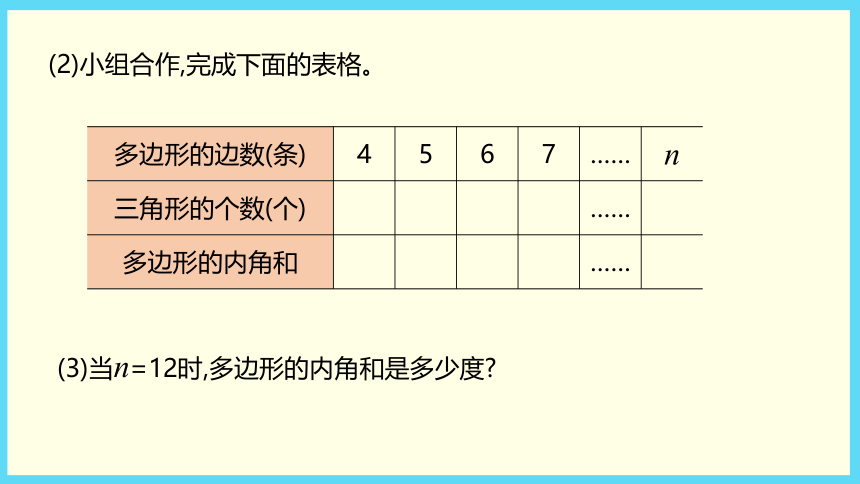
(教材P98~99)四年级数学·下 新课标[冀教] 第9单元多边形分割成三角形下面的多边形分别能分割成多少个三角形?(1)照样子画出虚线并填表。方法提示 选定一个顶点,向与它不相邻的顶点依次画线段,便可将多边形分割成若干个三角形。(2)根据发现的规律填表。(3)当n=12时,求画出的线段条数和分割成的三角形个数。理解题意一个图形由几条线段围成就是几边形。将多边形分别分割成三角形,并填表发现其中的规律。将每个多边形分割成三角形 (1)分割:选定一个顶点,向与它不相邻的顶点依次画线段,就可以将多边形分成若干个三角形。 (2)填表:数一数每个多边形中画出线段的条数和三角形的个数,把数据填入表中。发现规律并填表规范解答(1)(2)规范解答(3) 当n=12时,画出的线段的条数=n-3=12-3=9,分割成的三角形个数=n-2=12-2=10。从n边形的一个顶点出发,向与它不相邻的顶点连线段,画出的线段的条数是n-3(n≥4),分割成的三角形的个数是n-2(n≥4)。探索多边形边数和多边形内角和的关系多边形的内角和。(1)四边形的内角和是多少度?(2)小组合作,完成下面的表格。(3)当n=12时,多边形的内角和是多少度?理解题意求四边形的内角和是多少度,把四边形分割成两个三角形,一个三角形的内角和是180°,所以四边形的内角和为180°×2=360°。探究多边形的内角和规范解答(1)180°×2=360°(2)填表如下:(3)当n=12时,多边形的内角和是180°×(12-2)=1800°。以三角形为基础,每多一条边,内角和就增加180°n 边形的内角和是(n-2)×180°(n≥3)。2 探索组数中的规律
(教材P100~101)四年级数学·下 新课标[冀教] 第9单元探索由5个不同数字组成乘积最大或最小的三位数和两位数的方法用2,3,4,5,6五个数字组成一个三位数和一个两位数。
(1)怎样组数,可使两个数的乘积最大?
(2)要使两个数的乘积最小,该怎样组数?探究组三位数和两位数的方法(1)乘积最大。(2)乘积最小。总结规律(1)乘积最大组合。次大数中间数最小数最大数次小数(2)乘积最小组合。最小数中间数剩下数字组成
的最小三位数规范解答(1)乘积最大算式:542×63=34146(2)乘积最小算式:356×24=8544用5个数字(0除外)组成一个三位数和一个两位数,把5个数字按从大到小的顺序排列,最大的数要作为两位数的十位数,第4个数作为两位数的个位数,其他3个数字组成最大的三位数,这时乘积最大。把5个数字从小到大排序,最小的数作为两位数的十位数,第3个数作为两位数的个位数,其他3个数字组成最小的三位数,这时乘积最小。探索积的规律(1)用计算器计算,看看积有什么规律。(2)利用发现的规律写出下面两道题的得数。11111111×11111111= 111111111×111111111=理解题意 用计算器计算出前五个算式的积,找出规律,利用发现的规律直接写出后面两道题的得数。用计算器计算1121123211234321123454321探索规律1111 × 1111 =1 2 3 4 3 2 111111111×11111111 =111111111×111111111 =12345678987654321123456787654321规范解答从简单问题分析特点,找到规律,再根据总结出的规律解决复杂问题。再 见
(教材P98~99)四年级数学·下 新课标[冀教] 第9单元多边形分割成三角形下面的多边形分别能分割成多少个三角形?(1)照样子画出虚线并填表。方法提示 选定一个顶点,向与它不相邻的顶点依次画线段,便可将多边形分割成若干个三角形。(2)根据发现的规律填表。(3)当n=12时,求画出的线段条数和分割成的三角形个数。理解题意一个图形由几条线段围成就是几边形。将多边形分别分割成三角形,并填表发现其中的规律。将每个多边形分割成三角形 (1)分割:选定一个顶点,向与它不相邻的顶点依次画线段,就可以将多边形分成若干个三角形。 (2)填表:数一数每个多边形中画出线段的条数和三角形的个数,把数据填入表中。发现规律并填表规范解答(1)(2)规范解答(3) 当n=12时,画出的线段的条数=n-3=12-3=9,分割成的三角形个数=n-2=12-2=10。从n边形的一个顶点出发,向与它不相邻的顶点连线段,画出的线段的条数是n-3(n≥4),分割成的三角形的个数是n-2(n≥4)。探索多边形边数和多边形内角和的关系多边形的内角和。(1)四边形的内角和是多少度?(2)小组合作,完成下面的表格。(3)当n=12时,多边形的内角和是多少度?理解题意求四边形的内角和是多少度,把四边形分割成两个三角形,一个三角形的内角和是180°,所以四边形的内角和为180°×2=360°。探究多边形的内角和规范解答(1)180°×2=360°(2)填表如下:(3)当n=12时,多边形的内角和是180°×(12-2)=1800°。以三角形为基础,每多一条边,内角和就增加180°n 边形的内角和是(n-2)×180°(n≥3)。2 探索组数中的规律
(教材P100~101)四年级数学·下 新课标[冀教] 第9单元探索由5个不同数字组成乘积最大或最小的三位数和两位数的方法用2,3,4,5,6五个数字组成一个三位数和一个两位数。
(1)怎样组数,可使两个数的乘积最大?
(2)要使两个数的乘积最小,该怎样组数?探究组三位数和两位数的方法(1)乘积最大。(2)乘积最小。总结规律(1)乘积最大组合。次大数中间数最小数最大数次小数(2)乘积最小组合。最小数中间数剩下数字组成
的最小三位数规范解答(1)乘积最大算式:542×63=34146(2)乘积最小算式:356×24=8544用5个数字(0除外)组成一个三位数和一个两位数,把5个数字按从大到小的顺序排列,最大的数要作为两位数的十位数,第4个数作为两位数的个位数,其他3个数字组成最大的三位数,这时乘积最大。把5个数字从小到大排序,最小的数作为两位数的十位数,第3个数作为两位数的个位数,其他3个数字组成最小的三位数,这时乘积最小。探索积的规律(1)用计算器计算,看看积有什么规律。(2)利用发现的规律写出下面两道题的得数。11111111×11111111= 111111111×111111111=理解题意 用计算器计算出前五个算式的积,找出规律,利用发现的规律直接写出后面两道题的得数。用计算器计算1121123211234321123454321探索规律1111 × 1111 =1 2 3 4 3 2 111111111×11111111 =111111111×111111111 =12345678987654321123456787654321规范解答从简单问题分析特点,找到规律,再根据总结出的规律解决复杂问题。再 见
