苏教版高中数学选修数学选修2-2《数系的扩充》课件(共34张PPT)
文档属性
| 名称 | 苏教版高中数学选修数学选修2-2《数系的扩充》课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 09:24:54 | ||
图片预览









文档简介
(共34张PPT)
问题情境
问题1:将10分成两数,使两者的乘积等于40,求这两数.
数系的扩充与复数的引入
数系的扩充
教学目标:
1.经历数的概念的发展和数系扩充的过程,体会数学发现和创
造的过程,以及数学发生,发展的客观需求.
2.理解复数的基本概念以及复数相等的条件.
问题一:
阅读课本,思考:数系的扩充经历了哪两条路线?它们的历程分别是什么?
数系的扩充
创设情景,探究问题
自然数
因计数的需要
生活和生产实践的需要
数系的扩充
创设情景,探究问题
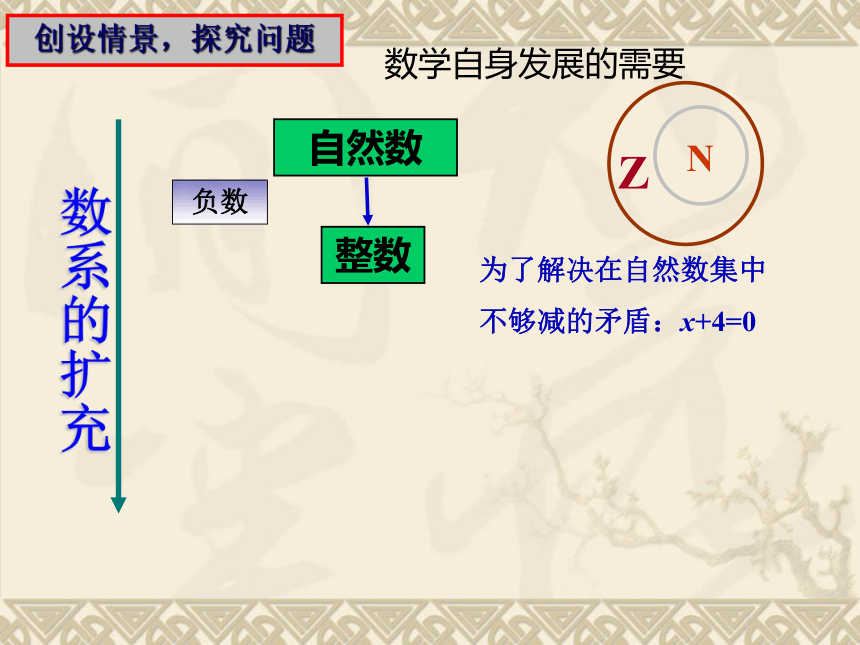
自然数
为了解决在自然数集中
不够减的矛盾:x+4=0
Z
负数
数学自身发展的需要
数系的扩充
创设情景,探究问题
自然数
Z
负数
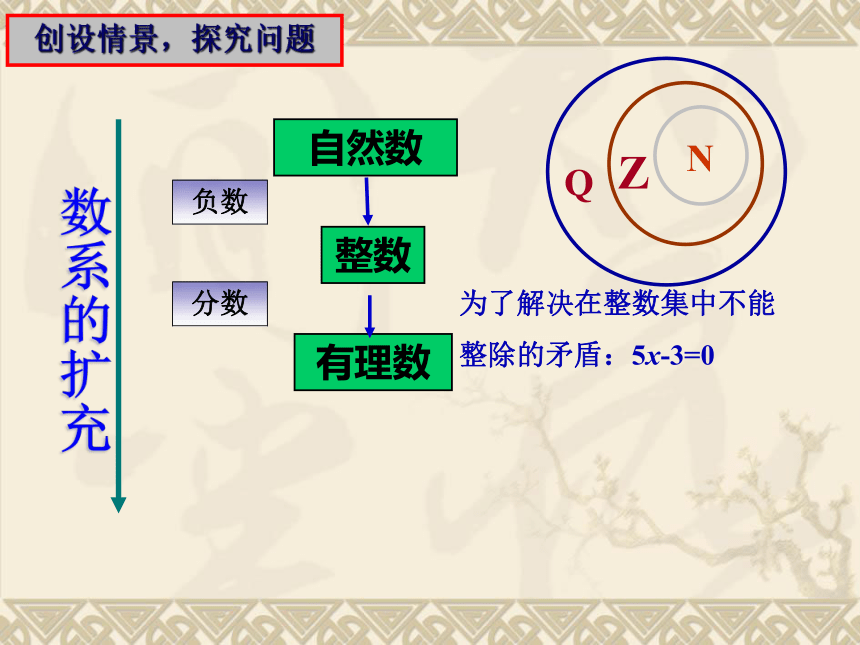
为了解决在整数集中不能
整除的矛盾:5x-3=0
分数
Q
C
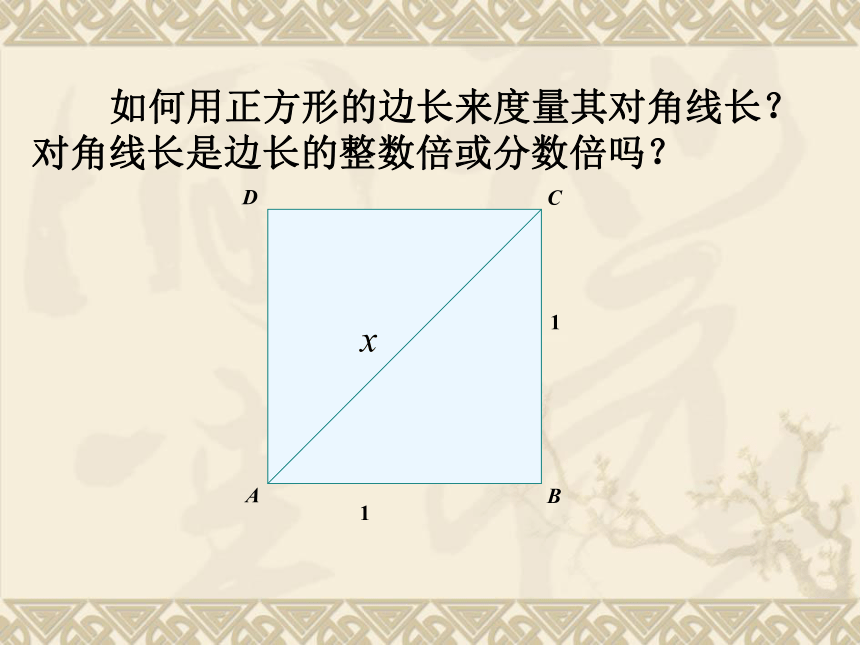
如何用正方形的边长来度量其对角线长?对角线长是边长的整数倍或分数倍吗?
数系的扩充
创设情景,探究问题
自然数
实数
Z
负数
分数
Q
为了解决正数开方开不尽
的矛盾:x2=2
无理数
R
第一次数学危机:无理数的产生
古希腊的毕达哥拉斯学派认为, 世间任何数都可以用整数或分数表示,并将此作为他们的信条.
有一天,这个学派中的一个成员希伯斯突然发现:边长为1的正方形的对角线是个奇怪的数,于是努力研究,终于证明出它不能用整数或分数表示.
这一发现打破了毕达哥拉斯学派的信条,于是毕达哥拉斯命令他不许外传,但希伯斯却将这一秘密透露了出去.毕达哥拉斯大怒,下令将他处死.希伯斯连忙外逃,然而还是被抓住了,被扔入了大海,为科学的发展献出了宝贵的生命.
希伯斯发现的这类数,被称为无理数.无理数的发现,导致了第一次数学危机,为数学的发展做出了重大贡献.
历史链接
数系的扩充
创设情景,探究问题
自然数
实数
Z
负数
分数
Q
无理数
R
?
方程x2+1=0在实数集内无解,负数不能开平方
学生活动
现在我们要进行数系的再
一次扩充就是要解决什么
问题? 怎么解决?
讨论
你能给出一个解决问题的方 案吗?
问题2:
实系数一元二次方程 在实数集范围内无解.
我们能否将实数集进行扩充,使得它在新的数集中,该问题能得到圆满解决呢?
引入一个新数:
合情推理,类比扩充
我们就引入这样一个新数 i ,把 i 叫做虚数单位,并且规定:
引入新数,完善数系
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.
(1)i2??1;
数系的扩充
创设情景,探究问题
自然数
实数
负数
分数
无理数
虚数
复数
阅读课本,思考:
1.复数的定义?
2.复数的代数形式?
复数: 把形如a+bi(a,b∈R)的数叫做复数.
复数集: 全体复数所形成的集合叫做复数集,
一般用大写字母C表示 .
实部
复数的代数形式:
复数通常用字母 z 表示,即
虚部
其中i称为虚数单位.
引入新数,完善数系
引入新数,完善数系
复数集,虚数集,实数集,纯虚数集之间的关系?
复数
虚数
实数
纯虚数
1.指出下列复数的实部与虚部.
即时训练,巩固新知
上述复数中,实数有 ; 虚数有 ; 纯虚数有 .(填上所有你认为正确的序号)
2.判断下列命题是否正确:
(1)若a、b为实数,则 z=a+bi为虚数;
(2)若b为实数,则z=bi必为纯虚数;
(3)若a为实数,则z= a一定不是虚数.
即时训练,巩固新知
例题分析
实数m取什么值时,复数z=m(m-1)+(m-1)i是
(1)实数? (2)虚数? (3)纯虚数?
分析:由m∈R可知m-1, m(m-1)是实数,根据复数z= a+bi是实数,虚数和纯虚数的条件可分别确定m的值.
复数 是纯虚数,则实数m= ;
变式训练
变式:若m是纯虚数,则上述复数z的虚部是= .
如何定义两个复数的相等?
注意:一般对两个复数只能说相等或不相等;不能比较大小;当且仅当两复数都是实数时,才可比较大小.
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
探究思考
复数相等的问题
转化
实数集中求方程组的解的问题
一种重要的数学思想:方程思想
例题分析
已知复数z1= (x + y) + (x-2y)i ,复数z2 = (2x-5) + (3x+y)i,若z1 = z2 ,求实数x,y的值.
变式1:若上述复数z1∈{5},求实数x,y的值.
变式2:若上述复数z1≠ z2 ,求实数应x,y满足的条件.
变式3:若上述复数z1>0,复数z2和纯虚数z3相等 ,求实数x,y的值.
1.数的概念的发展及数系的扩充过程;
2.复数的有关概念;
3.复数相等的充要条件.
归纳总结
辨析:
1.已知:i是虚数单位,实数m取什么值时,复数
是(1)实数; (2)虚数;
(3)纯虚数; (4)零.
2.设i是虚数单位, 若 ,求实数 的值.
思考1
思考2
思考3
思考4
设M是一个非空集合,f是一种运算.如果对于集合M
中任意两个元素p,q,实施运算f的结果仍是集合M中的
元素,那么就说集合M对于运算f是封闭的.已知集合
M = {x|x = a + b ,a,b∈Q},试验证集合M对于加法、
减法、乘法和除法(除数不为0)运算是封闭的.
问题情境
问题1:将10分成两数,使两者的乘积等于40,求这两数.
数系的扩充与复数的引入
数系的扩充
教学目标:
1.经历数的概念的发展和数系扩充的过程,体会数学发现和创
造的过程,以及数学发生,发展的客观需求.
2.理解复数的基本概念以及复数相等的条件.
问题一:
阅读课本,思考:数系的扩充经历了哪两条路线?它们的历程分别是什么?
数系的扩充
创设情景,探究问题
自然数
因计数的需要
生活和生产实践的需要
数系的扩充
创设情景,探究问题
自然数
为了解决在自然数集中
不够减的矛盾:x+4=0
Z
负数
数学自身发展的需要
数系的扩充
创设情景,探究问题
自然数
Z
负数
为了解决在整数集中不能
整除的矛盾:5x-3=0
分数
Q
C
如何用正方形的边长来度量其对角线长?对角线长是边长的整数倍或分数倍吗?
数系的扩充
创设情景,探究问题
自然数
实数
Z
负数
分数
Q
为了解决正数开方开不尽
的矛盾:x2=2
无理数
R
第一次数学危机:无理数的产生
古希腊的毕达哥拉斯学派认为, 世间任何数都可以用整数或分数表示,并将此作为他们的信条.
有一天,这个学派中的一个成员希伯斯突然发现:边长为1的正方形的对角线是个奇怪的数,于是努力研究,终于证明出它不能用整数或分数表示.
这一发现打破了毕达哥拉斯学派的信条,于是毕达哥拉斯命令他不许外传,但希伯斯却将这一秘密透露了出去.毕达哥拉斯大怒,下令将他处死.希伯斯连忙外逃,然而还是被抓住了,被扔入了大海,为科学的发展献出了宝贵的生命.
希伯斯发现的这类数,被称为无理数.无理数的发现,导致了第一次数学危机,为数学的发展做出了重大贡献.
历史链接
数系的扩充
创设情景,探究问题
自然数
实数
Z
负数
分数
Q
无理数
R
?
方程x2+1=0在实数集内无解,负数不能开平方
学生活动
现在我们要进行数系的再
一次扩充就是要解决什么
问题? 怎么解决?
讨论
你能给出一个解决问题的方 案吗?
问题2:
实系数一元二次方程 在实数集范围内无解.
我们能否将实数集进行扩充,使得它在新的数集中,该问题能得到圆满解决呢?
引入一个新数:
合情推理,类比扩充
我们就引入这样一个新数 i ,把 i 叫做虚数单位,并且规定:
引入新数,完善数系
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.
(1)i2??1;
数系的扩充
创设情景,探究问题
自然数
实数
负数
分数
无理数
虚数
复数
阅读课本,思考:
1.复数的定义?
2.复数的代数形式?
复数: 把形如a+bi(a,b∈R)的数叫做复数.
复数集: 全体复数所形成的集合叫做复数集,
一般用大写字母C表示 .
实部
复数的代数形式:
复数通常用字母 z 表示,即
虚部
其中i称为虚数单位.
引入新数,完善数系
引入新数,完善数系
复数集,虚数集,实数集,纯虚数集之间的关系?
复数
虚数
实数
纯虚数
1.指出下列复数的实部与虚部.
即时训练,巩固新知
上述复数中,实数有 ; 虚数有 ; 纯虚数有 .(填上所有你认为正确的序号)
2.判断下列命题是否正确:
(1)若a、b为实数,则 z=a+bi为虚数;
(2)若b为实数,则z=bi必为纯虚数;
(3)若a为实数,则z= a一定不是虚数.
即时训练,巩固新知
例题分析
实数m取什么值时,复数z=m(m-1)+(m-1)i是
(1)实数? (2)虚数? (3)纯虚数?
分析:由m∈R可知m-1, m(m-1)是实数,根据复数z= a+bi是实数,虚数和纯虚数的条件可分别确定m的值.
复数 是纯虚数,则实数m= ;
变式训练
变式:若m是纯虚数,则上述复数z的虚部是= .
如何定义两个复数的相等?
注意:一般对两个复数只能说相等或不相等;不能比较大小;当且仅当两复数都是实数时,才可比较大小.
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
探究思考
复数相等的问题
转化
实数集中求方程组的解的问题
一种重要的数学思想:方程思想
例题分析
已知复数z1= (x + y) + (x-2y)i ,复数z2 = (2x-5) + (3x+y)i,若z1 = z2 ,求实数x,y的值.
变式1:若上述复数z1∈{5},求实数x,y的值.
变式2:若上述复数z1≠ z2 ,求实数应x,y满足的条件.
变式3:若上述复数z1>0,复数z2和纯虚数z3相等 ,求实数x,y的值.
1.数的概念的发展及数系的扩充过程;
2.复数的有关概念;
3.复数相等的充要条件.
归纳总结
辨析:
1.已知:i是虚数单位,实数m取什么值时,复数
是(1)实数; (2)虚数;
(3)纯虚数; (4)零.
2.设i是虚数单位, 若 ,求实数 的值.
思考1
思考2
思考3
思考4
设M是一个非空集合,f是一种运算.如果对于集合M
中任意两个元素p,q,实施运算f的结果仍是集合M中的
元素,那么就说集合M对于运算f是封闭的.已知集合
M = {x|x = a + b ,a,b∈Q},试验证集合M对于加法、
减法、乘法和除法(除数不为0)运算是封闭的.
