人教版七年级数学下册 第五章 平行线的性质和判定 基础练习(PDF版 含答案)
文档属性
| 名称 | 人教版七年级数学下册 第五章 平行线的性质和判定 基础练习(PDF版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 755.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 20:12:35 | ||
图片预览


文档简介
人教版七年级
平行线的性质和判定基础练习(含答案)
一、单选题(共有 11 道小题)
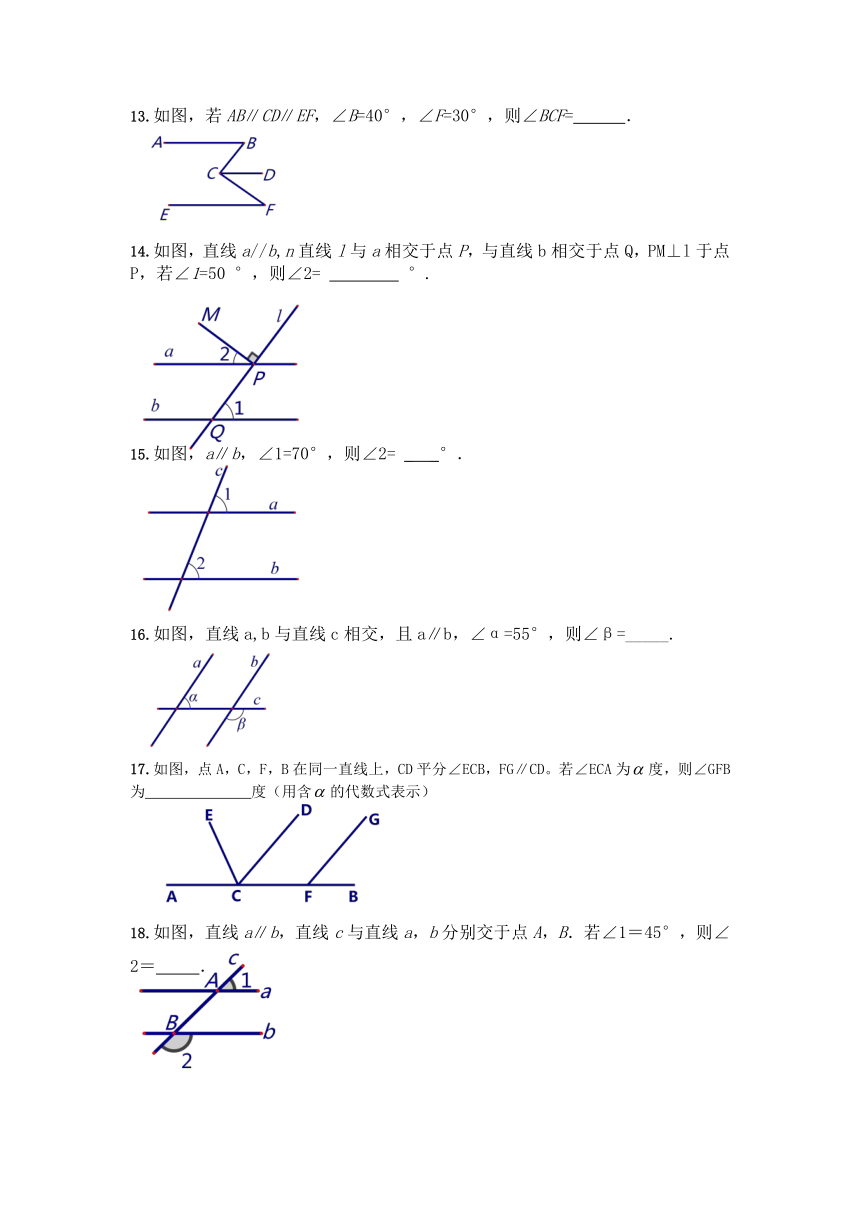
1.如图,含 30°角的直角三角尺 DEF 放置在△ABC 上,30°角的顶点 D在边 AB 上,DE⊥AB,
若∠B为锐角,BC∥DF,则∠B 的大小为( )
A.30° B. 45° C. 60° D.75°
2.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D 的大小为( )
A.65° B.55° C.45° D.35°
3.如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
4.如图,直线 a∥b,直角三角板(含 30°角)如图放置,∠DCB=90°,若∠1
+∠B=70°,则∠2的度数为( )
A.20° B.40° C.30° D.25°
5.如图,直线 l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A. 30° B. 35° C. 36° D. 40°
6.下列说法不正确...是( )
A.两直线平行,同位角相等
B.两点之间直线最短
C.对顶角相等
D.半圆所对的圆周角是直角
7.如图,AD 是∠EAC 的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
8.如图,已知直线 a∥b,∠1=131°,则∠2等于( )
A.39° B.41° C.49° D.59°
9.如图,直线 a与直线 b交于点 A,与直线 c 交于点 B,∠1=120°,∠2=45°,
若使直线 b与直线 c平行,则可将直线 b绕点 A逆时针旋转( )
A.15° B. 30° C. 45° D.60°
10.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为
( )
A.60° B.50° C.40° D.30°
11.如图,已知 AB∥CD,∠C=65°,∠E=30°,则∠A的度数为( )
A.30° B.32.5° C.35° D.37.5°
二、填空题(共有 10 道小题)
12.如图,AB // CD,BC 与 AD 相交于点 M,N 是射线 CD 上的一点。若∠B = 65°,∠MDN =
135°,则∠AMB = ________。
13.如图,若 AB∥CD∥EF,∠B=40°,∠F=30°,则∠BCF= .
14.如图,直线 a//b,n 直线 l与 a相交于点 P,与直线 b相交于点 Q,PM⊥l 于点
P,若∠1=50 °,则∠2= °.
15.如图,a∥b,∠1=70°,则∠2= _ _°.
16.如图,直线 a,b 与直线 c相交,且 a∥b,∠α=55°,则∠β=_____.
17.如图,点 A,C,F,B在同一直线上,CD 平分∠ECB,FG∥CD。若∠ECA 为? 度,则∠GFB
为 度(用含? 的代数式表示)
18.如图,直线 a∥b,直线 c与直线 a,b分别交于点 A,B.若∠1=45°,则∠
2= .
19.如图,直线 1 2l l? , ? ?? ? ? ,∠1=40°,则∠2=
20.如图,直线 a∥b,直线 a、b被直线 c所截,∠1=37°,则∠2=
21.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是___.
三、解答题(共有 3道小题)
22.如图,EF ∥ BC , AC 平分 BAF? , 80B? ? ?.求 C? 的度数.
23.如图,直线 a∥b,点 B在直线 b上,且 AB⊥BC,∠1=55°,求∠2的度数.
24.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°. 求证:AB∥CD.
参考答案
一、单选题(共有 11 道小题)
1.C
2.B
3.D
4.A
5.A
6.B
7.A
8.C
9.A
10.A
11.C
二、填空题(共有 10 道小题)
12.70°
13.70
14.40
15.70
16.125°
17.
190
2
??
18.135°.
19.140°
20.143°
21.55°
三、解答题(共有 3道小题)
22.解:∵ EF ∥ BC ,
∴ 180 100BAF B? ? ? ?? ? ?
∵ AC 平分 BAF? ,
∴
1 50
2
CAF BAF? ? ? ? ?
∵ EF ∥ BC ,
∴ 50C CAF? ? ? ? ? .
23.解:∵AB⊥BC,
∴∠1+∠3=90°
∵∠1=55°
∴∠3=35°
∵a∥b,
∴∠2=∠3=35°
24.证明:
∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
平行线的性质和判定基础练习(含答案)
一、单选题(共有 11 道小题)
1.如图,含 30°角的直角三角尺 DEF 放置在△ABC 上,30°角的顶点 D在边 AB 上,DE⊥AB,
若∠B为锐角,BC∥DF,则∠B 的大小为( )
A.30° B. 45° C. 60° D.75°
2.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D 的大小为( )
A.65° B.55° C.45° D.35°
3.如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
4.如图,直线 a∥b,直角三角板(含 30°角)如图放置,∠DCB=90°,若∠1
+∠B=70°,则∠2的度数为( )
A.20° B.40° C.30° D.25°
5.如图,直线 l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A. 30° B. 35° C. 36° D. 40°
6.下列说法不正确...是( )
A.两直线平行,同位角相等
B.两点之间直线最短
C.对顶角相等
D.半圆所对的圆周角是直角
7.如图,AD 是∠EAC 的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
8.如图,已知直线 a∥b,∠1=131°,则∠2等于( )
A.39° B.41° C.49° D.59°
9.如图,直线 a与直线 b交于点 A,与直线 c 交于点 B,∠1=120°,∠2=45°,
若使直线 b与直线 c平行,则可将直线 b绕点 A逆时针旋转( )
A.15° B. 30° C. 45° D.60°
10.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为
( )
A.60° B.50° C.40° D.30°
11.如图,已知 AB∥CD,∠C=65°,∠E=30°,则∠A的度数为( )
A.30° B.32.5° C.35° D.37.5°
二、填空题(共有 10 道小题)
12.如图,AB // CD,BC 与 AD 相交于点 M,N 是射线 CD 上的一点。若∠B = 65°,∠MDN =
135°,则∠AMB = ________。
13.如图,若 AB∥CD∥EF,∠B=40°,∠F=30°,则∠BCF= .
14.如图,直线 a//b,n 直线 l与 a相交于点 P,与直线 b相交于点 Q,PM⊥l 于点
P,若∠1=50 °,则∠2= °.
15.如图,a∥b,∠1=70°,则∠2= _ _°.
16.如图,直线 a,b 与直线 c相交,且 a∥b,∠α=55°,则∠β=_____.
17.如图,点 A,C,F,B在同一直线上,CD 平分∠ECB,FG∥CD。若∠ECA 为? 度,则∠GFB
为 度(用含? 的代数式表示)
18.如图,直线 a∥b,直线 c与直线 a,b分别交于点 A,B.若∠1=45°,则∠
2= .
19.如图,直线 1 2l l? , ? ?? ? ? ,∠1=40°,则∠2=
20.如图,直线 a∥b,直线 a、b被直线 c所截,∠1=37°,则∠2=
21.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是___.
三、解答题(共有 3道小题)
22.如图,EF ∥ BC , AC 平分 BAF? , 80B? ? ?.求 C? 的度数.
23.如图,直线 a∥b,点 B在直线 b上,且 AB⊥BC,∠1=55°,求∠2的度数.
24.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°. 求证:AB∥CD.
参考答案
一、单选题(共有 11 道小题)
1.C
2.B
3.D
4.A
5.A
6.B
7.A
8.C
9.A
10.A
11.C
二、填空题(共有 10 道小题)
12.70°
13.70
14.40
15.70
16.125°
17.
190
2
??
18.135°.
19.140°
20.143°
21.55°
三、解答题(共有 3道小题)
22.解:∵ EF ∥ BC ,
∴ 180 100BAF B? ? ? ?? ? ?
∵ AC 平分 BAF? ,
∴
1 50
2
CAF BAF? ? ? ? ?
∵ EF ∥ BC ,
∴ 50C CAF? ? ? ? ? .
23.解:∵AB⊥BC,
∴∠1+∠3=90°
∵∠1=55°
∴∠3=35°
∵a∥b,
∴∠2=∠3=35°
24.证明:
∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
