1.1.1 等腰三角形的性质课件

(共17张PPT)
数学北师大版

八年级
1.1.1 等腰三角形
第1课时等腰三角形的性质

名称 图 形 性 质
等
腰
三
角
形 边
角
顶角平分线
底边中线
底边高线
对称性
两底角相等
三线合一
两腰相等
轴对称图形
问题1.找出下列条件中能判定两个三角形全等的是：①SSS，②SAS，③ASA，④AAA，⑤SSA，⑥AAS。
问题2.两角分别相等且其中一组等角的对边相等的两个三角形全等（AAS）?你能你能证明它吗？
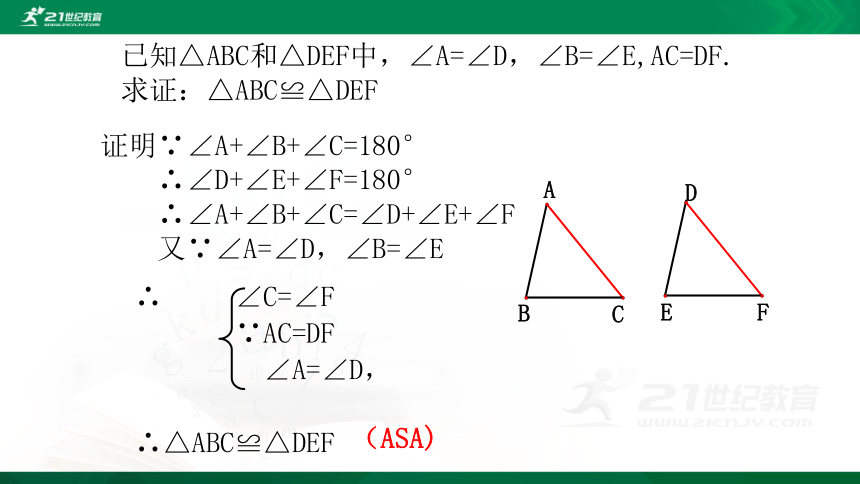
已知△ABC和△DEF中，∠A=∠D，∠B=∠E,AC=DF.求证：△ABC≌△DEF





∴ ∠C=∠F
∵AC=DF
∠A=∠D，

∴△ABC≌△DEF
已知△ABC和△DEF中，∠A=∠D，∠B=∠E,AC=DF.求证：△ABC≌△DEF
（ASA)

证明∵∠A+∠B+∠C=180°
　　∴∠D+∠E+∠F=180°
　　∴∠A+∠B+∠C=∠D+∠E+∠F
又∵∠A=∠D，∠B=∠E
定理：两角分别相等且其中一组等角的对边相等的
两个三角形全等.（AAS)
根据全等三角形的定义，就得到：全等三角形的对应
边相等，对应角相等.
请证明定理:等腰三角形的两底角相等.(等边对等角)

B
C
A
已知：△ABC中，AB=AC，求证：∠B=∠C.


证明：取BC的中点D，连接AD。
∵AB＝AC，BD＝CD，AD＝AD，
∴△ABC≌△ACD (SSS)
∴∠B=∠C (全等三角形的对应边角相等)
当△ABD≌△ACD时，线段AD还有怎样的性质？
为什么？
⑴当△ABD≌△ACD时，∠BAD=∠CAD，则AD是顶角∠BAC的平分线。
⑵当△ABD≌△ACD时，∠BDA=∠CDA， 因为∠BDA+∠CDA=180O ，所以∠BDA=∠CDA=90O，那么AD⊥BC，则AD是△ABC的底边上的中线。

D
(AD是底边上的中线)
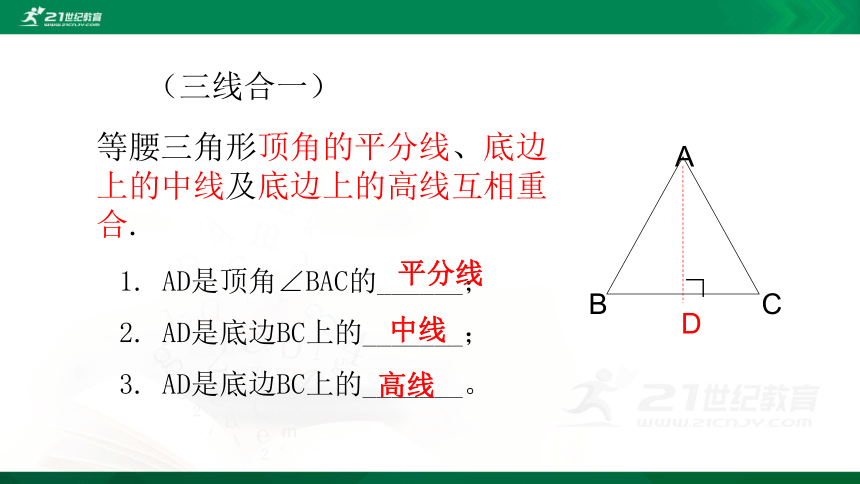
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.

B
C
A

∟
D
（三线合一）
1. AD是顶角∠BAC的______；
2. AD是底边BC上的_______；
3. AD是底边BC上的_______。
平分线
中线
高线
等腰三角形的性质
证法二：
证明：作∠ BAC的角平分线AD 交 BC于点D.
在△ABD 和△ACD 中
∵ AB=AC , ∠BAD =∠CAD , AD = AD
∴ △ABD ≌ △ACD (SAS)
∴ ∠B=∠C （全等三角形的对应角相等）

定理: 等腰三角形的两个底角相等. (等边对等角)

A
C
B

D
如图，在ΔABC中，AB＝AC
求证：∠B＝∠C
定理:
等腰三角形的两个底角相等(等边对等角).


A
C

B
已知:
如图,在△ABC中, AB=AC.
求证: ∠B=∠C.
在Rt△ABD与Rt△ACD中
∵ AB=AC
AD=AD
∴ Rt △ABD≌ Rt △ACD（HL）.



D
证法三：
证明:过点A作AD⊥BC,交BC于点D.
∴ ∠B=∠C（全等三角形的对应角相等）.

例.△ABC中，AB＝AC，D是BC边上的中点，
DF⊥AC于F DE ⊥ AB 于E
求证：DE＝DF。



A
B
C

D


E
F




证明：
∵DE⊥AB，DF⊥AC
∴∠BED＝∠CFD
又∵D是BC中点（已知）
∴BD＝DC
∵AB＝AC（已知）
∴∠B＝∠C（等边对等角）

在△DBE与△DCF中
∠DEB＝∠DFC（已证）
∠B＝∠C（已证）
BD＝DC（已证）
∴ △BDE ≌ △CDF（AAS）
∴DE＝DF
方法二：连AD 。
∵AB＝AC，BD＝DC（已知）
∴AD是∠BAC的平分线。
（等腰三角形三线合一）
又∵DE⊥AB DF⊥AC
∴DE＝DF（角平分线上的点到这个角的两边距离相等）



A
B
C

D


E
F




例.△ABC中，AB＝AC，D是BC边上的中点，
DF⊥AC于F DE ⊥ AB 于E .求证：DE＝DF。
1．在 △ABC 中，AB = AC.
（1）若 ∠ A = 40°，则 ∠ C 等于 度.
（2）若 ∠ B = 72°，则 ∠ A 等于 度.
（3）若有一内角为40°，则另外两个内角分别
是 .
2． 如图，在 △ABC 中，∠ BAC = 108°，
AB = AC，AD⊥ BC，垂足为 D，
则∠BAD等于 度。
70
70°和70°
36
或40°和100°
54
随堂练习
3．(10分)如图，在△ABC中，AB＝AC，AD⊥BC，CE⊥AB，
AE＝CE.
求证：(1)△AEF≌△CEB；
(2)AF＝2CD.
证明：(1)∵AD⊥BC，∴∠B＋∠BAD＝90°，∵CE⊥AB， ∴∠B＋∠BCE＝90°，∴∠EAF＝∠ECB， 在△AEF和△CEB中，
∠EAF＝∠ECB，
AE＝CE，
∠AEF＝∠CEB
∴△AEF≌△CEB

(2)∵△AEF≌△CEB，∴AF＝BC，
∵AB＝AC，AD⊥BC，
∴CD＝BD，∴BC＝2CD，∴AF＝2CD











小结：
1.定理：（AAS)
2.全等三角形的性质：
全等三角形的对应边相等，对应角相等.
3.等腰三角形的性质：
等腰三角形的两底角相等.
4.等腰三角形性质的推论：（三线合一）
等腰三角形顶角的平分线、底边上的中线及底边上的高
互相重合.
两角分别相等且其中一组等角的对边相等的两个三角形全等.
课外作业. 如图,在△ABD中,C是BD上的一点，且AC⊥BD，AC=BC=CD，
（1）求证： △ABD是等腰三角形;
（2）求∠BAD的度数.
解：（1）∵AC⊥BD，AC=BC=CD，

∴∠ACB=∠ACD=90°．

∴△ACB≌△ACD．

∴AB=AD．

∴△ABD是等腰三角形．

（2）∵AC⊥BD，AC=BC=CD，

∴△ACB、△ACD都是等腰直角三角形．

∴∠B=∠D=45°．

∴∠BAD=90°．
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php