2020年湖南省普通高中学业水平考试数学模拟试题
文档属性
| 名称 | 2020年湖南省普通高中学业水平考试数学模拟试题 |  | |
| 格式 | zip | ||
| 文件大小 | 122.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 22:18:46 | ||
图片预览



文档简介
2020年湖南省普通高中学业水平考试数学模拟试题
一、选择题:(本大题共10小题,每小题4分,共40分)
1.如图是一个几何体的三视图,则该几何体为(
)
A.球
B.圆柱
C.圆台
D.圆锥
2.下列命题正确的是(
)
A.如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
B.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
C.垂直于同一条直线的两条直线相互垂直
D.若两条直线与第三条直线所成的角相等,则这两条直线互相平行
3、如右图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为(
)
A、6+
B、24+
C、24+2
D、32
4.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是(
)
A.
B.
C.
D.
5.
已知直线:和圆C:
,则直线和圆C的位置关系为(
).
A.相交
B.
相切
C.相离
D.
不能确定
6、直线的倾斜角为(
)
A、300
B、600
C、1200
D、1500
7.直线与圆没有公共点,则的取值范围是(
)
A.
B.
C.
D.
8.已知直线与直线平行,则的值为
(
)
A.
B.
C.
D.
9、直线2x+y+5=0上的点到原点距离的最小值为
(
)
A.
B.
C.
D.
10.互相垂直,则的值是
A.
-3
B.
0
C.
0或-3
D.
0或1
2、填空题:(本大题共5小题,每小题4分,共20分)
11.直线的斜率是
,在轴的截距为
12.
已知直线过点(0,7),且与直线垂直,则直线的方程为
13.经过圆的圆心,且与直线平行的直线方程是
.
14.已知圆C:=4及直线l:x-y+3=0,则直线被C截得的弦长为
15.设有四个条件:①平面与平面、所成的锐二面角相等;②直线a//b,a⊥平面,b⊥平面;③a、b是异面直线,a,b,且a//,b//;④平面内距离为d的两条直线在平面内的射影仍为两条距离为d的平行线。
其中能推出//的条件有
。(填写所有正确条件的代号)
三、解答题:本大题共5小题,共40分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分6分)从点发出的一束直线光线射到轴上,经轴反射后与圆相切,求光线所在的直线方程。
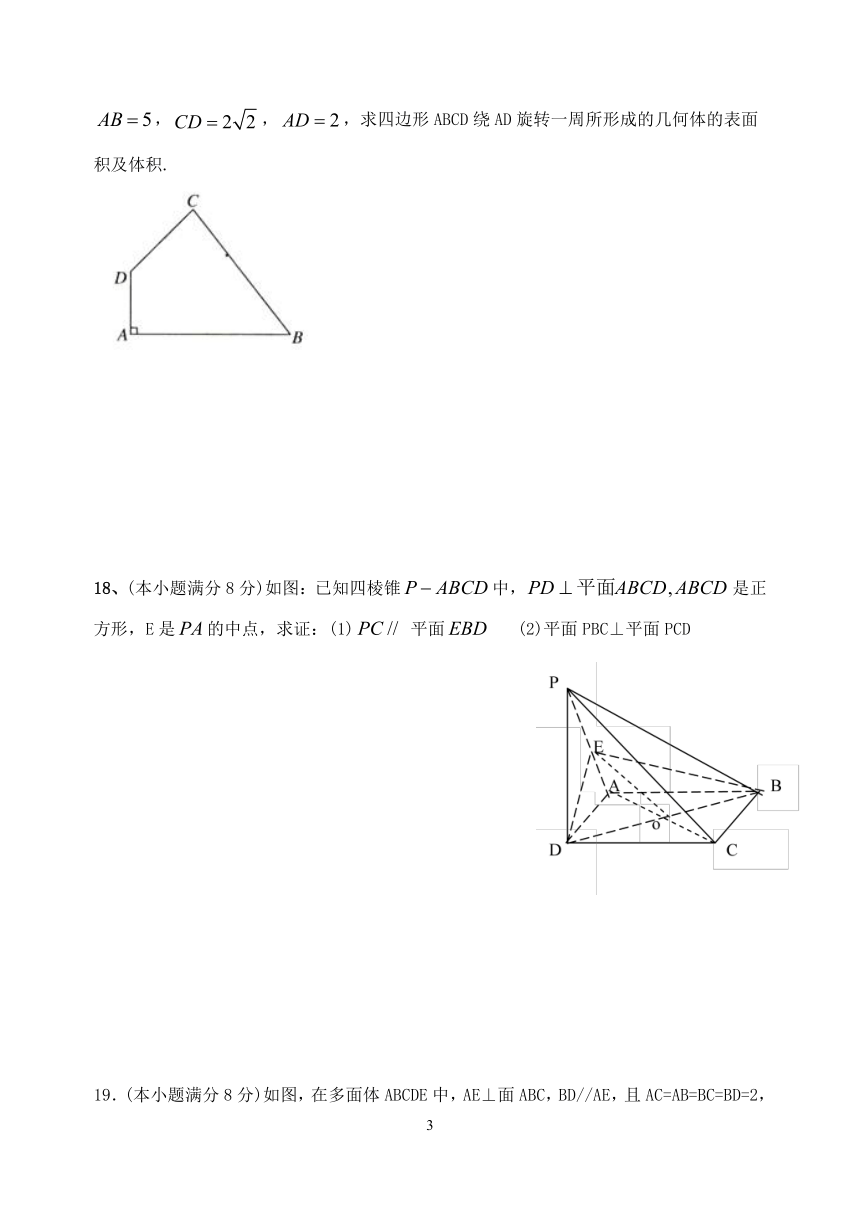
17.(本小题满分8分)如图所示,在四边形ABCD中,,,,,,求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.
18、(本小题满分8分)如图:已知四棱锥中,是正方形,E是的中点,求证:(1)
平面
(2)平面PBC⊥平面PCD
19.(本小题满分8分)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点。(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成二面角的余弦值。
20.(本小题满分10分)
已知圆C经过、两点,且圆心在直线上.
(1)求圆C的方程;
(2)若直线经过点且与圆C相切,求直线的方程.
数学模拟试题答案
一、选择题:(本大题共10小题,每小题4分,共40分)
DBCDA
CABAD
3、填空题:(本大题共5小题,每小题4分,共20分)
11.
12.x-4y+28=1
13.x+y+1=0
14.
15.②③
三、解答题:本大题共5小题,共40分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分6分)从点发出的一束直线光线射到轴上,经轴反射后与圆相切,求光线所在的直线方程。
16.(6分)解:圆的圆心坐标为(2,2),
半径为1;
点P
关于轴对称的点为Q(-3,-3),
设反身光线斜率为,显然存在,方程为
,也就是
由圆心(2,2)到直线的距离为半径1得:
,解得。
故入射光线的斜率为,方程为
.
17.(本小题满分8分)如图所示,在四边形ABCD中,,,,,,求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.
17..
18、(本小题满分8分)如图:已知四棱锥中,是正方形,E是的中点,求证:(1)
平面
(2)平面PBC⊥平面PCD
18、证:(1)连接AC交BD与O,连接EO,
∵E、O分别为PA、AC的中点
∴EO∥PC
∵PC平面EBD,EO平面EBD
∴PC∥平面EBD
(2)∵PD平面ABCD,
PD平面PCD,
∴平面PCD平面ABCD,
∵ABCD为正方形
∴
BCCD,
∵平面PCD∩平面ABCD=CD,
BC平面ABCD
∴BC平面PCD
又∵BC平面PBC,∴平面PBC平面PCD.
19.(本小题满分8分)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点。(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成二面角的余弦值。
19.(8分)(1)证明:取BC中点G,连FG,AG。
∵AE⊥面ABC,BD//AE,∴BD⊥面ABC,
又AG面ABC,∴BD⊥AG,
又AC=AB,G是BC中点,
∴AG⊥BC,∴AG⊥平面BCD。
∵F是CD中点且BD=2,
∴FG//BD且FG=BD=1,
∴FG//AE。……(2分)
又AE=1,∴AE=FG,故四边形AEFG是平行四边形,从而EF//AG。
∴EF⊥面BCD。……(4分)
(2)解:取AB中点H,则H为C在平面ABDE上的射影。过C作CK⊥DE于K,边接KH,由三垂线定理的逆定理得KH⊥DE,
∴∠HKC为二面角C—DE—B的平面角。……(6分)
易知,,,
由,可得。
在RtΔCHK中,,故。
∴面CDE与面ABDE所成的二面角的余弦值为。……(8分)
20.(本小题满分10分)
已知圆C经过、两点,且圆心在直线上.
(1)求圆C的方程;
(2)若直线经过点且与圆C相切,求直线的方程.
【解】(1)方法1:设圆的方程为,
依题意得:
……………3分
解得.
……………4分
所以圆的方程为.
……………5分
方法2:因为、,所以线段中点的坐标为,
直线的斜率,……………1分
因此直线的垂直平分线的方程是,即.………3分
圆心的坐标是方程组的解.
解此方程组,得即圆心的坐标为.
……………4分
圆心为的圆的半径长.
所以圆的方程为.
……………5分
(2)由于直线经过点,
当直线的斜率不存在时,与圆相离.
当直线的斜率存在时,可设直线的方程为,
即:.
……………7分
因为直线与圆相切,且圆的圆心为,半径为,所以有
.
……………8分
解得或.
……………9分
所以直线的方程为或,
即:或.……………10分
正视图
侧视图
俯视图
A
B
A1
B1
C
C1
正视图
侧视图
俯视图
E
D
C
B
A
P
PAGE
4
一、选择题:(本大题共10小题,每小题4分,共40分)
1.如图是一个几何体的三视图,则该几何体为(
)
A.球
B.圆柱
C.圆台
D.圆锥
2.下列命题正确的是(
)
A.如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
B.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
C.垂直于同一条直线的两条直线相互垂直
D.若两条直线与第三条直线所成的角相等,则这两条直线互相平行
3、如右图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为(
)
A、6+
B、24+
C、24+2
D、32
4.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是(
)
A.
B.
C.
D.
5.
已知直线:和圆C:
,则直线和圆C的位置关系为(
).
A.相交
B.
相切
C.相离
D.
不能确定
6、直线的倾斜角为(
)
A、300
B、600
C、1200
D、1500
7.直线与圆没有公共点,则的取值范围是(
)
A.
B.
C.
D.
8.已知直线与直线平行,则的值为
(
)
A.
B.
C.
D.
9、直线2x+y+5=0上的点到原点距离的最小值为
(
)
A.
B.
C.
D.
10.互相垂直,则的值是
A.
-3
B.
0
C.
0或-3
D.
0或1
2、填空题:(本大题共5小题,每小题4分,共20分)
11.直线的斜率是
,在轴的截距为
12.
已知直线过点(0,7),且与直线垂直,则直线的方程为
13.经过圆的圆心,且与直线平行的直线方程是
.
14.已知圆C:=4及直线l:x-y+3=0,则直线被C截得的弦长为
15.设有四个条件:①平面与平面、所成的锐二面角相等;②直线a//b,a⊥平面,b⊥平面;③a、b是异面直线,a,b,且a//,b//;④平面内距离为d的两条直线在平面内的射影仍为两条距离为d的平行线。
其中能推出//的条件有
。(填写所有正确条件的代号)
三、解答题:本大题共5小题,共40分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分6分)从点发出的一束直线光线射到轴上,经轴反射后与圆相切,求光线所在的直线方程。
17.(本小题满分8分)如图所示,在四边形ABCD中,,,,,,求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.
18、(本小题满分8分)如图:已知四棱锥中,是正方形,E是的中点,求证:(1)
平面
(2)平面PBC⊥平面PCD
19.(本小题满分8分)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点。(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成二面角的余弦值。
20.(本小题满分10分)
已知圆C经过、两点,且圆心在直线上.
(1)求圆C的方程;
(2)若直线经过点且与圆C相切,求直线的方程.
数学模拟试题答案
一、选择题:(本大题共10小题,每小题4分,共40分)
DBCDA
CABAD
3、填空题:(本大题共5小题,每小题4分,共20分)
11.
12.x-4y+28=1
13.x+y+1=0
14.
15.②③
三、解答题:本大题共5小题,共40分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分6分)从点发出的一束直线光线射到轴上,经轴反射后与圆相切,求光线所在的直线方程。
16.(6分)解:圆的圆心坐标为(2,2),
半径为1;
点P
关于轴对称的点为Q(-3,-3),
设反身光线斜率为,显然存在,方程为
,也就是
由圆心(2,2)到直线的距离为半径1得:
,解得。
故入射光线的斜率为,方程为
.
17.(本小题满分8分)如图所示,在四边形ABCD中,,,,,,求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.
17..
18、(本小题满分8分)如图:已知四棱锥中,是正方形,E是的中点,求证:(1)
平面
(2)平面PBC⊥平面PCD
18、证:(1)连接AC交BD与O,连接EO,
∵E、O分别为PA、AC的中点
∴EO∥PC
∵PC平面EBD,EO平面EBD
∴PC∥平面EBD
(2)∵PD平面ABCD,
PD平面PCD,
∴平面PCD平面ABCD,
∵ABCD为正方形
∴
BCCD,
∵平面PCD∩平面ABCD=CD,
BC平面ABCD
∴BC平面PCD
又∵BC平面PBC,∴平面PBC平面PCD.
19.(本小题满分8分)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点。(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成二面角的余弦值。
19.(8分)(1)证明:取BC中点G,连FG,AG。
∵AE⊥面ABC,BD//AE,∴BD⊥面ABC,
又AG面ABC,∴BD⊥AG,
又AC=AB,G是BC中点,
∴AG⊥BC,∴AG⊥平面BCD。
∵F是CD中点且BD=2,
∴FG//BD且FG=BD=1,
∴FG//AE。……(2分)
又AE=1,∴AE=FG,故四边形AEFG是平行四边形,从而EF//AG。
∴EF⊥面BCD。……(4分)
(2)解:取AB中点H,则H为C在平面ABDE上的射影。过C作CK⊥DE于K,边接KH,由三垂线定理的逆定理得KH⊥DE,
∴∠HKC为二面角C—DE—B的平面角。……(6分)
易知,,,
由,可得。
在RtΔCHK中,,故。
∴面CDE与面ABDE所成的二面角的余弦值为。……(8分)
20.(本小题满分10分)
已知圆C经过、两点,且圆心在直线上.
(1)求圆C的方程;
(2)若直线经过点且与圆C相切,求直线的方程.
【解】(1)方法1:设圆的方程为,
依题意得:
……………3分
解得.
……………4分
所以圆的方程为.
……………5分
方法2:因为、,所以线段中点的坐标为,
直线的斜率,……………1分
因此直线的垂直平分线的方程是,即.………3分
圆心的坐标是方程组的解.
解此方程组,得即圆心的坐标为.
……………4分
圆心为的圆的半径长.
所以圆的方程为.
……………5分
(2)由于直线经过点,
当直线的斜率不存在时,与圆相离.
当直线的斜率存在时,可设直线的方程为,
即:.
……………7分
因为直线与圆相切,且圆的圆心为,半径为,所以有
.
……………8分
解得或.
……………9分
所以直线的方程为或,
即:或.……………10分
正视图
侧视图
俯视图
A
B
A1
B1
C
C1
正视图
侧视图
俯视图
E
D
C
B
A
P
PAGE
4
同课章节目录
