5.2.2 平行线的判定课课练(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册﹒课课练
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
一、选择题
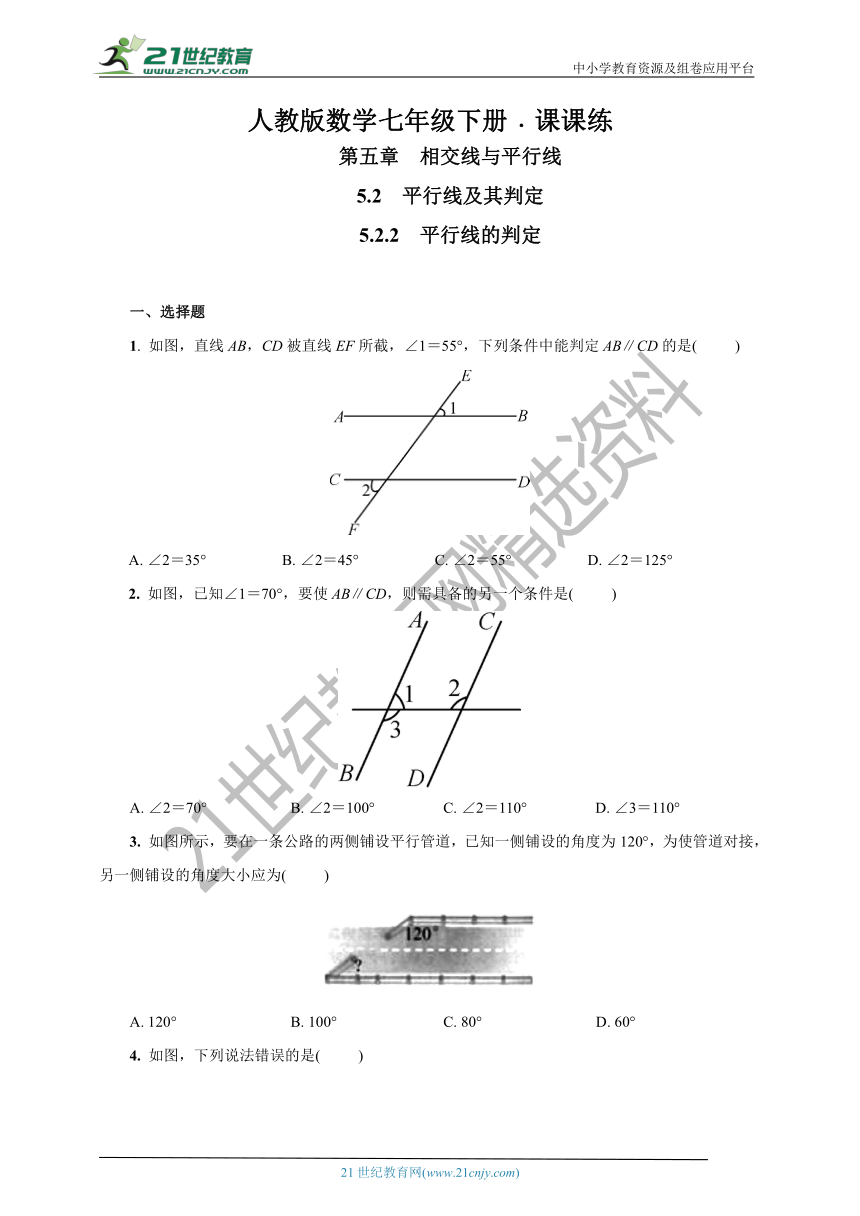
1.
如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是(
)
A.
∠2=35°
B.
∠2=45°
C.
∠2=55°
D.
∠2=125°
2.
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是(
)
A.
∠2=70°
B.
∠2=100°
C.
∠2=110°
D.
∠3=110°
3.
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为(
)
A.
120°
B.
100°
C.
80°
D.
60°
4.
如图,下列说法错误的是(
)
A.
若a∥b,b∥c,则a∥c
B.
若∠1=∠2,则a∥c
C.
若∠3=∠2,则b∥c
D.
若∠3+∠5=180°,则a∥c
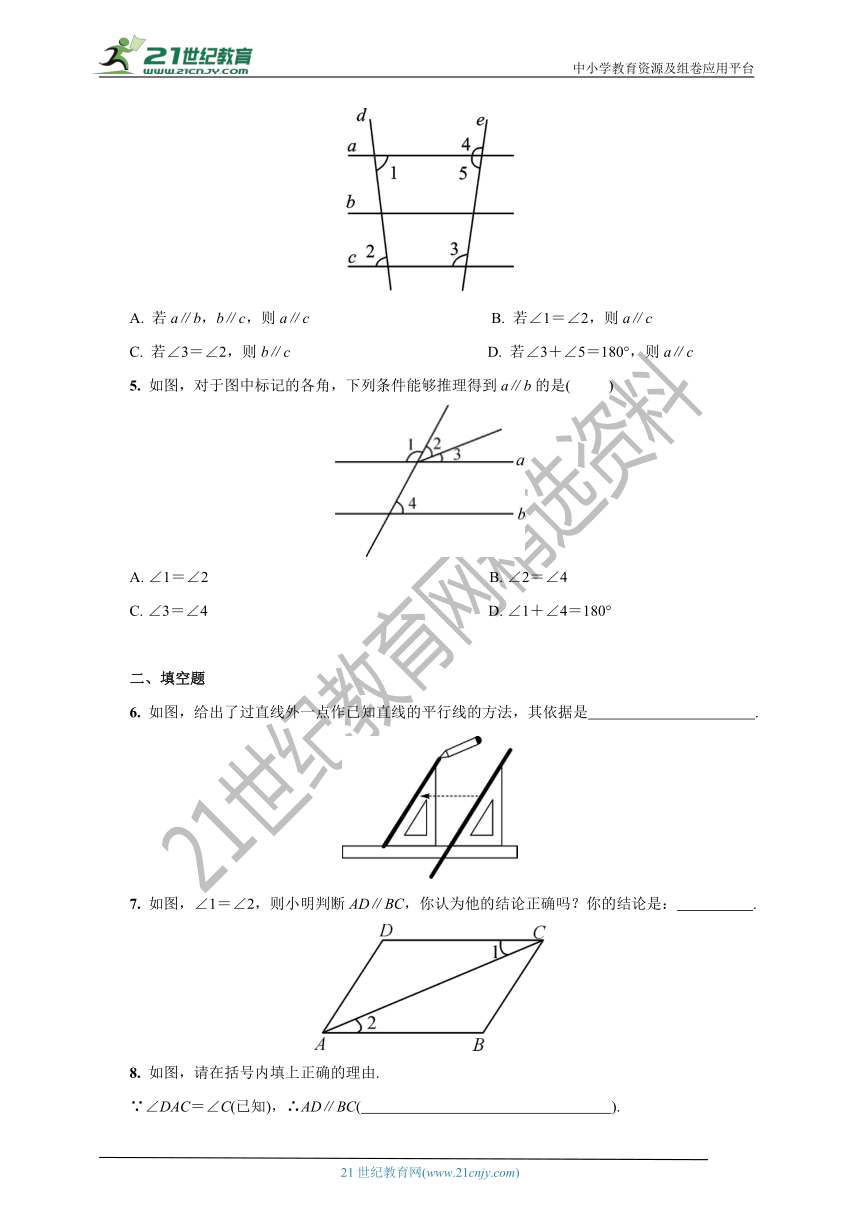
5.
如图,对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.
∠1=∠2
B.
∠2=∠4
C.
∠3=∠4
D.
∠1+∠4=180°
二、填空题
6.
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
.
7.
如图,∠1=∠2,则小明判断AD∥BC,你认为他的结论正确吗?你的结论是:
.
8.
如图,请在括号内填上正确的理由.
∵∠DAC=∠C(已知),∴AD∥BC(
).
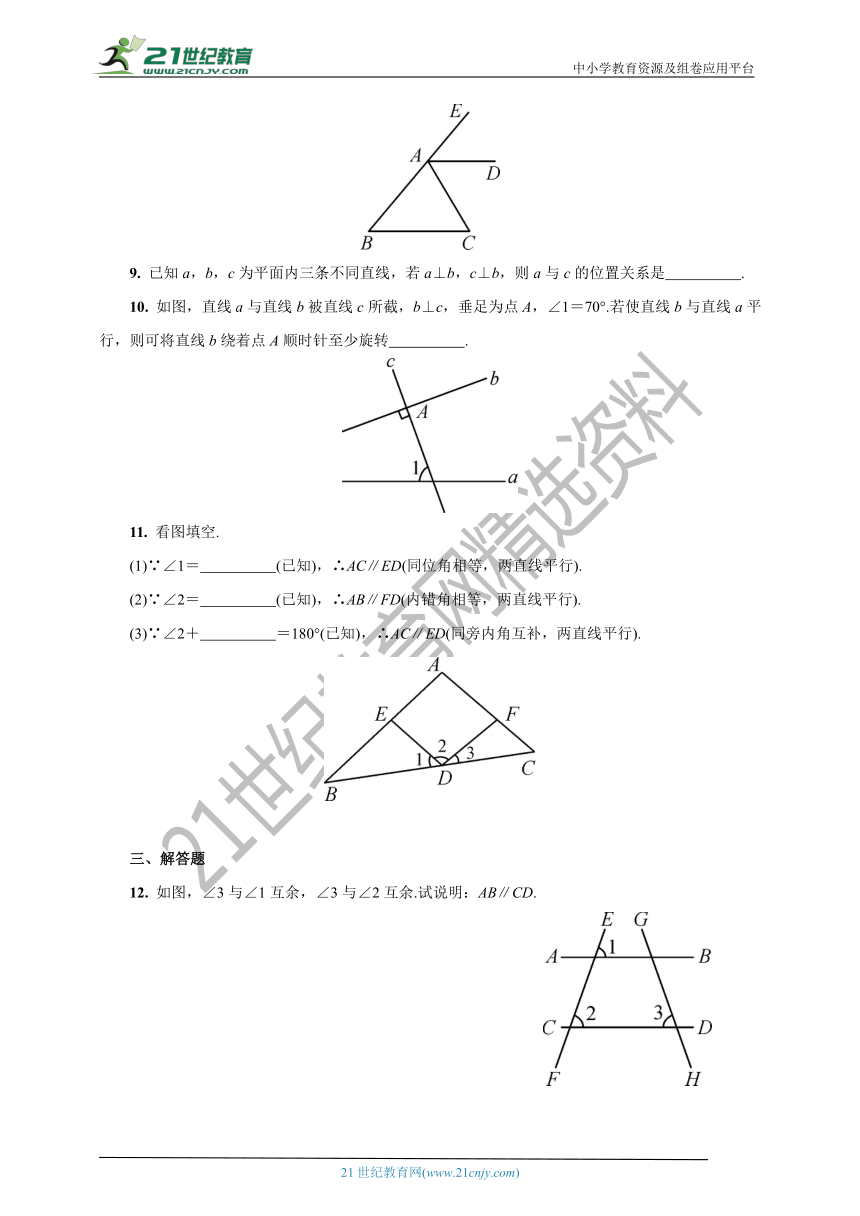
9.
已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是
.
10.
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转
.
11.
看图填空.
(1)∵∠1=
(已知),∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=
(已知),∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+
=180°(已知),∴AC∥ED(同旁内角互补,两直线平行).
三、解答题
12.
如图,∠3与∠1互余,∠3与∠2互余.试说明:AB∥CD.
13.
如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
14.
如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
15.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
16.
如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
17.
如图,∠BAF=46°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
18.
如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参
考
答
案
1.
C
2.
C
3.
D
4.
C
5.
D
6.
同位角相等,两直线平行
7.
AB∥CD
8.
内错角相等,两直线平行
9.
平行
10.
20°
11.
(1)∠C
(2)∠BED
(3)∠AFD
12.
解:∵∠3与∠1互余,∠3与∠2互余,∴∠1=∠2.
∴AB∥CD.
13.
解:∵∠ACD=70°,∠ACB=60°,∴∠BCD=130°.
∵∠ABC=50°,∴∠BCD+∠ABC=180°.
∴AB∥CD.
14.
解:∵∠A=∠C,∠B=∠D,∴∠B+∠C=∠D+∠A=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,
∠B=∠D,∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
15.
解:CF∥AB.
理由如下:∵图中是一副直角三角板,∴∠BAC=45°.
∵CF平分∠DCE,∠DCE=90°,∴∠DCF=∠DCE=45°.
∴∠DCF=∠BAC.
∴CF∥AB.
16.
解:PG∥QH,AB∥CD.
理由如下:∵PG平分∠APQ,QH平分∠DQP,∴∠1=∠GPQ=∠APQ,∠PQH=∠2=∠PQD.
又∵∠1=∠2,∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
17.
解:CD∥AB.
理由如下:∵CE⊥CD,∴∠DCE=90°.
∵∠ACE=136°,∴∠ACD=360°-136°-90°=134°.
∵∠BAF=46°,∴∠BAC=180°-∠BAF=180°-46°=134°.
∴∠ACD=∠BAC.
∴CD∥AB.
18.
解:CD∥EF.
理由如下:∵AB⊥BD,CD⊥BD,∴AB∥CD.
∵∠1+∠2=180°,∴AB∥EF.
∴CD∥EF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版数学七年级下册﹒课课练
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
一、选择题
1.
如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是(
)
A.
∠2=35°
B.
∠2=45°
C.
∠2=55°
D.
∠2=125°
2.
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是(
)
A.
∠2=70°
B.
∠2=100°
C.
∠2=110°
D.
∠3=110°
3.
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为(
)
A.
120°
B.
100°
C.
80°
D.
60°
4.
如图,下列说法错误的是(
)
A.
若a∥b,b∥c,则a∥c
B.
若∠1=∠2,则a∥c
C.
若∠3=∠2,则b∥c
D.
若∠3+∠5=180°,则a∥c
5.
如图,对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.
∠1=∠2
B.
∠2=∠4
C.
∠3=∠4
D.
∠1+∠4=180°
二、填空题
6.
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
.
7.
如图,∠1=∠2,则小明判断AD∥BC,你认为他的结论正确吗?你的结论是:
.
8.
如图,请在括号内填上正确的理由.
∵∠DAC=∠C(已知),∴AD∥BC(
).
9.
已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是
.
10.
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转
.
11.
看图填空.
(1)∵∠1=
(已知),∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=
(已知),∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+
=180°(已知),∴AC∥ED(同旁内角互补,两直线平行).
三、解答题
12.
如图,∠3与∠1互余,∠3与∠2互余.试说明:AB∥CD.
13.
如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
14.
如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
15.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
16.
如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
17.
如图,∠BAF=46°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
18.
如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参
考
答
案
1.
C
2.
C
3.
D
4.
C
5.
D
6.
同位角相等,两直线平行
7.
AB∥CD
8.
内错角相等,两直线平行
9.
平行
10.
20°
11.
(1)∠C
(2)∠BED
(3)∠AFD
12.
解:∵∠3与∠1互余,∠3与∠2互余,∴∠1=∠2.
∴AB∥CD.
13.
解:∵∠ACD=70°,∠ACB=60°,∴∠BCD=130°.
∵∠ABC=50°,∴∠BCD+∠ABC=180°.
∴AB∥CD.
14.
解:∵∠A=∠C,∠B=∠D,∴∠B+∠C=∠D+∠A=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,
∠B=∠D,∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
15.
解:CF∥AB.
理由如下:∵图中是一副直角三角板,∴∠BAC=45°.
∵CF平分∠DCE,∠DCE=90°,∴∠DCF=∠DCE=45°.
∴∠DCF=∠BAC.
∴CF∥AB.
16.
解:PG∥QH,AB∥CD.
理由如下:∵PG平分∠APQ,QH平分∠DQP,∴∠1=∠GPQ=∠APQ,∠PQH=∠2=∠PQD.
又∵∠1=∠2,∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
17.
解:CD∥AB.
理由如下:∵CE⊥CD,∴∠DCE=90°.
∵∠ACE=136°,∴∠ACD=360°-136°-90°=134°.
∵∠BAF=46°,∴∠BAC=180°-∠BAF=180°-46°=134°.
∴∠ACD=∠BAC.
∴CD∥AB.
18.
解:CD∥EF.
理由如下:∵AB⊥BD,CD⊥BD,∴AB∥CD.
∵∠1+∠2=180°,∴AB∥EF.
∴CD∥EF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
