沪科版八年级数学下册 第18章勾股定理测试卷(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 第18章勾股定理测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 00:00:00 | ||
图片预览



文档简介
第18章 勾股定理测试题
一、选择题(本大题共10小题,每小题4分,满分40分)
1.△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A.3个 B.2个 C.1个 D.4个
2.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A. 26?? ? ? B. 21 C. 20? ?? ?????? D. 18??
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
?A.25?? ???? B.14??? ???? C.7????? ???? D.7或25
4.若△ABC的三边a.b.c,满足(a-b)(a2+b2-c2)=0,则△ABC是(? )
A.等腰三角形? B.直角三角形 C.等腰三角形或直角三角形? D.等腰直角三角形
如图,将三边长分别为3,4,5的△ABC沿最长边翻转180°成△ABC1,则CC1的长等于( )
A. B. C. D.
第5题图 第6题图
6.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上答案都不对
7. 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,则MN=( )
A. B. C. D.
8.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为10 cm,正方形A的边长为6 cm、B的边长为5 cm、C的边长为5 cm,则正方形D的边长为( )
A. ? ? B.4 cm ? ? C. D.3 cm
9.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )
A.2cm? B.3cm? C.4cm? D.5cm
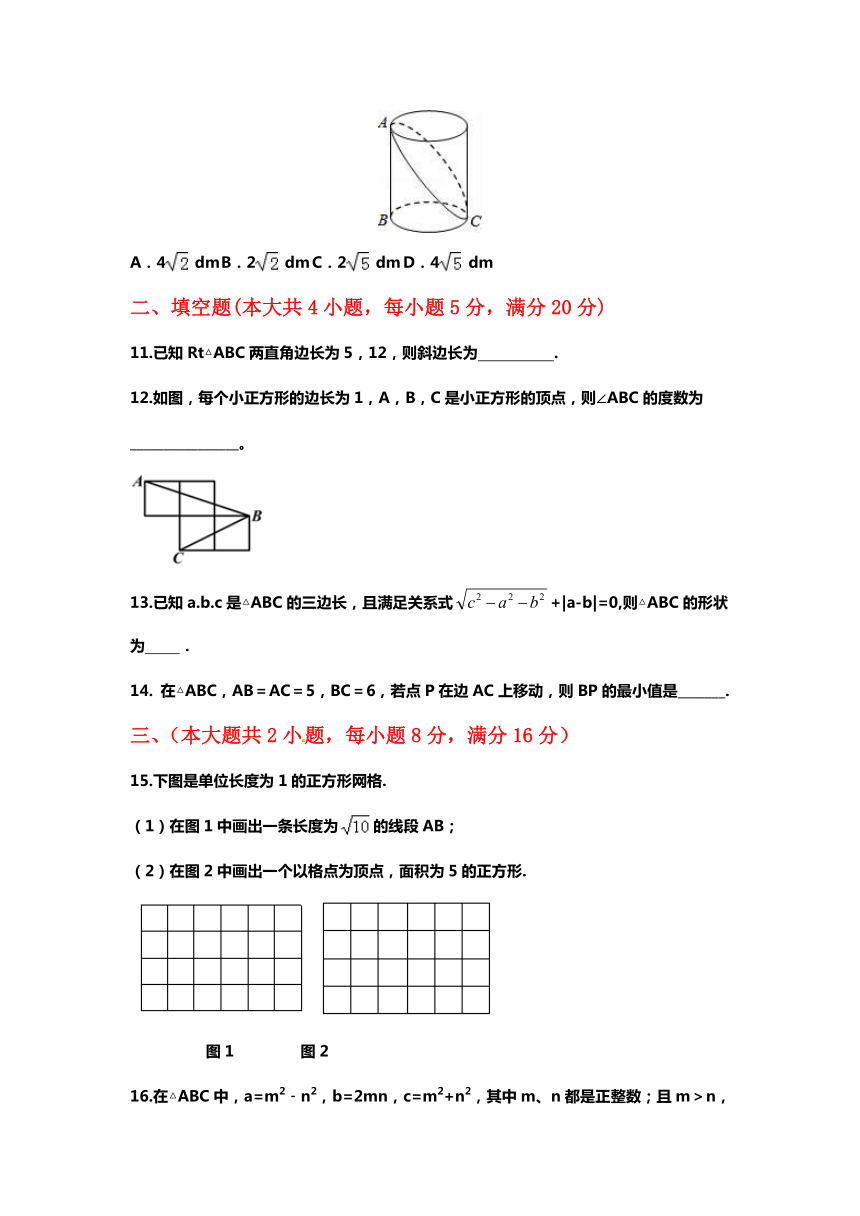
10.如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A.4 dm B.2 dm C.2 dm D.4 dm
二、填空题(本大共4小题,每小题5分,满分20分)
11.已知Rt△ABC两直角边长为5,12,则斜边长为 .
12.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为________________。
13.已知a.b.c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为?????? .?
14. 在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
三、(本大题共2小题,每小题8分,满分16分)
15.下图是单位长度为1的正方形网格.
(1)在图1中画出一条长度为的线段AB;
(2)在图2中画出一个以格点为顶点,面积为5的正方形.
?
图1??? ?? ??? 图2?????????
16.在△ABC中,a=m2﹣n2,b=2mn,c=m2+n2,其中m、n都是正整数;且m>n,试判断△ABC是否为直角三角形?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,有一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积。
??
18. 阅读下列解题过程:已知、、为△ABC的三边,且满足,
试判断△ABC的形状.
解:∵ ①
∴ ②
∴ ③
∴ △ABC为直角三角形.
问:⑴上述解题过程,从哪一步开始出现错误?请写出该步的代号 ;
(2)错误的原因是 ;
(3)本题的正确结论是 .
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,正方形中,边上有一点,在上有一点,使为最短,求的最短距离.
20..在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
六、(本题满分12分)
21. 在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边. 另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高的高度.
七、(本题满分12分)
22.如图,△ABC,△AED是两个大小一样的三角形,已知∠ADE=90°,AE=5,AD=4,连接EB,求DE和EB的长.
八、(本题满分14分)
23.长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.
(1)求BC长;
(2)求阴影部分的面积.
参考答案
A 2.C 3.D 4.C 5.D 6.B 7.A 8.C 9.B 10.B
13 12.450 13.等腰直角三角形 14. 24/5
15.(图略).
16.解:∵a=m2-n2,b=2mn,c=m2+n2,∴a2+b2=(m2-n2)2+4m2n2=m4+n4-2m2n2+4m2n2=m4+n4+2m2n2=(m2+n2)2=c2.∴△ABC是为直角三角形.
17.解:连接AC,∵∠ADC=90°,AD=4,CD=3,∴AC2=AD2+CD2=42+32=25,∴AC=5.又∵BC=12,AB=13,∴AC2+BC2=52+122=169,又∵AB2=169,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴S四边形ABCD=S△ABC-S△ADC=×12×5-×3×4=24m2.
18. ③; 没有考虑 的情况; △ABC为直角三角形或等腰三角形.
19.由正方形的对角线互相垂直平分,可得无论P在什么位置,都有PD=PB,故均有EP+BP=PE+PD成立.连接DE与AC,所得的交点,即为EP+BP的最小值时的位置,此时EP+BP=DE==5.即 的最短距离为5.
20.解:公路AB需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.因为BC=400米,AC=300米,∠ACB=90°,所以根据勾股定理有AB=500米.因为S△ABC=AB?CD=BC?AC,所以CD=240米.由于240米<250米,故有危险,因此AB段公路需要暂时封锁.
21. 解:设树高为xm,则BD=x-10,则题意可知CD+AC=10+20=30,∴AB=30-BD=30-(x-10)=40-x.∵△ABC为直角三角形,∴AB2=AC2+BC2,即(40-x)2=202+x2,解得x=15,即树高为15m.
22.解:∵∠ADE=90°,AE=5,AD=4,∴DE==3.∵△ABC,△AED是两个大小一样的三角形,∴AB=AE=5,∴BD=1,∴BE=
23.解:(1)∵长方形OABC绕顶点C(0,5)逆时针方向旋转得到矩形CO′A′B′,∴BC=AO=
O′A′,AB=CO=CO'=5,∠B=∠O'=90°.∵AD=4,AB=5,∴BD=5-4=1.设BC=x,则DO'=O'A'-A'D=x-2.连接CD,则BC2+BD2=CD2=CO'2+DO'2,即x2+12=52+(x-2)2
解得x=7,∴BC=7.
(2)∵BC=7,BD=1,CO'=5,DO'=7-2=5,∠B=∠O'=90°,∴阴影部分的面积=△BCD面积+△O'CD面积=
D
A
B
C
E
D
B
C
A
一、选择题(本大题共10小题,每小题4分,满分40分)
1.△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A.3个 B.2个 C.1个 D.4个
2.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A. 26?? ? ? B. 21 C. 20? ?? ?????? D. 18??
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
?A.25?? ???? B.14??? ???? C.7????? ???? D.7或25
4.若△ABC的三边a.b.c,满足(a-b)(a2+b2-c2)=0,则△ABC是(? )
A.等腰三角形? B.直角三角形 C.等腰三角形或直角三角形? D.等腰直角三角形
如图,将三边长分别为3,4,5的△ABC沿最长边翻转180°成△ABC1,则CC1的长等于( )
A. B. C. D.
第5题图 第6题图
6.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上答案都不对
7. 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,则MN=( )
A. B. C. D.
8.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为10 cm,正方形A的边长为6 cm、B的边长为5 cm、C的边长为5 cm,则正方形D的边长为( )
A. ? ? B.4 cm ? ? C. D.3 cm
9.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )
A.2cm? B.3cm? C.4cm? D.5cm
10.如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A.4 dm B.2 dm C.2 dm D.4 dm
二、填空题(本大共4小题,每小题5分,满分20分)
11.已知Rt△ABC两直角边长为5,12,则斜边长为 .
12.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为________________。
13.已知a.b.c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为?????? .?
14. 在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
三、(本大题共2小题,每小题8分,满分16分)
15.下图是单位长度为1的正方形网格.
(1)在图1中画出一条长度为的线段AB;
(2)在图2中画出一个以格点为顶点,面积为5的正方形.
?
图1??? ?? ??? 图2?????????
16.在△ABC中,a=m2﹣n2,b=2mn,c=m2+n2,其中m、n都是正整数;且m>n,试判断△ABC是否为直角三角形?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,有一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积。
??
18. 阅读下列解题过程:已知、、为△ABC的三边,且满足,
试判断△ABC的形状.
解:∵ ①
∴ ②
∴ ③
∴ △ABC为直角三角形.
问:⑴上述解题过程,从哪一步开始出现错误?请写出该步的代号 ;
(2)错误的原因是 ;
(3)本题的正确结论是 .
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,正方形中,边上有一点,在上有一点,使为最短,求的最短距离.
20..在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
六、(本题满分12分)
21. 在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边. 另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高的高度.
七、(本题满分12分)
22.如图,△ABC,△AED是两个大小一样的三角形,已知∠ADE=90°,AE=5,AD=4,连接EB,求DE和EB的长.
八、(本题满分14分)
23.长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.
(1)求BC长;
(2)求阴影部分的面积.
参考答案
A 2.C 3.D 4.C 5.D 6.B 7.A 8.C 9.B 10.B
13 12.450 13.等腰直角三角形 14. 24/5
15.(图略).
16.解:∵a=m2-n2,b=2mn,c=m2+n2,∴a2+b2=(m2-n2)2+4m2n2=m4+n4-2m2n2+4m2n2=m4+n4+2m2n2=(m2+n2)2=c2.∴△ABC是为直角三角形.
17.解:连接AC,∵∠ADC=90°,AD=4,CD=3,∴AC2=AD2+CD2=42+32=25,∴AC=5.又∵BC=12,AB=13,∴AC2+BC2=52+122=169,又∵AB2=169,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴S四边形ABCD=S△ABC-S△ADC=×12×5-×3×4=24m2.
18. ③; 没有考虑 的情况; △ABC为直角三角形或等腰三角形.
19.由正方形的对角线互相垂直平分,可得无论P在什么位置,都有PD=PB,故均有EP+BP=PE+PD成立.连接DE与AC,所得的交点,即为EP+BP的最小值时的位置,此时EP+BP=DE==5.即 的最短距离为5.
20.解:公路AB需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.因为BC=400米,AC=300米,∠ACB=90°,所以根据勾股定理有AB=500米.因为S△ABC=AB?CD=BC?AC,所以CD=240米.由于240米<250米,故有危险,因此AB段公路需要暂时封锁.
21. 解:设树高为xm,则BD=x-10,则题意可知CD+AC=10+20=30,∴AB=30-BD=30-(x-10)=40-x.∵△ABC为直角三角形,∴AB2=AC2+BC2,即(40-x)2=202+x2,解得x=15,即树高为15m.
22.解:∵∠ADE=90°,AE=5,AD=4,∴DE==3.∵△ABC,△AED是两个大小一样的三角形,∴AB=AE=5,∴BD=1,∴BE=
23.解:(1)∵长方形OABC绕顶点C(0,5)逆时针方向旋转得到矩形CO′A′B′,∴BC=AO=
O′A′,AB=CO=CO'=5,∠B=∠O'=90°.∵AD=4,AB=5,∴BD=5-4=1.设BC=x,则DO'=O'A'-A'D=x-2.连接CD,则BC2+BD2=CD2=CO'2+DO'2,即x2+12=52+(x-2)2
解得x=7,∴BC=7.
(2)∵BC=7,BD=1,CO'=5,DO'=7-2=5,∠B=∠O'=90°,∴阴影部分的面积=△BCD面积+△O'CD面积=
D
A
B
C
E
D
B
C
A
