5.3.1 平行线的性质课课练(含答案)
图片预览

文档简介
人教版数学七年级下册﹒课课练
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
一、选择题
1. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
A. 45° B. 60° C. 90° D. 120°
2. 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A. 108° B. 82° C. 72° D. 62°
3. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A. 20° B. 35° C. 45° D. 70°
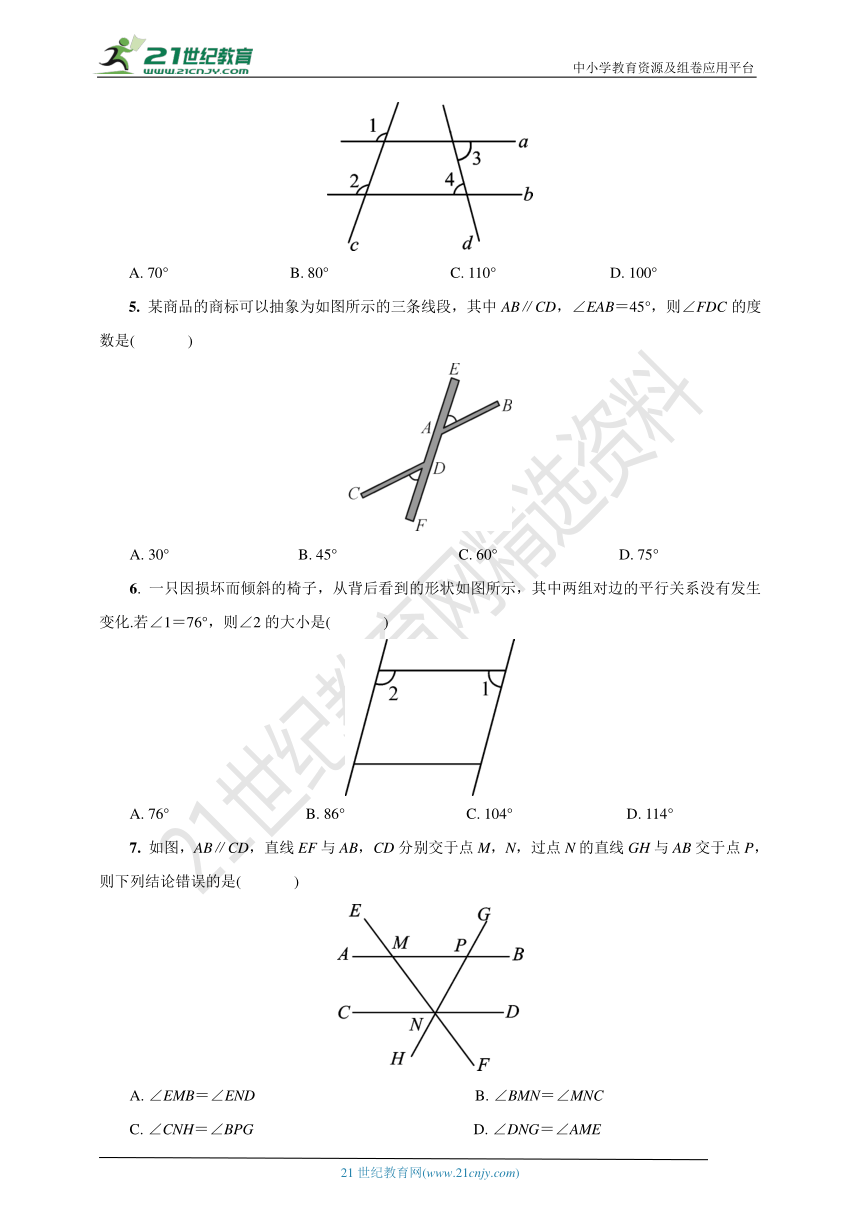
4. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=70°,则∠4的度数是( )
A. 70° B. 80° C. 110° D. 100°
5. 某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( )
A. 30° B. 45° C. 60° D. 75°
6. 一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化.若∠1=76°,则∠2的大小是( )
A. 76° B. 86° C. 104° D. 114°
7. 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END B. ∠BMN=∠MNC
C. ∠CNH=∠BPG D. ∠DNG=∠AME
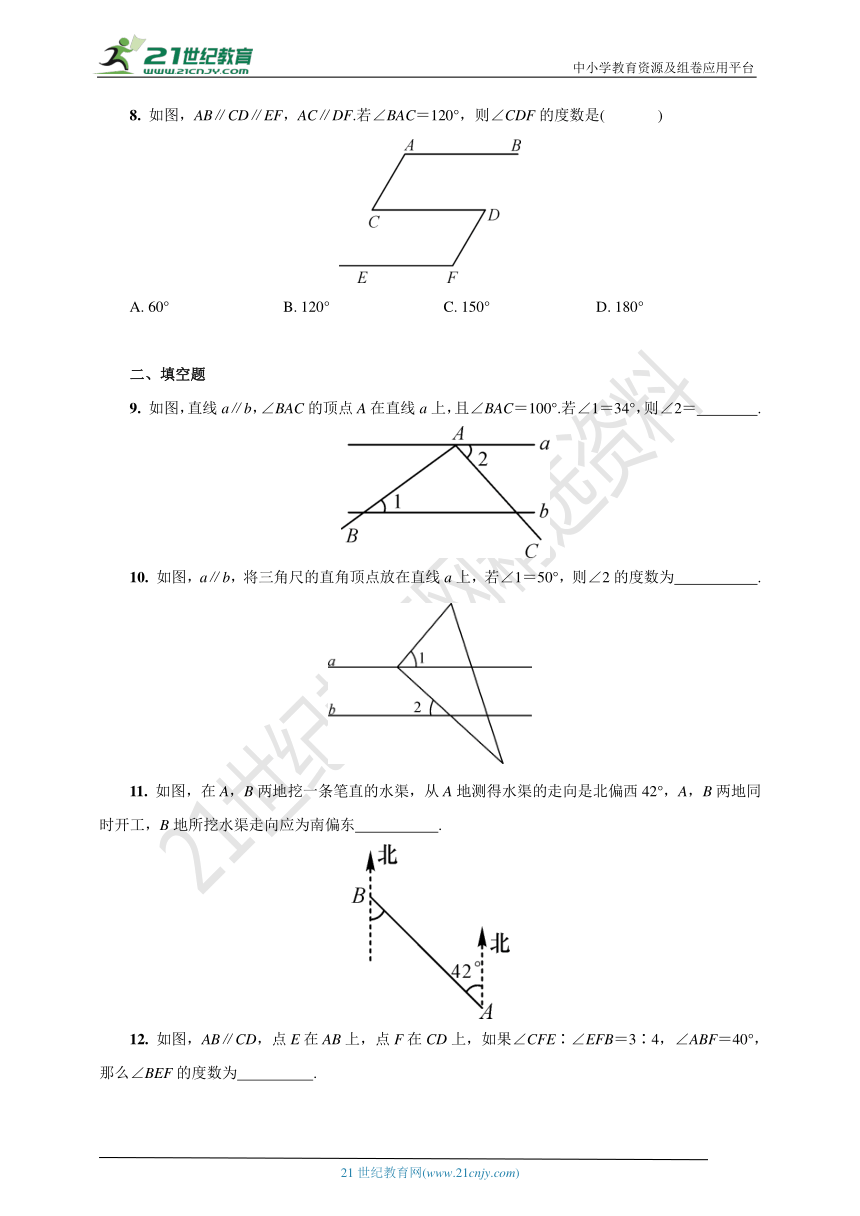
8. 如图,AB∥CD∥EF,AC∥DF.若∠BAC=120°,则∠CDF的度数是( )
A. 60° B. 120° C. 150° D. 180°
二、填空题
9. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= .
10. 如图,a∥b,将三角尺的直角顶点放在直线a上,若∠1=50°,则∠2的度数为 .
11. 如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东 .
12. 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
13. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′= .
三、解答题
14. 如图是某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
15. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
16. 如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
17. 阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
甲 乙 丙
参 考 答 案
1. C 2. C 3. B 4. A 5. B 6. C 7. D 8. A
9. 46°
10. 40°
11. 42°
12. 60°
13. 50°
14. 解:∵AD∥BC,∠A=115°,∠D=100°,∴∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-100°=80°.
15. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°. ∵EF平分∠AED,∴∠DEF=∠AED=69°. 又∵AB∥CD,∴∠AFE=∠DEF=69°.
16. 解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°. ∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°.∴∠DCF=50°. ∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
17. 解:如图乙,过点P作PE∥AB. ∵AB∥CD(已知),∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行). ∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等). ∵∠APC=∠EPA+∠EPC,∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB. ∴∠FPA=∠A(两直线平行,内错角相等). ∵AB∥CD(已知),∴PF∥CD(平行于同一条直线的两条直线互相平行). ∴∠FPC=∠C(两直线平行,内错角相等). ∵∠FPC-∠FPA=∠APC,∴∠C-∠A=∠APC(等量代换).
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
一、选择题
1. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
A. 45° B. 60° C. 90° D. 120°
2. 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A. 108° B. 82° C. 72° D. 62°
3. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A. 20° B. 35° C. 45° D. 70°
4. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=70°,则∠4的度数是( )
A. 70° B. 80° C. 110° D. 100°
5. 某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( )
A. 30° B. 45° C. 60° D. 75°
6. 一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化.若∠1=76°,则∠2的大小是( )
A. 76° B. 86° C. 104° D. 114°
7. 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END B. ∠BMN=∠MNC
C. ∠CNH=∠BPG D. ∠DNG=∠AME
8. 如图,AB∥CD∥EF,AC∥DF.若∠BAC=120°,则∠CDF的度数是( )
A. 60° B. 120° C. 150° D. 180°
二、填空题
9. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= .
10. 如图,a∥b,将三角尺的直角顶点放在直线a上,若∠1=50°,则∠2的度数为 .
11. 如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东 .
12. 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
13. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′= .
三、解答题
14. 如图是某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
15. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
16. 如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
17. 阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
甲 乙 丙
参 考 答 案
1. C 2. C 3. B 4. A 5. B 6. C 7. D 8. A
9. 46°
10. 40°
11. 42°
12. 60°
13. 50°
14. 解:∵AD∥BC,∠A=115°,∠D=100°,∴∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-100°=80°.
15. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°. ∵EF平分∠AED,∴∠DEF=∠AED=69°. 又∵AB∥CD,∴∠AFE=∠DEF=69°.
16. 解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°. ∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°.∴∠DCF=50°. ∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
17. 解:如图乙,过点P作PE∥AB. ∵AB∥CD(已知),∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行). ∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等). ∵∠APC=∠EPA+∠EPC,∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB. ∴∠FPA=∠A(两直线平行,内错角相等). ∵AB∥CD(已知),∴PF∥CD(平行于同一条直线的两条直线互相平行). ∴∠FPC=∠C(两直线平行,内错角相等). ∵∠FPC-∠FPA=∠APC,∴∠C-∠A=∠APC(等量代换).
