湘教版七年级数学下册 第4章 相交线与平行线 单元综合卷(含简单答案)
文档属性
| 名称 | 湘教版七年级数学下册 第4章 相交线与平行线 单元综合卷(含简单答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 00:00:00 | ||
图片预览


文档简介
第4章质量评估试卷
[时间:90分钟 分值:120分]
一、选择题(每小题3分,共30分)
1.下列各组图形,可以经过平移变换由一个图形得到另一个图形的是( )
2.如图1,AB∥CD,AD=CD,∠1=50°,则∠2的度数是 ( )
图1
A.55° B.60°
C.65° D.70°
3.如图2,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
图2
A.19° B.38°
C.42° D.52°
4.如图3,点P为直线l外一点,A,B,C,D为直线l上四点,PA=6 cm,PB=3 cm,PC=8 cm,PD⊥直线l,则点P到直线l的距离为( )
图3
A.3 cm B.小于3 cm
C.不小于3 cm D.大于6 cm
5.如图4,在△ABC中,BC=5,∠A=80°,把△ABC沿BC的方向平移到△DEF的位置,若CF=4,则下列结论中不一定正确的是( )
图4
A.BE=4 B.∠D=80°
C.AB∥DE D.DF=5
6.如图5,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件为( )
图5
A.①② B.①③
C.①④ D.③④
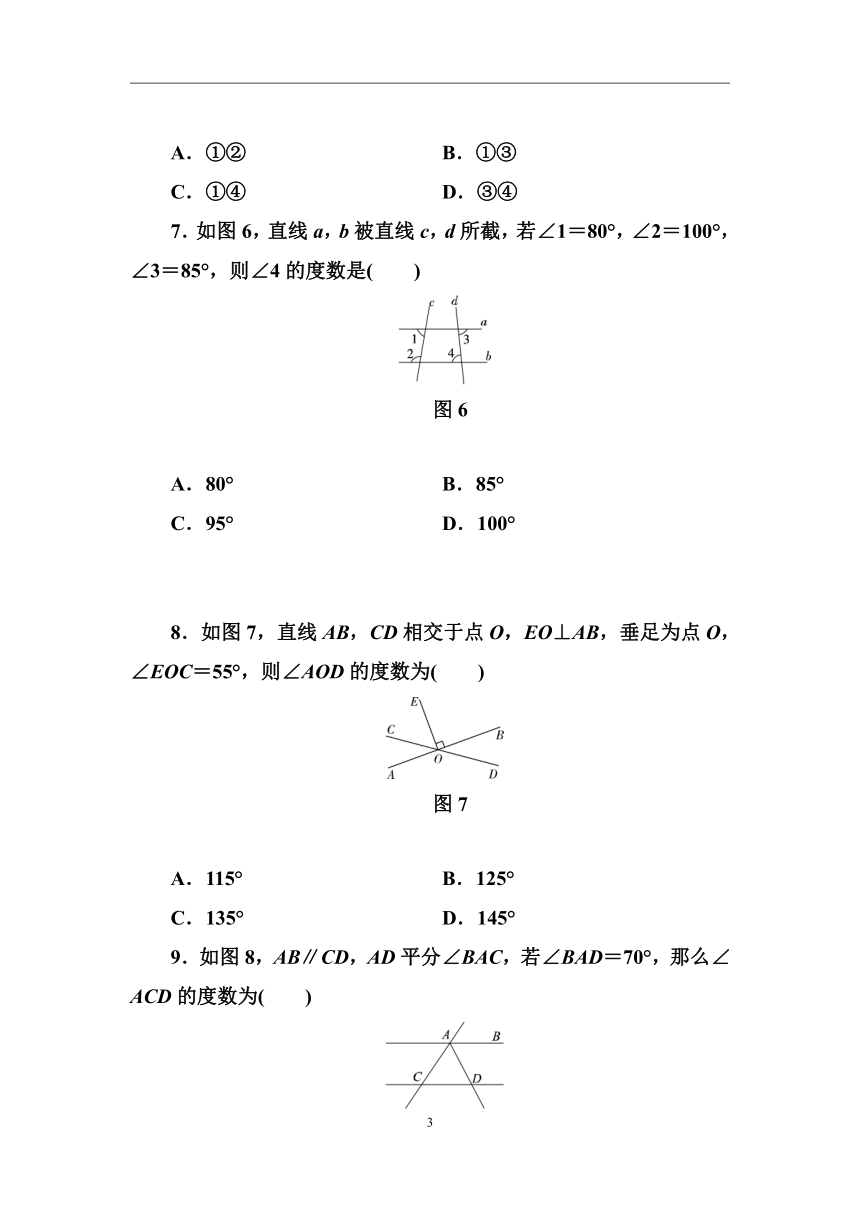
7.如图6,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
图6
A.80° B.85°
C.95° D.100°
8.如图7,直线AB,CD相交于点O,EO⊥AB,垂足为点O,∠EOC=55°,则∠AOD的度数为( )
图7
A.115° B.125°
C.135° D.145°
9.如图8,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )
图8
A.40° B.35°
C.50° D.45°
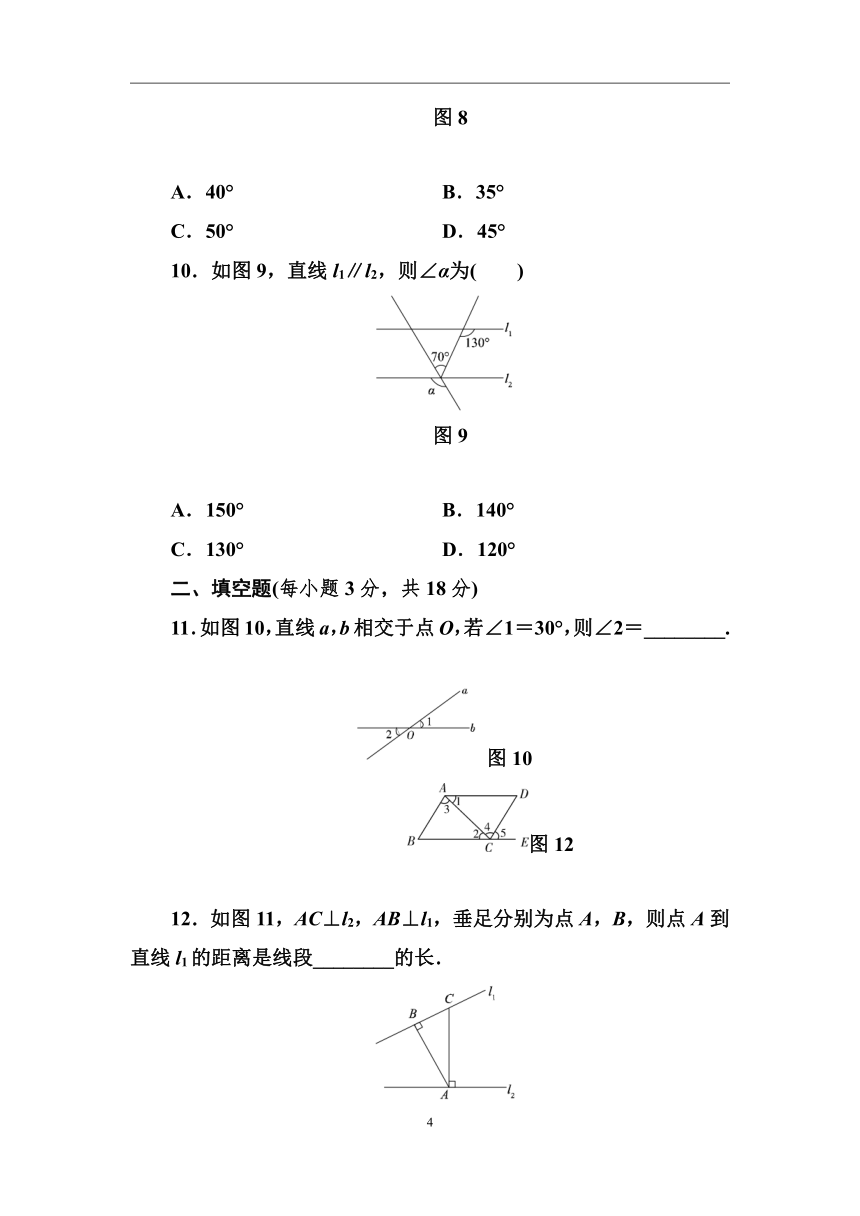
10.如图9,直线l1∥l2,则∠α为( )
图9
A.150° B.140°
C.130° D.120°
二、填空题(每小题3分,共18分)
11.如图10,直线a,b相交于点O,若∠1=30°,则∠2=________.
图10
图12
12.如图11,AC⊥l2,AB⊥l1,垂足分别为点A,B,则点A到直线l1的距离是线段________的长.
图11
13.如图12,要使AB∥CD,可以添加一个条件是_________________.
14.如图13,直线AB,CD交于点O,则∠BOD=________.
图13
15.如图14,△ABC中,AB=AC,BC=12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm 得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为________cm.
图14
16.如图15,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2的度数是________.
图15
三、解答题(共72分)
17.(8分)如图16,AB∥DC,AD∥BC,∠A=60°.求∠C的度数.
图16
18.(8分)如图17,AB∥CD,CE平分∠ACD,若∠1=25°,求∠2的度数.
图17
19.(10分)如图18,已知AC∥FG,∠1=∠2,判断DE与FG的位置关系,并说明理由.
图18
20.(11分)如图19,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
(1)求证:FD∥AB;
(2)求∠ACB的度数.
图19
21.(11分)如图20,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,∠AOE=26°,求∠COF的度数.
图20
22.(12分)如图21,∠A=106°,∠ABC=74°,BD⊥CD于点D,EF⊥CD于点F.求证:∠1=∠2.
图21
23.(12分)如图22,已知AB∥CD.
(1)试求图①中,∠A+∠C的度数;
(2)试求图②中,∠A+∠APC+∠C的度数;
(3)试求图③中,∠A+∠AEF+∠EFC+∠C的度数;
(4)如图④,按上述规律,∠A+…+∠C(共有n个角相加)的和为多少?
图22
参考答案
第4章质量评估试卷
1.A 2.C 3.D 4.B 5.D 6.A 7.B
8.D 9.A 10.D
11.30° 12.AB
13.∠3=∠4或∠B=∠5(答案不唯一)
14.60° 15.13 16.54° 17.60° 18.155°
19.DE∥FG,理由略.
20.(1)略 (2)50° 21.148° 22.略
23.(1)180° (2)360° (3)540° (4)(n-1)×180°
9
