人教版八年级数学下册17.2勾股定理的逆定理课时练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册17.2勾股定理的逆定理课时练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 00:00:00 | ||
图片预览


文档简介
(人教版)八年级下 第十七章 17.2 勾股定理的逆定理 课时练
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人 得分 一、选择题
1. 在△ABC中,∠A,∠B,∠C的对边分别为a,b,c且(a+b)(a-b)=c2,则( )
A. ∠A为直角?????????????B. ∠C为直角?????????????
?C. ∠B为直角?????????????D. △ABC不是直角三角形?????????????
2. 满足下列条件的三角形中,不是直角三角形的是 ( )
A. 三内角之比为1∶2∶3?????????????B. 三边长的平方之比为1∶2∶3?????????????
?C. 三边长之比为3∶4∶5?????????????D. 三内角之比为3∶4∶5?????????????
3. 下列几组数:①9,12,15,②8,15,17,③7,24,25,④n2-1,2n,n2+1(n是大于1的整数),其中是勾股数的有 ( )
A. 1组?????????????B. 2组?????????????C. 3组?????????????D. 4组?????????????
4. 以下定理,其中有逆定理的是( )
A. 对顶角相等?????????????
?B. 互为邻补角的角平分线互相垂直?????????????
?C. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补?????????????
?D. 直角三角形的两条直角边的平方和等于斜边的平方?????????????
5. 下列各组数中,是勾股数的是( )
A. 14,36,39?????????????B. 8,24,25?????????????C. 8,15,17?????????????D. 10,20,26?????????????
6. 如图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ABC的度数为?( )
?
A. 90°?????????????B. 60°?????????????C. 45°?????????????D. 30°?????????????
7. 一个三角形三边长a,b,c满足|a-12|++(c-20)2=0,则这个三角形最长边上的高为( )
A. 9.8?????????????B. 4.8?????????????C. 9.6?????????????D. 10?????????????
评卷人 得分 二、填空题
8. 如图所示,点A为小红家的位置,点B为小明家的位置,点C为学校的位置,三地之间的距离如图,已知学校在小明家的正西方向,则小红家在小明家的 方向.
?
9. 若一个三角形的三边长分别为m+1,m+2,m+3,那么当m= 时,这个三角形是直角三角形.?
10. 把命题“如果a>b,那么ac>bc(c≠0)”的逆命题改写为“如果……,那么……”的形式: ?
11. 已知a,b,c是△ABC的三边,且满足|a-3|++(c-5)2=0,则此三角形的形状是 .
评卷人 得分 三、解答题
12. 在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
13. 如图所示,已知△ABC的三边分别是a,b,c,且a+b=4,ab=1,c=,试判断△ABC的形状.
?
14. 如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
?
15. 如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
?
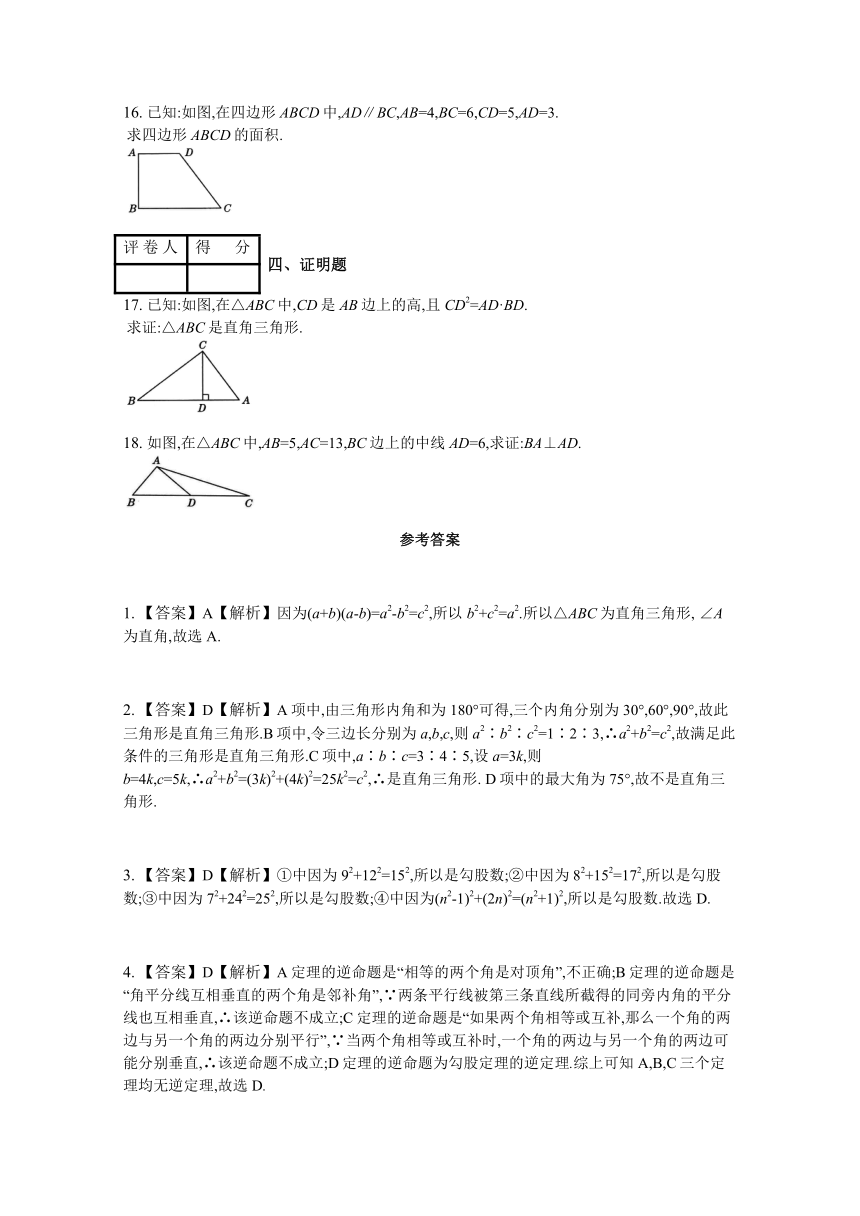
16. 已知:如图,在四边形ABCD中,AD∥BC,AB=4,BC=6,CD=5,AD=3.
?求四边形ABCD的面积.
?
评卷人 得分 四、证明题
17. 已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
?求证:△ABC是直角三角形.
?
18. 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,求证:BA⊥AD.
?
参考答案
1. 【答案】A【解析】因为(a+b)(a-b)=a2-b2=c2,所以b2+c2=a2.所以△ABC为直角三角形,?∠A为直角,故选A.
2. 【答案】D【解析】A项中,由三角形内角和为180°可得,三个内角分别为30°,60°,90°,故此三角形是直角三角形.B项中,令三边长分别为?a,b,c,则a2∶b2∶c2=1∶2∶3,∴a2+b2=c2,故满足此条件的三角形是直角三角形.C项中,a∶b∶c=3∶4∶5,设a=3k,则b=4k,c=5k,∴a2+b2=(3k)2+(4k)2=25k2=c2,∴是直角三角形.?D项中的最大角为75°,故不是直角三角形.
3. 【答案】D【解析】①中因为92+122=152,所以是勾股数;②中因为82+152=172,所以是勾股数;③中因为72+242=252,所以是勾股数;④中因为(n2-1)2+(2n)2=(n2+1)2,所以是勾股数.故选D.
4. 【答案】D【解析】A定理的逆命题是“相等的两个角是对顶角”,不正确;B定理的逆命题是“角平分线互相垂直的两个角是邻补角”,∵两条平行线被第三条直线所截得的同旁内角的平分线也互相垂直,∴该逆命题不成立;C定理的逆命题是“如果两个角相等或互补,那么一个角的两边与另一个角的两边分别平行”,∵当两个角相等或互补时,一个角的两边与另一个角的两边可能分别垂直,∴该逆命题不成立;D定理的逆命题为勾股定理的逆定理.综上可知A,B,C三个定理均无逆定理,故选D.
5. 【答案】C【解析】确定勾股数只需验证两小数的平方和与大数平方是否相等.
?∵142+362=1?492,392=1?521≠1?492,∴A项不是勾股数;
?∵82+242=640,252=625≠640,∴B项不是勾股数;
?∵82+152=289,172=289,∴C是勾股数;
?∵102+202=500,262=676≠500,∴D项不是勾股数.故选C.
6. 【答案】C【解析】连接AC,观察图形易知AB=,?BC=,?AC=,所以△ACB为等腰三角形,又因为BC2+?AC2=AB2,?△ACB为等腰直角三角形,所以∠ABC=45°.
7. 【答案】C【解析】∵|a-12|≥0,≥0,(c-20)2≥0,∴由题意得,a-12=0,?b-16=0,c-20=0,则有a=12,b=16,c=20.∵a2+b2=122+162=400=202=c2,∴该三角形为直角三角形,c为斜边.设斜边上的高为h.由面积公式得ab=ch,所以h===9.6.
8. 【答案】正北
?【解析】因为82+152=172,所以△ABC为直角三角形,即AB与BC垂直.
9. 【答案】2
?【解析】因为m+3>m+2>m+1,所以m+3为直角边,根据勾股定理得,(m+1)2+(m+2)2=(m+3)2,解得m=2或m=-2(舍去).所以m=2.
10. 【答案】如果ac>bc(c≠0),?那么a>b
?【解析】根据命题写出它的逆命题,即原命题的题设是逆命题的结论,原命题的结论是逆命题的题设.
11. 【答案】直角三角形
?【解析】∵|a-3|≥0,≥0,(c-5)2≥0,?结合题意得a-3=0,b-4=0,c-5=0.∴a=3,b=4,c=5,a2+b2=9+16=25=c2,∴△ABC是直角三角形.
12. 【答案】如图,甲船航行的距离为BM=8×2=16(海里),乙船航行的距离为BP=15×2=30(海里).
?
?∵162+302=1?156=342,∴BM2+BP2=MP2,
?∴△MBP为直角三角形,且∠MBP=90°,
?∴乙船是沿着南偏东30°的方向航行的.
?
13. 【答案】∵a+b=4,ab=1,∴(a+b)2=42=16,即a2+b2+2ab=16,
?∴a2+b2=16-2ab=16-2×1=14,又∵c2=()2=14,∴a2+b2=c2,又∵a,b,c是△ABC的三边,根据勾股定理得△ABC为直角三角形.
?
14. 【答案】连接AC(如图).
?
?∵AD⊥DC,
?∴在Rt△ACD中,由勾股定理
?得AC==5?m.
?又∵AC2+BC2=52+122=132=AB2,
?∴△ABC为直角三角形,
?∴这块地的面积为S△ABC-S△ACD=AC×BC-AD×CD=×?5×12-×4×?3=24(m2).
?
15. 【答案】因为CD2+AD2=(5)2+52=100=AC2,
?所以△ACD是直角三角形,且∠D=90°.
?在Rt△ABD中,BD==3?(dm),所以BC=BD-CD=(3-5)?dm,
?所以△ABC的面积为BC·AD=×(3-5)×5=(dm2).
?
16. 【答案】如图,作DE∥AB交BC于点E,连接BD,
?则可以证明△ABD≌△EDB(ASA),
?
?∴DE=AB=4,BE=AD=3.
?∵BC=6,∴EC=BC-BE=3,∴EC=EB.
?∵DE2+CE2=42+32=25=CD2,
?∴△DEC为直角三角形,∴∠DEC=90°.
?又∵EC=EB=3,
?∴△DBC为等腰三角形,∴DB=DC=5.
?在△BDA中,
?∵AD2+AB2=32+42=25=BD2,
?∴△BDA是直角三角形.
?易得S△BDA=×3×4=6,
?S△DBC=×6×4=12,
?∴S△四边形ABCD=S△BDA+S△DBC=6+12=18.
?
17. 【答案】在Rt△ACD和Rt△BCD中,
?∵AC2=AD2+CD2,BC2=CD2+BD2,
?∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2,
?∴△ABC是直角三角形.
?
18. 【答案】延长AD到点E,使DE=AD,连接BE.∵点D是BC的中点,∴BD=CD.在△ADC和△EDB中,CD=BD,∠ADC=∠EDB,AD=ED,∴△ADC≌△EDB,∴EB=AC=13,AE=2AD=2×6=12.又∵AB=5,∴AB2+AE2=52+122=169=132=BE2,∴△ABE是直角三角形,且∠BAE=90°,∴BA⊥AD.
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人 得分 一、选择题
1. 在△ABC中,∠A,∠B,∠C的对边分别为a,b,c且(a+b)(a-b)=c2,则( )
A. ∠A为直角?????????????B. ∠C为直角?????????????
?C. ∠B为直角?????????????D. △ABC不是直角三角形?????????????
2. 满足下列条件的三角形中,不是直角三角形的是 ( )
A. 三内角之比为1∶2∶3?????????????B. 三边长的平方之比为1∶2∶3?????????????
?C. 三边长之比为3∶4∶5?????????????D. 三内角之比为3∶4∶5?????????????
3. 下列几组数:①9,12,15,②8,15,17,③7,24,25,④n2-1,2n,n2+1(n是大于1的整数),其中是勾股数的有 ( )
A. 1组?????????????B. 2组?????????????C. 3组?????????????D. 4组?????????????
4. 以下定理,其中有逆定理的是( )
A. 对顶角相等?????????????
?B. 互为邻补角的角平分线互相垂直?????????????
?C. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补?????????????
?D. 直角三角形的两条直角边的平方和等于斜边的平方?????????????
5. 下列各组数中,是勾股数的是( )
A. 14,36,39?????????????B. 8,24,25?????????????C. 8,15,17?????????????D. 10,20,26?????????????
6. 如图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ABC的度数为?( )
?
A. 90°?????????????B. 60°?????????????C. 45°?????????????D. 30°?????????????
7. 一个三角形三边长a,b,c满足|a-12|++(c-20)2=0,则这个三角形最长边上的高为( )
A. 9.8?????????????B. 4.8?????????????C. 9.6?????????????D. 10?????????????
评卷人 得分 二、填空题
8. 如图所示,点A为小红家的位置,点B为小明家的位置,点C为学校的位置,三地之间的距离如图,已知学校在小明家的正西方向,则小红家在小明家的 方向.
?
9. 若一个三角形的三边长分别为m+1,m+2,m+3,那么当m= 时,这个三角形是直角三角形.?
10. 把命题“如果a>b,那么ac>bc(c≠0)”的逆命题改写为“如果……,那么……”的形式: ?
11. 已知a,b,c是△ABC的三边,且满足|a-3|++(c-5)2=0,则此三角形的形状是 .
评卷人 得分 三、解答题
12. 在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
13. 如图所示,已知△ABC的三边分别是a,b,c,且a+b=4,ab=1,c=,试判断△ABC的形状.
?
14. 如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
?
15. 如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
?
16. 已知:如图,在四边形ABCD中,AD∥BC,AB=4,BC=6,CD=5,AD=3.
?求四边形ABCD的面积.
?
评卷人 得分 四、证明题
17. 已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
?求证:△ABC是直角三角形.
?
18. 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,求证:BA⊥AD.
?
参考答案
1. 【答案】A【解析】因为(a+b)(a-b)=a2-b2=c2,所以b2+c2=a2.所以△ABC为直角三角形,?∠A为直角,故选A.
2. 【答案】D【解析】A项中,由三角形内角和为180°可得,三个内角分别为30°,60°,90°,故此三角形是直角三角形.B项中,令三边长分别为?a,b,c,则a2∶b2∶c2=1∶2∶3,∴a2+b2=c2,故满足此条件的三角形是直角三角形.C项中,a∶b∶c=3∶4∶5,设a=3k,则b=4k,c=5k,∴a2+b2=(3k)2+(4k)2=25k2=c2,∴是直角三角形.?D项中的最大角为75°,故不是直角三角形.
3. 【答案】D【解析】①中因为92+122=152,所以是勾股数;②中因为82+152=172,所以是勾股数;③中因为72+242=252,所以是勾股数;④中因为(n2-1)2+(2n)2=(n2+1)2,所以是勾股数.故选D.
4. 【答案】D【解析】A定理的逆命题是“相等的两个角是对顶角”,不正确;B定理的逆命题是“角平分线互相垂直的两个角是邻补角”,∵两条平行线被第三条直线所截得的同旁内角的平分线也互相垂直,∴该逆命题不成立;C定理的逆命题是“如果两个角相等或互补,那么一个角的两边与另一个角的两边分别平行”,∵当两个角相等或互补时,一个角的两边与另一个角的两边可能分别垂直,∴该逆命题不成立;D定理的逆命题为勾股定理的逆定理.综上可知A,B,C三个定理均无逆定理,故选D.
5. 【答案】C【解析】确定勾股数只需验证两小数的平方和与大数平方是否相等.
?∵142+362=1?492,392=1?521≠1?492,∴A项不是勾股数;
?∵82+242=640,252=625≠640,∴B项不是勾股数;
?∵82+152=289,172=289,∴C是勾股数;
?∵102+202=500,262=676≠500,∴D项不是勾股数.故选C.
6. 【答案】C【解析】连接AC,观察图形易知AB=,?BC=,?AC=,所以△ACB为等腰三角形,又因为BC2+?AC2=AB2,?△ACB为等腰直角三角形,所以∠ABC=45°.
7. 【答案】C【解析】∵|a-12|≥0,≥0,(c-20)2≥0,∴由题意得,a-12=0,?b-16=0,c-20=0,则有a=12,b=16,c=20.∵a2+b2=122+162=400=202=c2,∴该三角形为直角三角形,c为斜边.设斜边上的高为h.由面积公式得ab=ch,所以h===9.6.
8. 【答案】正北
?【解析】因为82+152=172,所以△ABC为直角三角形,即AB与BC垂直.
9. 【答案】2
?【解析】因为m+3>m+2>m+1,所以m+3为直角边,根据勾股定理得,(m+1)2+(m+2)2=(m+3)2,解得m=2或m=-2(舍去).所以m=2.
10. 【答案】如果ac>bc(c≠0),?那么a>b
?【解析】根据命题写出它的逆命题,即原命题的题设是逆命题的结论,原命题的结论是逆命题的题设.
11. 【答案】直角三角形
?【解析】∵|a-3|≥0,≥0,(c-5)2≥0,?结合题意得a-3=0,b-4=0,c-5=0.∴a=3,b=4,c=5,a2+b2=9+16=25=c2,∴△ABC是直角三角形.
12. 【答案】如图,甲船航行的距离为BM=8×2=16(海里),乙船航行的距离为BP=15×2=30(海里).
?
?∵162+302=1?156=342,∴BM2+BP2=MP2,
?∴△MBP为直角三角形,且∠MBP=90°,
?∴乙船是沿着南偏东30°的方向航行的.
?
13. 【答案】∵a+b=4,ab=1,∴(a+b)2=42=16,即a2+b2+2ab=16,
?∴a2+b2=16-2ab=16-2×1=14,又∵c2=()2=14,∴a2+b2=c2,又∵a,b,c是△ABC的三边,根据勾股定理得△ABC为直角三角形.
?
14. 【答案】连接AC(如图).
?
?∵AD⊥DC,
?∴在Rt△ACD中,由勾股定理
?得AC==5?m.
?又∵AC2+BC2=52+122=132=AB2,
?∴△ABC为直角三角形,
?∴这块地的面积为S△ABC-S△ACD=AC×BC-AD×CD=×?5×12-×4×?3=24(m2).
?
15. 【答案】因为CD2+AD2=(5)2+52=100=AC2,
?所以△ACD是直角三角形,且∠D=90°.
?在Rt△ABD中,BD==3?(dm),所以BC=BD-CD=(3-5)?dm,
?所以△ABC的面积为BC·AD=×(3-5)×5=(dm2).
?
16. 【答案】如图,作DE∥AB交BC于点E,连接BD,
?则可以证明△ABD≌△EDB(ASA),
?
?∴DE=AB=4,BE=AD=3.
?∵BC=6,∴EC=BC-BE=3,∴EC=EB.
?∵DE2+CE2=42+32=25=CD2,
?∴△DEC为直角三角形,∴∠DEC=90°.
?又∵EC=EB=3,
?∴△DBC为等腰三角形,∴DB=DC=5.
?在△BDA中,
?∵AD2+AB2=32+42=25=BD2,
?∴△BDA是直角三角形.
?易得S△BDA=×3×4=6,
?S△DBC=×6×4=12,
?∴S△四边形ABCD=S△BDA+S△DBC=6+12=18.
?
17. 【答案】在Rt△ACD和Rt△BCD中,
?∵AC2=AD2+CD2,BC2=CD2+BD2,
?∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2,
?∴△ABC是直角三角形.
?
18. 【答案】延长AD到点E,使DE=AD,连接BE.∵点D是BC的中点,∴BD=CD.在△ADC和△EDB中,CD=BD,∠ADC=∠EDB,AD=ED,∴△ADC≌△EDB,∴EB=AC=13,AE=2AD=2×6=12.又∵AB=5,∴AB2+AE2=52+122=169=132=BE2,∴△ABE是直角三角形,且∠BAE=90°,∴BA⊥AD.
