北师大版八年级数学下册第一章第02课 等边三角形的性质导学案(教师版)
文档属性
| 名称 | 北师大版八年级数学下册第一章第02课 等边三角形的性质导学案(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 12:35:23 | ||
图片预览



文档简介
第一章 三角形的证明
第02课 等边三角形的性质
等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质,并且等边三角形的三个内角 相等 ,每个角都等于 60° .
知识点一:运用等边三角形的性质求角的度数
例1:如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.
【解析】∵△ADE是等边三角形,
∴∠ADE=60°,AD=DE.
又∵D,E是BC的三等分点,∴BD=DE.
∴AD=BD,∴∠BAD=∠B.
∵∠ADE=∠BAD+∠B=60°,∴∠B=30°.
同理,∠C=30°.
∴∠BAC=180°-∠B-∠C=120°.
练习:如图,点C在BE上,BD是等边△ABC的中线,CE=CD,求证:DE=DB.
【解析】∵△ABC是等边三角形,BD是中线, ∴∠ABC=∠ACB=60°. ∠DBC=30°(等腰三角形三线合一). 又∵CE=CD,∴∠CDE=∠CED. 又∵∠BCD=∠CDE+∠CED, ∴,
∴∠DBC=∠DEC. ∴DB=DE(等角对等边).
知识点二:运用等边三角形的性质求证线段相等
例2:如图,D,E分别是等边三角形ABC的两边AB,AC上的点,且AD=CE.求证:CD=BE.
【解析】∵△ABC是等边三角形,
∴∠A=∠BCE=60°,AC=BC.
在△ACD和△CBE中,,
∴△ACD≌△CBE,∴CD=BE.
练习:△DAC和△EBC均是等边三角形,连AE、BD,AE与BD相等吗?请说明理由.
【解析】△ACE≌△DCB;
∵∠ACD=∠ECB=60°,∴∠ACD+∠DCE=∠ECB+∠DCE, ∴∠ACE=∠DCB, ∵在△ACE和△DCB中,,
∴△ACE≌△DCB(SAS),∴AE=BD.
1.如果一个等边三角形的边长是2,那么这个等边三角形的面积是
A.1 B.2 C. D.
【解析】如图示:
等边三角形高线即中点,,,
在中,,,
,
,故选.
2.如图,在中,,,平分,则等于
A.1 B. C. D.1.5
【解析】,,,,故选.
3.如图所示,是等边三角形,且,,则的度数为
A. B. C. D.
【解析】在和中,,,,
,.故选.
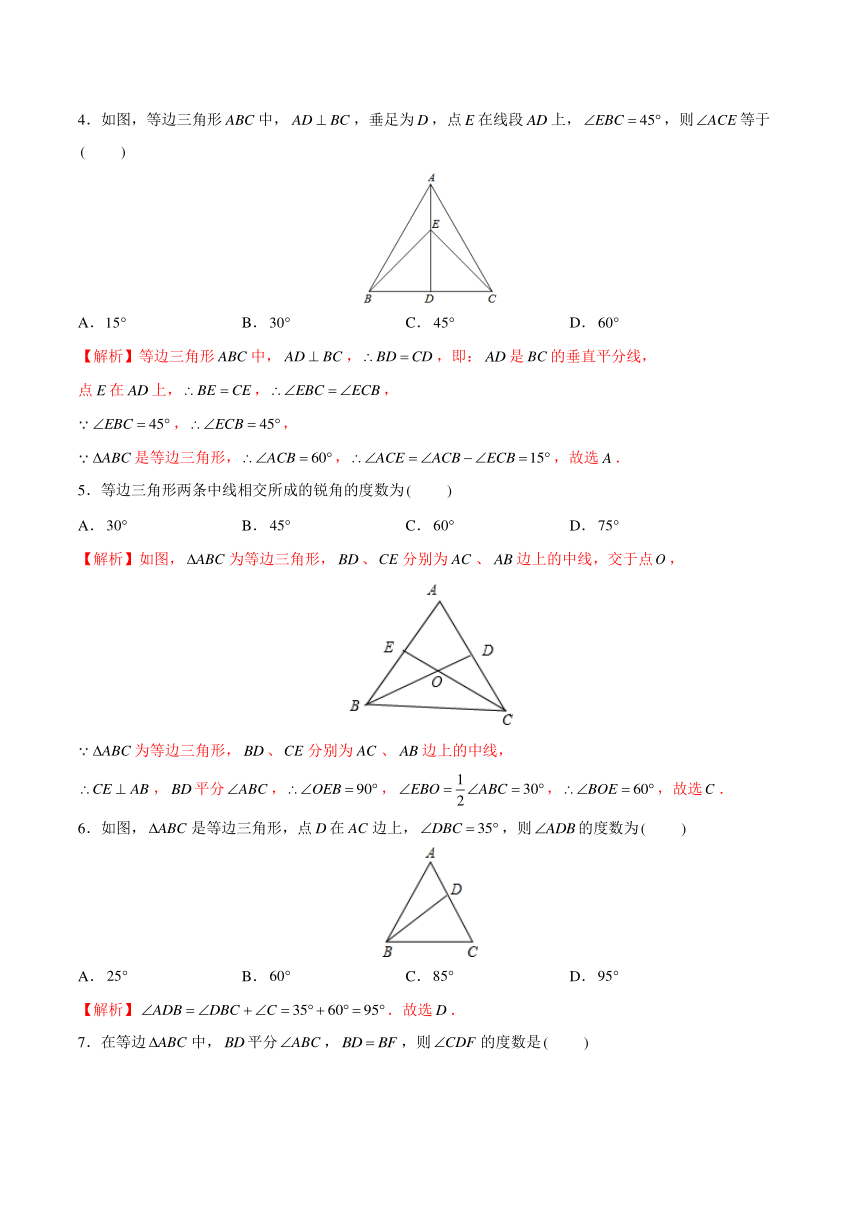
4.如图,等边三角形中,,垂足为,点在线段上,,则等于
A. B. C. D.
【解析】等边三角形中,,,即:是的垂直平分线,
点在上,,,
,,
是等边三角形,,,故选.
5.等边三角形两条中线相交所成的锐角的度数为
A. B. C. D.
【解析】如图,为等边三角形,、分别为、边上的中线,交于点,
为等边三角形,、分别为、边上的中线,
,平分,,,,故选.
6.如图,是等边三角形,点在边上,,则的度数为
A. B. C. D.
【解析】.故选.
7.在等边中,平分,,则的度数是
A. B. C. D.
【解析】在等边中,,
平分,,
,,
又等边中,平分,,,
.故选.
8.以下叙述中不正确的是
A.等边三角形的每条高线都是角平分线和中线
B.有一内角为的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,如果两个角不相等,那么它们所对的边也不相等
【解析】,正确,符合等边三角形三线合一性质;,正确,符合等边三角形的判定;
,不正确,也可能是钝角或等腰直角三角形;,正确,符合等边对等角及等角对等边的性质.故选.
9.如图,和都是边长为4的等边三角形,点,,在同一条直线上,连接,则长
A.3 B. C. D.
【解析】和都是边长为4的等边三角形,,,
又,,在中,,,,
故选.
10.在中,,过点作于,已知的周长为,则
A. B. C. D.
【解析】三角形是等边三角形,,于,,
周长为,,故选.
11.如图,正三角形的三个内角平分线交于点,则 .
【解析】为等边三角形,,
点为正三角形的三个内角平分线的交点,
,
,.故答案为.
12.,分别是等边三角形的高和中线,则与的大小关系为 .
【解析】是等边三角形,,,
平分,和重合,.故答案为:相等.
13.如图,是等边的中线,是上一点,且,则 .
【解析】是等边的中线,,,,
,,.
故答案为:15.
14.边长为4的等边三角形的面积是 .
【解析】如图,
等边三角形三线合一,为的中点,,
在中,,,,
等边的面积为.故答案为:.
15.等边三角形中,两条中线所夹的锐角的度数为 .
【解析】如图,
等边三角形,、分别是中线,、分别是角平分线,,.故答案为:.
16.等边三角形的边长为,则它的周长为 .
【解析】因为等边三角形的三边相等,而等边三角形的边长为,所以它的周长为.故答案为.
17.如图,是等边三角形,点是的中点,延长到,使,若,则 .
【解析】为等边三角形,是边的中线,
,平分,.
,.
,且为的外角,
.,
,.故答案为3.
18.如图,为等边三角形内一点,,求的度数.
【解析】是等边三角形,
,
,
,
在中,.
19.如图,等边中,是的中点,是延长线上的一点,且,,垂足是,求证:.
【解析】在等边,且是的中点,
,,
,,
,,
,
,为等腰三角形,
又,是的中点,.
20.如图,等边中,,为中点,求证:.
【解析】过作交于,于,
为中点,,,
是等边三角形,,
,, ,
,,,
,,,
,,.
第02课 等边三角形的性质
等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质,并且等边三角形的三个内角 相等 ,每个角都等于 60° .
知识点一:运用等边三角形的性质求角的度数
例1:如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.
【解析】∵△ADE是等边三角形,
∴∠ADE=60°,AD=DE.
又∵D,E是BC的三等分点,∴BD=DE.
∴AD=BD,∴∠BAD=∠B.
∵∠ADE=∠BAD+∠B=60°,∴∠B=30°.
同理,∠C=30°.
∴∠BAC=180°-∠B-∠C=120°.
练习:如图,点C在BE上,BD是等边△ABC的中线,CE=CD,求证:DE=DB.
【解析】∵△ABC是等边三角形,BD是中线, ∴∠ABC=∠ACB=60°. ∠DBC=30°(等腰三角形三线合一). 又∵CE=CD,∴∠CDE=∠CED. 又∵∠BCD=∠CDE+∠CED, ∴,
∴∠DBC=∠DEC. ∴DB=DE(等角对等边).
知识点二:运用等边三角形的性质求证线段相等
例2:如图,D,E分别是等边三角形ABC的两边AB,AC上的点,且AD=CE.求证:CD=BE.
【解析】∵△ABC是等边三角形,
∴∠A=∠BCE=60°,AC=BC.
在△ACD和△CBE中,,
∴△ACD≌△CBE,∴CD=BE.
练习:△DAC和△EBC均是等边三角形,连AE、BD,AE与BD相等吗?请说明理由.
【解析】△ACE≌△DCB;
∵∠ACD=∠ECB=60°,∴∠ACD+∠DCE=∠ECB+∠DCE, ∴∠ACE=∠DCB, ∵在△ACE和△DCB中,,
∴△ACE≌△DCB(SAS),∴AE=BD.
1.如果一个等边三角形的边长是2,那么这个等边三角形的面积是
A.1 B.2 C. D.
【解析】如图示:
等边三角形高线即中点,,,
在中,,,
,
,故选.
2.如图,在中,,,平分,则等于
A.1 B. C. D.1.5
【解析】,,,,故选.
3.如图所示,是等边三角形,且,,则的度数为
A. B. C. D.
【解析】在和中,,,,
,.故选.
4.如图,等边三角形中,,垂足为,点在线段上,,则等于
A. B. C. D.
【解析】等边三角形中,,,即:是的垂直平分线,
点在上,,,
,,
是等边三角形,,,故选.
5.等边三角形两条中线相交所成的锐角的度数为
A. B. C. D.
【解析】如图,为等边三角形,、分别为、边上的中线,交于点,
为等边三角形,、分别为、边上的中线,
,平分,,,,故选.
6.如图,是等边三角形,点在边上,,则的度数为
A. B. C. D.
【解析】.故选.
7.在等边中,平分,,则的度数是
A. B. C. D.
【解析】在等边中,,
平分,,
,,
又等边中,平分,,,
.故选.
8.以下叙述中不正确的是
A.等边三角形的每条高线都是角平分线和中线
B.有一内角为的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,如果两个角不相等,那么它们所对的边也不相等
【解析】,正确,符合等边三角形三线合一性质;,正确,符合等边三角形的判定;
,不正确,也可能是钝角或等腰直角三角形;,正确,符合等边对等角及等角对等边的性质.故选.
9.如图,和都是边长为4的等边三角形,点,,在同一条直线上,连接,则长
A.3 B. C. D.
【解析】和都是边长为4的等边三角形,,,
又,,在中,,,,
故选.
10.在中,,过点作于,已知的周长为,则
A. B. C. D.
【解析】三角形是等边三角形,,于,,
周长为,,故选.
11.如图,正三角形的三个内角平分线交于点,则 .
【解析】为等边三角形,,
点为正三角形的三个内角平分线的交点,
,
,.故答案为.
12.,分别是等边三角形的高和中线,则与的大小关系为 .
【解析】是等边三角形,,,
平分,和重合,.故答案为:相等.
13.如图,是等边的中线,是上一点,且,则 .
【解析】是等边的中线,,,,
,,.
故答案为:15.
14.边长为4的等边三角形的面积是 .
【解析】如图,
等边三角形三线合一,为的中点,,
在中,,,,
等边的面积为.故答案为:.
15.等边三角形中,两条中线所夹的锐角的度数为 .
【解析】如图,
等边三角形,、分别是中线,、分别是角平分线,,.故答案为:.
16.等边三角形的边长为,则它的周长为 .
【解析】因为等边三角形的三边相等,而等边三角形的边长为,所以它的周长为.故答案为.
17.如图,是等边三角形,点是的中点,延长到,使,若,则 .
【解析】为等边三角形,是边的中线,
,平分,.
,.
,且为的外角,
.,
,.故答案为3.
18.如图,为等边三角形内一点,,求的度数.
【解析】是等边三角形,
,
,
,
在中,.
19.如图,等边中,是的中点,是延长线上的一点,且,,垂足是,求证:.
【解析】在等边,且是的中点,
,,
,,
,,
,
,为等腰三角形,
又,是的中点,.
20.如图,等边中,,为中点,求证:.
【解析】过作交于,于,
为中点,,,
是等边三角形,,
,, ,
,,,
,,,
,,.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
