北师大版八年级数学下册第一章第03课 等腰三角形的判定与反证法导学案(教师版)
文档属性
| 名称 | 北师大版八年级数学下册第一章第03课 等腰三角形的判定与反证法导学案(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 389.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 00:00:00 | ||
图片预览





文档简介
第一章 三角形的证明
第03课 等腰三角形的判定与反证法
1.等腰三角形的判定:有两个角 相等 的三角形是等腰三角形.简述为 等校对等边 .
2.证明时,先假设命题的结论 不成立 ,然后推导出与定义、基本事实、已有定理或已知条件相 矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为 反证法 .
知识点一:等腰三角形的判定
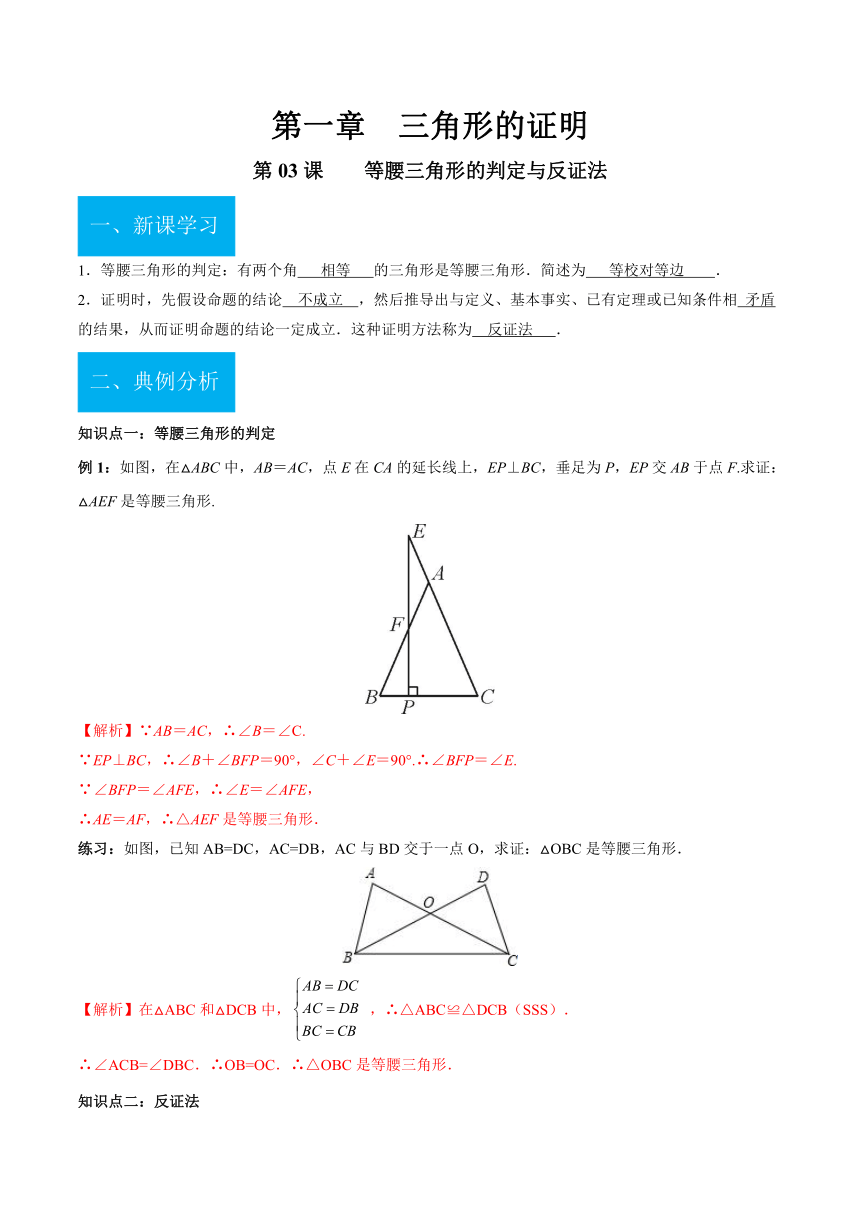
例1:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F.求证:△AEF是等腰三角形.
【解析】∵AB=AC,∴∠B=∠C.
∵EP⊥BC,∴∠B+∠BFP=90°,∠C+∠E=90°.∴∠BFP=∠E.
∵∠BFP=∠AFE,∴∠E=∠AFE,
∴AE=AF,∴△AEF是等腰三角形.
练习:如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.
【解析】在△ABC和△DCB中, ,∴△ABC≌△DCB(SSS). ∴∠ACB=∠DBC.∴OB=OC.∴△OBC是等腰三角形.
知识点二:反证法
例2:已知五个正数的和等于1,用反证法证明:这五个正数中至少有一个大于或等于.
【解析】假设这五个正数a1,a2,a3,a4,a5中没有一个大于或等于,即都小于,
那么a1+a2+a3+a4+a5<×5=1,这与a1+a2+a3+a4+a5=1相矛盾,
∴假设不成立,即原命题成立.
练习:如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
【解析】假设∠DAB是钝角或直角, ∵AB=AC,AD是底边BC上的高, ∴∠BAC=2∠DAB, ∴∠DAB是钝角或直角, ∴2∠DAB≥180°,不符合三角形内角和定理, ∴假设不成立, ∴∠DAB是一个锐角.
知识点三:等角对等边的实际应用
例3:上午8时,一条船从海岛A出发,以15n?mile/h(海里/时,1n?mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.求从海岛B到灯塔C的距离.
【解析】∵∠NBC=84°,∠NAC=42°, ∴∠C=84°-42°=42°. ∴∠C=∠NAC,∴BC=AB, ∵上午8时,一条船从海岛A出发,以150n?mile/h的速度向正北航行.10时到达海岛B处, ∴BC=AB=15×2=30n?mile.
1.如图,在中,,,和的平分线交于点,过点作分别交、于、,则的周长为
A.10 B.6 C.4 D.不确定
【解析】,.
平分,,.
,,.
同理,.
故选.
2.如图,,平分,过作交于点,若点在上,且满足,则的度数为
A. B. C.或 D.或
【解析】如图,;
平分,由图形的对称性可知:,;
,,;;
当点位于点处时,,,故选.
3.如图,在中,过顶点的直线,、的平分线分别交于点、,若,,则的长为
A.6 B.7 C.8 D.9
【解析】由分析得:,;
根据平行线的性质得:,;
所以,,则,;
所以;故选.
4.已知,如图,在中,,,是的平分线,,则图中等腰三角形一共有
A.2个 B.3个 C.4个 D.5个
【解析】,是等腰三角形;
,是等腰三角形;
是的平分线,,
,,是等腰三角形;
和为等腰三角形;图中等腰三角形的个数有5个;故选.
5.如图所示.中,,在上,,,则的度数为
A. B. C. D.
【解析】如图,,,
,,
,,即,
,.故选.
6.如图,,为的中点,以下结论正确的有几个?
①;②;③;④是的角平分线.
A.1 B.2 C.3 D.4
【解析】,为的中点,,,为公共边,
,,,,即是的角平分线.
故选.
7.如图,,且平分,过点作交于点.若点到的距离为2,则的长为
A.1 B.2 C.3 D.4
【解析】过作,,
平分,,,
,,,
,,,.故选.
8.如图,在中,,,两点分别在,上,是的平分线,,若,,则的周长是
A. B. C. D.
【解析】,平分,,,
,,,
,且,
,即的周长为,
故选.
9.已知四边形,用反证法证明“四边形中至少有一个角是直角或钝角”时,应先假设
A.四个内角都是锐角 B.四个内角都是直角或钝角
C.没有一个内角是钝角 D.没有一个内角是直角
【解析】用反证法证明“四边形中至少有一个角是直角或钝角”时第一步应假设:四个内角都是锐角.
故选.
10.用反证法证明“三角形中至少有一个内角大于或等于时,应假设
A.三角形的二个内角小于
B.三角形的三个内角都小于
C.三角形的二个内角大于
D.三角形的三个内角都大于
【解析】用反证法证明“三角形中至少有一个内角大于或等于”时,
第一步应先假设三角形的三个内角都小于,故选.
11.如图,的面积为,与的平分线垂直,垂足是点,则的面积为 .
【解析】如图,延长交于点,
垂直的平分线于,,
,,,
故答案为:1.
12.如图, 在中,,点在延长线上,于点,交于点,若,,则的长度为 .
【解析】在中,,,
,,,,
又,,,是等腰三角形 .
又,,,,.
13.如图,在中,,、分别是和的平分线,且,,则的周长是 .
【解析】、分别是和的角平分线,
,,
,,
,,
,,
,,
的周长.故答案是:8.
14.如图,在中,、分别平分、,过点,且.,,则等于 .
【解析】、分别平分、,,,
,,,
,,
,,
.故答案为:.
15.用反证法证明“多边形中至少有三个锐角”,第一步应假设 .
【解析】用反证法证“多边形中至少有三个锐角”时,第一步应假设同一多边形中最多有一个锐角.
故答案为:同一多边形中最多有一个锐角.
16.用反证法,求证:两条直线被第三条直线所截,如果内错角不相等,那么这两条直线不平行.
【解析】证明:假设这两条直线平行.
这两条直线平行,内错角相等,这与已知条件矛盾,
假设不成立.
内错角不相等,那么这两条直线不平行.
17.如图,在中,平分,于点,,,.求的长.
【解析】如图,延长交于点.
平分,.
,.
在与中,,
.,.
,.
.
,.
18.如图,在等腰三角形中,,是底边上的高,请你利用反证法证明是一个锐角.
【解析】假设是钝角或直角,
,是底边上的高,
,
是钝角或直角,
,不符合三角形内角和定理,
假设不成立,是一个锐角.
19.已知:如图,在中,,的垂直平分线交于点,交于点.
(1)求证:是等腰三角形;
(2)若,求的度数;
(3)若,的周长为24,求的周长.
【解析】(1)的垂直平分线交于点,
,是等腰三角形;
(2)是等腰三角形,,
,
;
(3)的垂直平分线交于点,,,
的周长为24,,
的周长.
第03课 等腰三角形的判定与反证法
1.等腰三角形的判定:有两个角 相等 的三角形是等腰三角形.简述为 等校对等边 .
2.证明时,先假设命题的结论 不成立 ,然后推导出与定义、基本事实、已有定理或已知条件相 矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为 反证法 .
知识点一:等腰三角形的判定
例1:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F.求证:△AEF是等腰三角形.
【解析】∵AB=AC,∴∠B=∠C.
∵EP⊥BC,∴∠B+∠BFP=90°,∠C+∠E=90°.∴∠BFP=∠E.
∵∠BFP=∠AFE,∴∠E=∠AFE,
∴AE=AF,∴△AEF是等腰三角形.
练习:如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.
【解析】在△ABC和△DCB中, ,∴△ABC≌△DCB(SSS). ∴∠ACB=∠DBC.∴OB=OC.∴△OBC是等腰三角形.
知识点二:反证法
例2:已知五个正数的和等于1,用反证法证明:这五个正数中至少有一个大于或等于.
【解析】假设这五个正数a1,a2,a3,a4,a5中没有一个大于或等于,即都小于,
那么a1+a2+a3+a4+a5<×5=1,这与a1+a2+a3+a4+a5=1相矛盾,
∴假设不成立,即原命题成立.
练习:如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
【解析】假设∠DAB是钝角或直角, ∵AB=AC,AD是底边BC上的高, ∴∠BAC=2∠DAB, ∴∠DAB是钝角或直角, ∴2∠DAB≥180°,不符合三角形内角和定理, ∴假设不成立, ∴∠DAB是一个锐角.
知识点三:等角对等边的实际应用
例3:上午8时,一条船从海岛A出发,以15n?mile/h(海里/时,1n?mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.求从海岛B到灯塔C的距离.
【解析】∵∠NBC=84°,∠NAC=42°, ∴∠C=84°-42°=42°. ∴∠C=∠NAC,∴BC=AB, ∵上午8时,一条船从海岛A出发,以150n?mile/h的速度向正北航行.10时到达海岛B处, ∴BC=AB=15×2=30n?mile.
1.如图,在中,,,和的平分线交于点,过点作分别交、于、,则的周长为
A.10 B.6 C.4 D.不确定
【解析】,.
平分,,.
,,.
同理,.
故选.
2.如图,,平分,过作交于点,若点在上,且满足,则的度数为
A. B. C.或 D.或
【解析】如图,;
平分,由图形的对称性可知:,;
,,;;
当点位于点处时,,,故选.
3.如图,在中,过顶点的直线,、的平分线分别交于点、,若,,则的长为
A.6 B.7 C.8 D.9
【解析】由分析得:,;
根据平行线的性质得:,;
所以,,则,;
所以;故选.
4.已知,如图,在中,,,是的平分线,,则图中等腰三角形一共有
A.2个 B.3个 C.4个 D.5个
【解析】,是等腰三角形;
,是等腰三角形;
是的平分线,,
,,是等腰三角形;
和为等腰三角形;图中等腰三角形的个数有5个;故选.
5.如图所示.中,,在上,,,则的度数为
A. B. C. D.
【解析】如图,,,
,,
,,即,
,.故选.
6.如图,,为的中点,以下结论正确的有几个?
①;②;③;④是的角平分线.
A.1 B.2 C.3 D.4
【解析】,为的中点,,,为公共边,
,,,,即是的角平分线.
故选.
7.如图,,且平分,过点作交于点.若点到的距离为2,则的长为
A.1 B.2 C.3 D.4
【解析】过作,,
平分,,,
,,,
,,,.故选.
8.如图,在中,,,两点分别在,上,是的平分线,,若,,则的周长是
A. B. C. D.
【解析】,平分,,,
,,,
,且,
,即的周长为,
故选.
9.已知四边形,用反证法证明“四边形中至少有一个角是直角或钝角”时,应先假设
A.四个内角都是锐角 B.四个内角都是直角或钝角
C.没有一个内角是钝角 D.没有一个内角是直角
【解析】用反证法证明“四边形中至少有一个角是直角或钝角”时第一步应假设:四个内角都是锐角.
故选.
10.用反证法证明“三角形中至少有一个内角大于或等于时,应假设
A.三角形的二个内角小于
B.三角形的三个内角都小于
C.三角形的二个内角大于
D.三角形的三个内角都大于
【解析】用反证法证明“三角形中至少有一个内角大于或等于”时,
第一步应先假设三角形的三个内角都小于,故选.
11.如图,的面积为,与的平分线垂直,垂足是点,则的面积为 .
【解析】如图,延长交于点,
垂直的平分线于,,
,,,
故答案为:1.
12.如图, 在中,,点在延长线上,于点,交于点,若,,则的长度为 .
【解析】在中,,,
,,,,
又,,,是等腰三角形 .
又,,,,.
13.如图,在中,,、分别是和的平分线,且,,则的周长是 .
【解析】、分别是和的角平分线,
,,
,,
,,
,,
,,
的周长.故答案是:8.
14.如图,在中,、分别平分、,过点,且.,,则等于 .
【解析】、分别平分、,,,
,,,
,,
,,
.故答案为:.
15.用反证法证明“多边形中至少有三个锐角”,第一步应假设 .
【解析】用反证法证“多边形中至少有三个锐角”时,第一步应假设同一多边形中最多有一个锐角.
故答案为:同一多边形中最多有一个锐角.
16.用反证法,求证:两条直线被第三条直线所截,如果内错角不相等,那么这两条直线不平行.
【解析】证明:假设这两条直线平行.
这两条直线平行,内错角相等,这与已知条件矛盾,
假设不成立.
内错角不相等,那么这两条直线不平行.
17.如图,在中,平分,于点,,,.求的长.
【解析】如图,延长交于点.
平分,.
,.
在与中,,
.,.
,.
.
,.
18.如图,在等腰三角形中,,是底边上的高,请你利用反证法证明是一个锐角.
【解析】假设是钝角或直角,
,是底边上的高,
,
是钝角或直角,
,不符合三角形内角和定理,
假设不成立,是一个锐角.
19.已知:如图,在中,,的垂直平分线交于点,交于点.
(1)求证:是等腰三角形;
(2)若,求的度数;
(3)若,的周长为24,求的周长.
【解析】(1)的垂直平分线交于点,
,是等腰三角形;
(2)是等腰三角形,,
,
;
(3)的垂直平分线交于点,,,
的周长为24,,
的周长.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
