北师大版八年级数学下册第一章 第06课 直角三角形全等的判定定理和性质导学案(教师版)
文档属性
| 名称 | 北师大版八年级数学下册第一章 第06课 直角三角形全等的判定定理和性质导学案(教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 300.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 12:40:51 | ||
图片预览



文档简介
第一章 三角形的证明
第06课 直角三角形全等的判定定理和性质
定理:斜边和一条直角边分别____相等____的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.
知识点一:用“HL”判定两个直角三角形全等
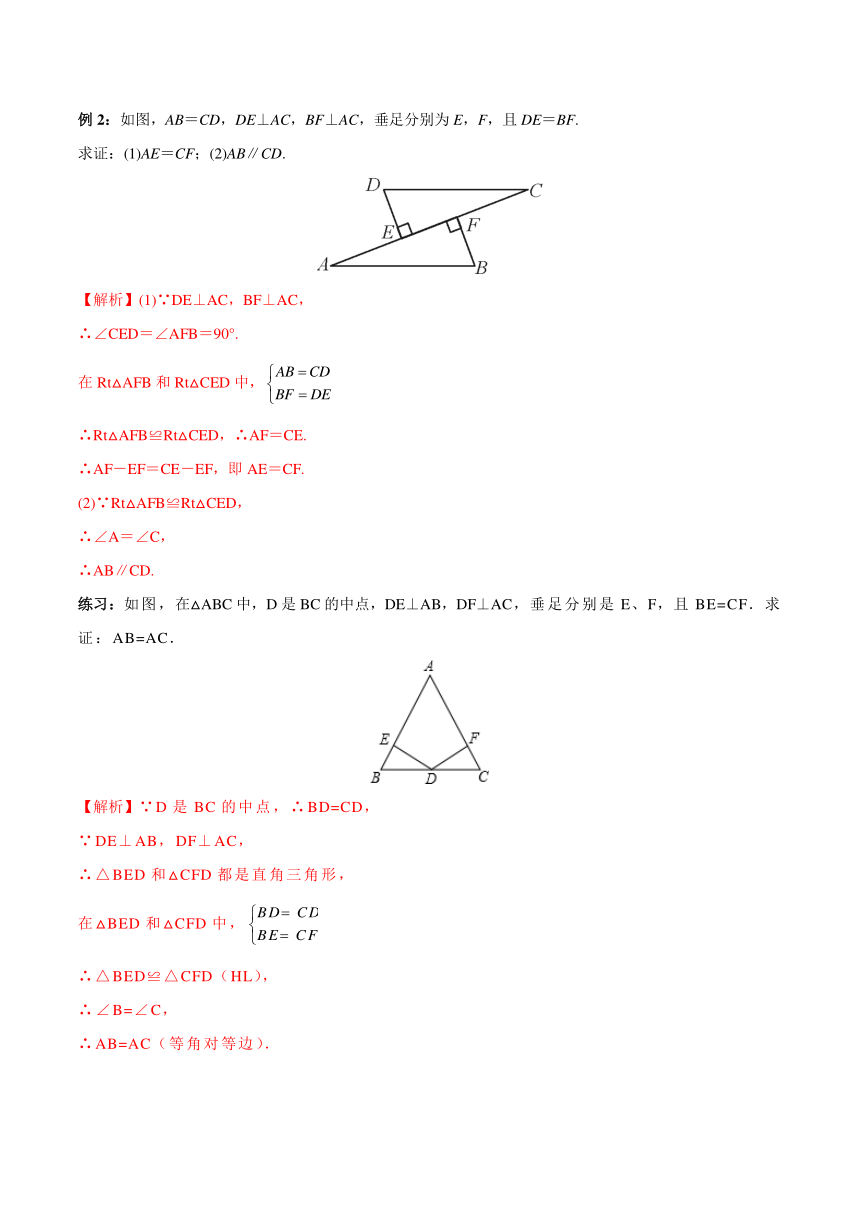
例1:如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
【解析】∵BD,CE分别是△ABC的高,∴∠BEC=∠CDB=90°,
在Rt△BEC和Rt△CDB中,,
∴Rt△BEC≌Rt△CDB(HL).
练习:如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
【解析】在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
知识点二:直角三角形全等的判定与性质的综合
例2:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.
求证:(1)AE=CF;(2)AB∥CD.
【解析】(1)∵DE⊥AC,BF⊥AC,
∴∠CED=∠AFB=90°.
在Rt△AFB和Rt△CED中,
∴Rt△AFB≌Rt△CED,∴AF=CE.
∴AF-EF=CE-EF,即AE=CF.
(2)∵Rt△AFB≌Rt△CED,
∴∠A=∠C,
∴AB∥CD.
练习:如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且BE=CF.求证:AB=AC.
【解析】∵D是BC的中点,∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BED和△CFD都是直角三角形,
在△BED和△CFD中,
∴△BED≌△CFD(HL),
∴∠B=∠C,
∴AB=AC(等角对等边).
1.下列条件中不能判定两个直角三角形全等的是
A.两个锐角分别对应相等 B.两条直角边分别对应相等
C.一条直角边和斜边分别对应相等 D.一个锐角和一条斜边分别对应相等
【解析】、两个锐角对应相等,不能说明两三角形能够完全重合,符合题意;、可以利用边角边判定两三角形全等,不符合题意;、可以利用边角边或判定两三角形全等,不符合题意;、可以利用角角边判定两三角形全等,不符合题意.故选.
2.下列说法正确的是
A.顶角和底边对应相等的两个等腰三角形全等
B.两边和一角对应相等的两个三角形全等
C.周长相等的两个三角形全等
D.斜边对应相等的两个直角三角形全等
【解析】、根据全等三角形的判定定理可以判定两个等腰三角形全等,故本选项符合题意.
、该角是两边的夹角时方可推知这两个三角形全等,负责不能推知全等,故本选项不符合题意.
、周长相等的两个三角形的大小和形状不一定相同,不能判断全等,故本选项不符合题意.
、斜边对应相等的两个直角三角形的两直角边不一定对应相等,不能判断全等,故本选项不符合题意.
故选.
3.如图所示,在中,,则为
A. B. C. D.
【解析】如图所示,在中,,则..所以,即为.故选.
4.在直角三角形中,有一个锐角是另一个锐角的2倍,则这个锐角的度数是
A. B. C. D.
【解析】设一个锐角的度数为,则另一个锐角的度数为,则,解得,,故选.
5.如图,,,垂足分别为、,、相交于点.如果,那么图中全等的直角三角形的对数是
A.1 B.2 C.3 D.4
【解析】,,,
在和中,,;,,
,,
在和中,,;,,
在和中,,;
共有3对全等三角形,故选.
6.如图,,,,要根据“”证明,则还要添加一个条件是
A. B. C. D.
【解析】条件是,
理由是:,,,
在和中,,,故选.
7.如图所示,在中,,,,则的度数为
A. B. C. D.
【解析】在中,,,,
,,,故选.
8.在中,,,是角平分线,的度数是
A. B. C. D.
【解析】,,,
平分,,,故选.
9.如图,在中,,点、为直角边、的中点,且,,则
A. B. C. D.5
【解析】设,,
,,,则有,解得,,
,故选.
10.如图,中,,,的平分线交于点,平分.给出下列结论:①; ②; ③;④.正确结论有
A.1个 B.2个 C.3个 D.4个
【解析】,,,,,故①正确;
是的平分线,,,,
,又(对顶角相等),,故②正确;
,只有时,故③错误;
,,平分,,故④正确.
综上所述,正确的结论是①②④.故选.
11.如图,中,于,要使,若根据“”判定,还需加条件 .
【解析】还需添加条件,
于,,
在和中,,,故答案为:.
12.如图,在和中,,,与交于点,则有△ △ ,其判定依据是 ,还有△ △ ,其判定依据是 .
【解析】在和中,,,是和的公共边,根据,;
由(已证)得,在 和 中,,(对顶角),
依据是可判定.故答案为:;;;;.
13.已知直角三角形一个角为,则这个三角形最小的角为 .
【解析】这个三角形最小的角,故答案为:.
14.在直角三角形中,一个锐角为,则另一个锐角等于 .
【解析】在直角三角形中,一个锐角为,则另一个锐角等于.故答案为52.
15.如图,在中,,将折叠,使点落在边上的点处,折痕为;若,则 .
【解析】与关于成轴对称,,
,,
,,故答案为:39.
16.如图,已知在和中,,判断和是否全等.
解:在和中,,,.
上面的解答过程正确吗?若不正确,请你说明错误的原因.
【解析】不正确,
在中是斜边,在中是直角边,
不满足斜边和一条直角边分别相等的两个直角三角形全等的条件,
解答过程不正确.
17.在四边形中,,于,于,,.求证:.
【解析】如图,
在与中,,
,.
又于,于,,
在与中,,.
18.在中,.现给出以下3个关系:①垂直于,②平分,③,请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
【解析】①②③.
理由:,,
,,
,平分,,
,,.
第06课 直角三角形全等的判定定理和性质
定理:斜边和一条直角边分别____相等____的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.
知识点一:用“HL”判定两个直角三角形全等
例1:如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
【解析】∵BD,CE分别是△ABC的高,∴∠BEC=∠CDB=90°,
在Rt△BEC和Rt△CDB中,,
∴Rt△BEC≌Rt△CDB(HL).
练习:如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
【解析】在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
知识点二:直角三角形全等的判定与性质的综合
例2:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.
求证:(1)AE=CF;(2)AB∥CD.
【解析】(1)∵DE⊥AC,BF⊥AC,
∴∠CED=∠AFB=90°.
在Rt△AFB和Rt△CED中,
∴Rt△AFB≌Rt△CED,∴AF=CE.
∴AF-EF=CE-EF,即AE=CF.
(2)∵Rt△AFB≌Rt△CED,
∴∠A=∠C,
∴AB∥CD.
练习:如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且BE=CF.求证:AB=AC.
【解析】∵D是BC的中点,∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BED和△CFD都是直角三角形,
在△BED和△CFD中,
∴△BED≌△CFD(HL),
∴∠B=∠C,
∴AB=AC(等角对等边).
1.下列条件中不能判定两个直角三角形全等的是
A.两个锐角分别对应相等 B.两条直角边分别对应相等
C.一条直角边和斜边分别对应相等 D.一个锐角和一条斜边分别对应相等
【解析】、两个锐角对应相等,不能说明两三角形能够完全重合,符合题意;、可以利用边角边判定两三角形全等,不符合题意;、可以利用边角边或判定两三角形全等,不符合题意;、可以利用角角边判定两三角形全等,不符合题意.故选.
2.下列说法正确的是
A.顶角和底边对应相等的两个等腰三角形全等
B.两边和一角对应相等的两个三角形全等
C.周长相等的两个三角形全等
D.斜边对应相等的两个直角三角形全等
【解析】、根据全等三角形的判定定理可以判定两个等腰三角形全等,故本选项符合题意.
、该角是两边的夹角时方可推知这两个三角形全等,负责不能推知全等,故本选项不符合题意.
、周长相等的两个三角形的大小和形状不一定相同,不能判断全等,故本选项不符合题意.
、斜边对应相等的两个直角三角形的两直角边不一定对应相等,不能判断全等,故本选项不符合题意.
故选.
3.如图所示,在中,,则为
A. B. C. D.
【解析】如图所示,在中,,则..所以,即为.故选.
4.在直角三角形中,有一个锐角是另一个锐角的2倍,则这个锐角的度数是
A. B. C. D.
【解析】设一个锐角的度数为,则另一个锐角的度数为,则,解得,,故选.
5.如图,,,垂足分别为、,、相交于点.如果,那么图中全等的直角三角形的对数是
A.1 B.2 C.3 D.4
【解析】,,,
在和中,,;,,
,,
在和中,,;,,
在和中,,;
共有3对全等三角形,故选.
6.如图,,,,要根据“”证明,则还要添加一个条件是
A. B. C. D.
【解析】条件是,
理由是:,,,
在和中,,,故选.
7.如图所示,在中,,,,则的度数为
A. B. C. D.
【解析】在中,,,,
,,,故选.
8.在中,,,是角平分线,的度数是
A. B. C. D.
【解析】,,,
平分,,,故选.
9.如图,在中,,点、为直角边、的中点,且,,则
A. B. C. D.5
【解析】设,,
,,,则有,解得,,
,故选.
10.如图,中,,,的平分线交于点,平分.给出下列结论:①; ②; ③;④.正确结论有
A.1个 B.2个 C.3个 D.4个
【解析】,,,,,故①正确;
是的平分线,,,,
,又(对顶角相等),,故②正确;
,只有时,故③错误;
,,平分,,故④正确.
综上所述,正确的结论是①②④.故选.
11.如图,中,于,要使,若根据“”判定,还需加条件 .
【解析】还需添加条件,
于,,
在和中,,,故答案为:.
12.如图,在和中,,,与交于点,则有△ △ ,其判定依据是 ,还有△ △ ,其判定依据是 .
【解析】在和中,,,是和的公共边,根据,;
由(已证)得,在 和 中,,(对顶角),
依据是可判定.故答案为:;;;;.
13.已知直角三角形一个角为,则这个三角形最小的角为 .
【解析】这个三角形最小的角,故答案为:.
14.在直角三角形中,一个锐角为,则另一个锐角等于 .
【解析】在直角三角形中,一个锐角为,则另一个锐角等于.故答案为52.
15.如图,在中,,将折叠,使点落在边上的点处,折痕为;若,则 .
【解析】与关于成轴对称,,
,,
,,故答案为:39.
16.如图,已知在和中,,判断和是否全等.
解:在和中,,,.
上面的解答过程正确吗?若不正确,请你说明错误的原因.
【解析】不正确,
在中是斜边,在中是直角边,
不满足斜边和一条直角边分别相等的两个直角三角形全等的条件,
解答过程不正确.
17.在四边形中,,于,于,,.求证:.
【解析】如图,
在与中,,
,.
又于,于,,
在与中,,.
18.在中,.现给出以下3个关系:①垂直于,②平分,③,请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
【解析】①②③.
理由:,,
,,
,平分,,
,,.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
