北师大版八年级数学下册第一章 第09课 垂直平分线的应用导学案(教师版)
文档属性
| 名称 | 北师大版八年级数学下册第一章 第09课 垂直平分线的应用导学案(教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 12:47:23 | ||
图片预览



文档简介
第一章 三角形的证明
第09课 三角形中的垂直平分线
1.三角形三条边的垂直平分线的性质:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
2.尺规作等腰三角形的步骤:
(1)写出已知和求作;(2)写出作法(比较复杂的作图题,在作图之前需进行分析).
知识点一:三角形三条边的垂直平分线的性质
例1:如图,有A,B,C三个村庄,现要修建一所希望小学,使三个村庄到学校的距离相等,学校的地址应选在什么地方?请你在图中画出学校的位置并说明理由(保留作图痕迹).
【解析】设A,B,C为顶点构建三角形,作任意两边的中垂线,交于点O,O点即是学校的位置.
理由:线段垂直平分线上的点到两顶点的距离相等,由作图可知,OA=OB,OB=OC,
∴OA=OC,则学校建在O处,三个村庄到学校的距离相等.
练习:如图:某山区有三个村庄A、B、C,现在要建一座希望小学,使三个村庄的孩子上学所走的路程一样,学校的位置应选在( )
A.△ABC三个角平分线的交点 B.△ABC三条边的中垂线的交点
C.△ABC三条中线的交点 D.△ABC三条高所在直线的交点
【解析】∵使三个村庄的孩子上学所走的路程一样,∴学校的位置应选在△ABC三条边的中垂线的交点.
故选B.
知识点二 角平分线与线段垂直平分线的性质的综合运用
例2:如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.
【解析】连接BD,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,∴DM=DN,
∵DE垂直平分线BC,∴DB=DC,
在Rt△DMB和Rt△DNC中,
∴Rt△DMB≌Rt△DNC(HL),∴BM=CN.
练习:如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:AD垂直平分EF.
【解析】∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△ADE和Rt△ADF中, ,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,又DE=DF,
∴AD垂直平分EF(到线段两端点的距离相等的点一定在线段的垂直平分线上).
1.在中,,有一点同时满足以下三个条件:①在直角边上;②在的角平分线上;③在斜边的垂直平分线上,那么为
A. B. C. D.
【解析】在直角边的垂直平分线上,,,
在的角平分线上,,,故选.
2.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
【解析】,,
的垂直平分线交边于点,的垂直平分线交边于点,
,,,,
,
.故选.
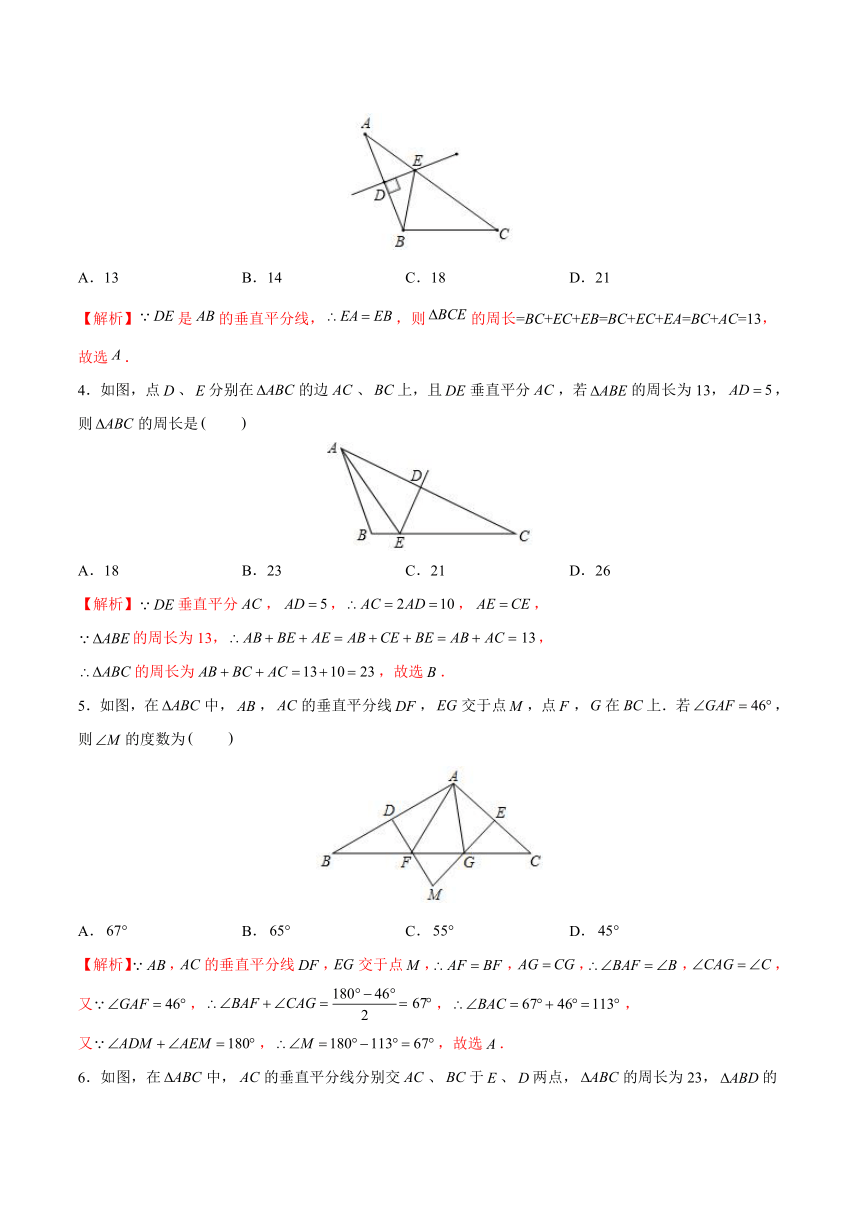
3.如图,中,,,的垂直平分线交于点,交边于点,则的周长为
A.13 B.14 C.18 D.21
【解析】是的垂直平分线,,则的周长=BC+EC+EB=BC+EC+EA=BC+AC=13,故选.
4.如图,点、分别在的边、上,且垂直平分,若的周长为13,,则的周长是
A.18 B.23 C.21 D.26
【解析】垂直平分,,,,
的周长为13,,
的周长为,故选.
5.如图,在中,,的垂直平分线,交于点,点,在上.若,则的度数为
A. B. C. D.
【解析】,的垂直平分线,交于点,,,,,又,,,
又,,故选.
6.如图,在中,的垂直平分线分别交、于、两点,的周长为23,的周长为15,则的长是
A.6 B.8 C.12 D.16
【解析】的垂直平分线分别交、于、两点,,
的周长为23,的周长为15,,,
,,故选.
7.已知:如图,垂直平分,的周长是,,则的周长是
A. B. C. D.
【解析】中,垂直平分,,故可得出,
,的周长.故选.
8.如图所示,线段,的垂直平分线相交于点,则与的关系是
A. B. C. D.
【解析】连接,
线段,的垂直平分线相交于点,,,,故选.
9.已知,如图,在中,,边上的垂直平分线交于点,交于点,,的周长为,则的长是 .
【解析】是的垂直平分线,,
的周长,
,的周长为,,解得,故答案为:.
10.如图,点为的平分线上一点,过任作一直线分别与的两边交于,两点,为中点,过作的垂线交于点,,则 .
【解析】如图:过作于,于,则,
平分,,为中点,,,
在和中,,,
,.
,;
故答案为:.
11.如图,在中,,的垂直平分线交于点,,若,则 .
【解析】在中,,的垂直平分线交于点,,
,,,,
,,,
,
故答案为:.
12.如图,在中,边的垂直平分线交边于点,若厘米,厘米,则的周长为 14 .
【解析】边的垂直平分线交边于点,,
厘米,厘米,
的周长为厘米厘米厘米,
故答案为:14.
13.作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点,表示大学,,表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
【解析】(1)连接,分别以、为圆心,以大于为半径画圆,两圆相交于,连接,则即为线段的垂直平分线;
(2)以为圆心,以任意长为半径画圆,分别交、于、,再分别以、为圆心,以大于为半径画圆,两圆相交于,连接,则即为的平分线(或的外角平分线);
(3)与相交于点,则点即为所求.如图所示:
14.如图,在中,度.
(1)用圆规和直尺在上作点,使点到、的距离相等;(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点到、的距离相等时,求的度数.
【解析】(1)
(2)连接.
点到、的距离相等,是的平分线,.
又点在线段的垂直平分线上,,
. .
15.如图,在中,,平分,于点交于点,平分,交于点,交于点.求证:线段垂直平分线段.
【解析】,,
,,
,,
平分,,,
,,,
平分,,,即线段垂直平分线段.
16.如图,点为三边垂直平分线的交点,,,
(1)求的度数;
(2)直接写出与的数量关系 .
【解析】(1)为三边垂直平分线的交点,
,,,
,.
(2),,
.故答案为.
第09课 三角形中的垂直平分线
1.三角形三条边的垂直平分线的性质:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
2.尺规作等腰三角形的步骤:
(1)写出已知和求作;(2)写出作法(比较复杂的作图题,在作图之前需进行分析).
知识点一:三角形三条边的垂直平分线的性质
例1:如图,有A,B,C三个村庄,现要修建一所希望小学,使三个村庄到学校的距离相等,学校的地址应选在什么地方?请你在图中画出学校的位置并说明理由(保留作图痕迹).
【解析】设A,B,C为顶点构建三角形,作任意两边的中垂线,交于点O,O点即是学校的位置.
理由:线段垂直平分线上的点到两顶点的距离相等,由作图可知,OA=OB,OB=OC,
∴OA=OC,则学校建在O处,三个村庄到学校的距离相等.
练习:如图:某山区有三个村庄A、B、C,现在要建一座希望小学,使三个村庄的孩子上学所走的路程一样,学校的位置应选在( )
A.△ABC三个角平分线的交点 B.△ABC三条边的中垂线的交点
C.△ABC三条中线的交点 D.△ABC三条高所在直线的交点
【解析】∵使三个村庄的孩子上学所走的路程一样,∴学校的位置应选在△ABC三条边的中垂线的交点.
故选B.
知识点二 角平分线与线段垂直平分线的性质的综合运用
例2:如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.
【解析】连接BD,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,∴DM=DN,
∵DE垂直平分线BC,∴DB=DC,
在Rt△DMB和Rt△DNC中,
∴Rt△DMB≌Rt△DNC(HL),∴BM=CN.
练习:如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:AD垂直平分EF.
【解析】∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△ADE和Rt△ADF中, ,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,又DE=DF,
∴AD垂直平分EF(到线段两端点的距离相等的点一定在线段的垂直平分线上).
1.在中,,有一点同时满足以下三个条件:①在直角边上;②在的角平分线上;③在斜边的垂直平分线上,那么为
A. B. C. D.
【解析】在直角边的垂直平分线上,,,
在的角平分线上,,,故选.
2.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
【解析】,,
的垂直平分线交边于点,的垂直平分线交边于点,
,,,,
,
.故选.
3.如图,中,,,的垂直平分线交于点,交边于点,则的周长为
A.13 B.14 C.18 D.21
【解析】是的垂直平分线,,则的周长=BC+EC+EB=BC+EC+EA=BC+AC=13,故选.
4.如图,点、分别在的边、上,且垂直平分,若的周长为13,,则的周长是
A.18 B.23 C.21 D.26
【解析】垂直平分,,,,
的周长为13,,
的周长为,故选.
5.如图,在中,,的垂直平分线,交于点,点,在上.若,则的度数为
A. B. C. D.
【解析】,的垂直平分线,交于点,,,,,又,,,
又,,故选.
6.如图,在中,的垂直平分线分别交、于、两点,的周长为23,的周长为15,则的长是
A.6 B.8 C.12 D.16
【解析】的垂直平分线分别交、于、两点,,
的周长为23,的周长为15,,,
,,故选.
7.已知:如图,垂直平分,的周长是,,则的周长是
A. B. C. D.
【解析】中,垂直平分,,故可得出,
,的周长.故选.
8.如图所示,线段,的垂直平分线相交于点,则与的关系是
A. B. C. D.
【解析】连接,
线段,的垂直平分线相交于点,,,,故选.
9.已知,如图,在中,,边上的垂直平分线交于点,交于点,,的周长为,则的长是 .
【解析】是的垂直平分线,,
的周长,
,的周长为,,解得,故答案为:.
10.如图,点为的平分线上一点,过任作一直线分别与的两边交于,两点,为中点,过作的垂线交于点,,则 .
【解析】如图:过作于,于,则,
平分,,为中点,,,
在和中,,,
,.
,;
故答案为:.
11.如图,在中,,的垂直平分线交于点,,若,则 .
【解析】在中,,的垂直平分线交于点,,
,,,,
,,,
,
故答案为:.
12.如图,在中,边的垂直平分线交边于点,若厘米,厘米,则的周长为 14 .
【解析】边的垂直平分线交边于点,,
厘米,厘米,
的周长为厘米厘米厘米,
故答案为:14.
13.作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点,表示大学,,表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
【解析】(1)连接,分别以、为圆心,以大于为半径画圆,两圆相交于,连接,则即为线段的垂直平分线;
(2)以为圆心,以任意长为半径画圆,分别交、于、,再分别以、为圆心,以大于为半径画圆,两圆相交于,连接,则即为的平分线(或的外角平分线);
(3)与相交于点,则点即为所求.如图所示:
14.如图,在中,度.
(1)用圆规和直尺在上作点,使点到、的距离相等;(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点到、的距离相等时,求的度数.
【解析】(1)
(2)连接.
点到、的距离相等,是的平分线,.
又点在线段的垂直平分线上,,
. .
15.如图,在中,,平分,于点交于点,平分,交于点,交于点.求证:线段垂直平分线段.
【解析】,,
,,
,,
平分,,,
,,,
平分,,,即线段垂直平分线段.
16.如图,点为三边垂直平分线的交点,,,
(1)求的度数;
(2)直接写出与的数量关系 .
【解析】(1)为三边垂直平分线的交点,
,,,
,.
(2),,
.故答案为.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
