2.3数学归纳法(共42张PPT)
文档属性
| 名称 | 2.3数学归纳法(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
新课导入
通过对n=1,2,3,4前4项的归纳,我们已经猜出其通项公式为
这个猜想对前4项成立,但是,能肯定它对后续的项也成立吗?
这个猜想需要证明,自然地,我们会想到从n=5开始一个个往下验证.
这个方法可行吗?
我们来分析此方法:
一般来说,与正整数n有关的命题,当n比较小时可以逐个验证,但当n比较大时,验证起来会很麻烦.特别是证明n取所有正整数都成立的命题时,逐一验证是不可能的.因此,从n=5开始逐个往下验证的想法价值不大.我们需要另辟蹊径,寻求一种方法:通过有限个步骤的推理,证明n取所有正整数都成立.
大家都听说过多米诺骨牌游戏,这是一种码放骨牌的游戏,码放时保证任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块骨牌也倒下.只要推到第一块骨牌,由于第一块骨牌倒下,就可导致第二块骨牌倒下;而第二块骨牌倒下,就可导致第三块骨牌倒下……最后,不论有多少块骨牌,都能全部倒下.
这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
思考…
动动脑
大家想一想,自己总结出倒下的条件.
只要满足以下两个条件,所有多米诺骨牌就都能倒下:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下;
你认为条件(2)的作用是什么?
可以看出,条件(2)事实上给出了一个递推关系:当第k块倒下时,相邻的第k+1块也倒下.
这样,只要第一块骨牌倒下,其他所有的骨牌就能够相继倒下.事实上,无论有多少块骨牌,只要保证(1)(2)成立,那么所有的骨牌一定可以全部倒下.
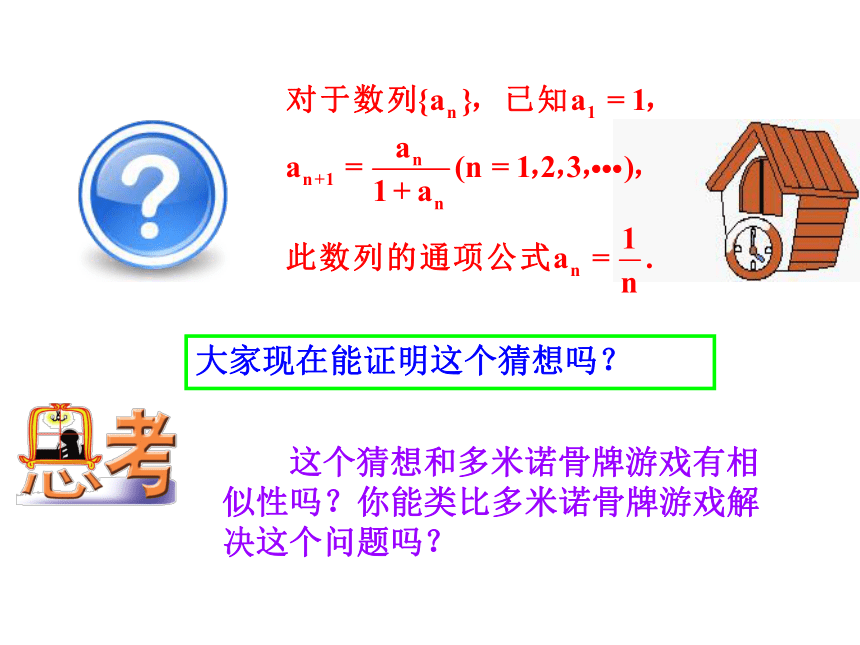
大家现在能证明这个猜想吗?
这个猜想和多米诺骨牌游戏有相似性吗?你能类比多米诺骨牌游戏解决这个问题吗?
游戏的条件(1)
由条件容易知道,n=1时猜想成立.
游戏的条件(2)
下面我们证明此猜想:
相当于
类比
证明一个递推关系.
考虑
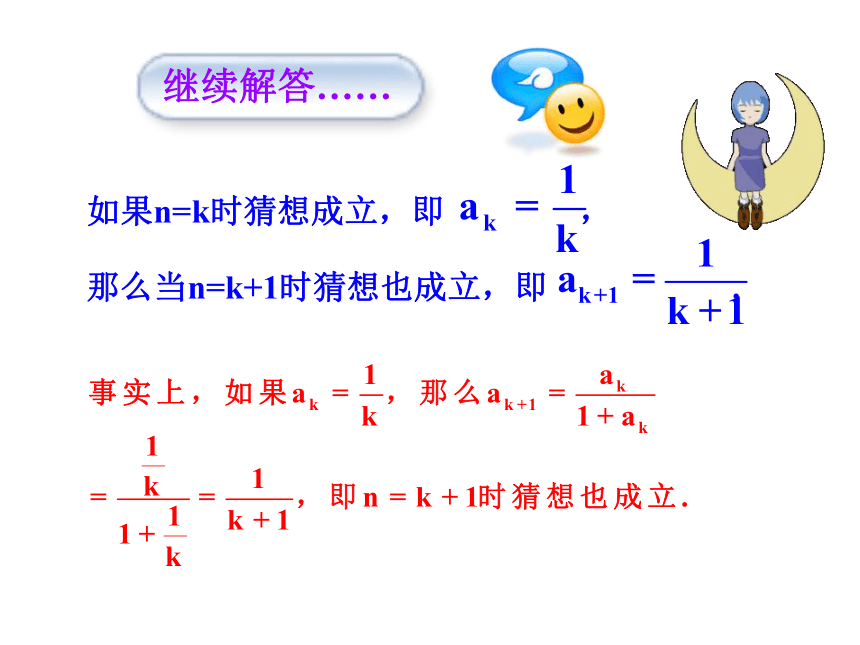
如果n=k时猜想成立,即 ,
那么当n=k+1时猜想也成立,即 .
这样,对于猜想,由已知n=1成立,就有n=2也成立;n=2成立,就有n=3也成立; n=3成立,就有n=4也成立; n=4成立,就有n=5也成立······所以,对任意的正整数n,猜想都成立.
此猜想正确,即
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
证明当n取第一个值n0 时命题成立;
2.假设当n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立.
这种证明方法就叫做
数学归纳法.
归纳奠基
归纳递推
用框图来表示此证明方法:
验证n=n0 时命题成立.
当n=k(k≥n0)时命题成立,证明n=k+1时命题也成立.
归纳奠基
归纳递推
命题对从n0开始所有的正整数n都成立.
用数学归纳法证题时,应注意的事项 :
“归纳奠基”和“归纳递推”两个步骤缺一不可,其中第一步是命题递推的基础,第二步是命题递推的根据.
具体说明如下:
(1)第一步——归纳奠基
必须有第一步,如果没有第一步,证明不可靠;
很重要哦!特别注意!
用数学归纳法进行证明时,第一步从n等于几开始,要根据具体问题而定.
如果要证明的命题是对全体正整数都成立的,则要从n=1证起;
一般来说
如果要证明的命题是对全体自然数(包括0)都成立的,则要从n=0证起.
(2)第二步——归纳递推
“假设n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立”,其本质是证明一个递推关系,归纳递推的作用是从前往后传递,有了这种向后传递的关系,就能从一个起点(例如n=1)不断发展,以至无穷.如果没有它,即使前面验证了命题对许多正整数n都成立,也不能保证命题对后面的所有正整数都成立.
用数学归纳法证明命题时,难点和关键都在第二步,而第二步主要在于合理运用归纳假设,即以“n=k时命题成立”为条件,结合其他数学知识,证明“当n=k+1时命题成立”.不能不使用“n=k时命题成立”这个条件,而直接将n=k+1代入命题,便断言此时命题成立因为这样的“证明”并不推出递推关系:
n=k时命题成立
n=k+1时命题也成立.
数学归纳法的适用范围:
数学归纳法一般被用于证明某些与正整数n(n取无限多个值)有关的数学命题,但是,并不能简单地说所有与正整数n(n取无限多个值)有关的数学命题都可以用数学归纳法证明,一般说,从n=k时的情形过渡到n=k+1时的情形,如果问题中存在可利用的递推关系,则数学归纳法有用武之地,否则使用数学归纳法就有困难.
用数学归纳法证明
证明的关键是,如何从n=k时的情形过渡到n=k+1时的情形,即:要证明n=k+1时等式成立,应如何利用n=k时等式成立这个假设.
根据(1)和(2),可知等式对任何正整数都成立.
这句是不可缺少的!
(2)用数学归纳法证明时,要注意从n=k时的情形到n=k+1时的情形是怎样过渡的,即要证明n=k+1时等式成立,应如何利用n=k时等式成立这个假设.
解:
可以看到,上面表示四个结果的分数中,分子与项数n一致,分母可用项数n表示为3n+1,于是可以猜想
下面我们用数学归纳法证明这个猜想.
根据(1)和(2),可知等式对任何正整数都成立.
课堂小结
1.数学归纳法的概念:
证明当n取第一个值n0 时命题成立;
假设当n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立.
2.数学归纳法两个步骤间的关系:
“第一步——归纳奠基和第二步——归纳递推”两个步骤缺一不可,其中第一步是命题递推的基础,第二步是命题递推的根据.
3.数学归纳法的适用范围:
一般来说,数学归纳法只适用于和正整数有关的命题.
高考链接
解:
综合(ⅰ)(ⅱ)知,对一切正整数m ,不等式都成立.
随堂练习
1+a+a2
2、某个命题当n=k (k∈N )时成立,可证得当n=k+1时也成立.现在已知当n=5时该命题不成立,那么可推得( )
A. n=6时该命题不成立
B. n=6时该命题成立
C. n=4时该命题不成立
D. n=4时该命题成立
选择
C
解答题
用数学归纳法证明
证明:
(1)当n=1时,左边=1×4=4,
右边=1×22=4,等式成立.
(2)假设当n=k时,等式成立,就是
这就是说,当n=k+1时等式也成立.根据(1)和(2),可知等式对任何n∈N*都成立.
2、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)
证明:
① n=1时:左边=1+1=2,右边=21?1=2,
左边=右边,等式成立.
② 假设当n=k((k∈N )时有: (k+1)(k+2)…(k+k)=2k? 1? 3?…? (2k-1),
当n=k+1时:
新课导入
通过对n=1,2,3,4前4项的归纳,我们已经猜出其通项公式为
这个猜想对前4项成立,但是,能肯定它对后续的项也成立吗?
这个猜想需要证明,自然地,我们会想到从n=5开始一个个往下验证.
这个方法可行吗?
我们来分析此方法:
一般来说,与正整数n有关的命题,当n比较小时可以逐个验证,但当n比较大时,验证起来会很麻烦.特别是证明n取所有正整数都成立的命题时,逐一验证是不可能的.因此,从n=5开始逐个往下验证的想法价值不大.我们需要另辟蹊径,寻求一种方法:通过有限个步骤的推理,证明n取所有正整数都成立.
大家都听说过多米诺骨牌游戏,这是一种码放骨牌的游戏,码放时保证任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块骨牌也倒下.只要推到第一块骨牌,由于第一块骨牌倒下,就可导致第二块骨牌倒下;而第二块骨牌倒下,就可导致第三块骨牌倒下……最后,不论有多少块骨牌,都能全部倒下.
这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
思考…
动动脑
大家想一想,自己总结出倒下的条件.
只要满足以下两个条件,所有多米诺骨牌就都能倒下:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下;
你认为条件(2)的作用是什么?
可以看出,条件(2)事实上给出了一个递推关系:当第k块倒下时,相邻的第k+1块也倒下.
这样,只要第一块骨牌倒下,其他所有的骨牌就能够相继倒下.事实上,无论有多少块骨牌,只要保证(1)(2)成立,那么所有的骨牌一定可以全部倒下.
大家现在能证明这个猜想吗?
这个猜想和多米诺骨牌游戏有相似性吗?你能类比多米诺骨牌游戏解决这个问题吗?
游戏的条件(1)
由条件容易知道,n=1时猜想成立.
游戏的条件(2)
下面我们证明此猜想:
相当于
类比
证明一个递推关系.
考虑
如果n=k时猜想成立,即 ,
那么当n=k+1时猜想也成立,即 .
这样,对于猜想,由已知n=1成立,就有n=2也成立;n=2成立,就有n=3也成立; n=3成立,就有n=4也成立; n=4成立,就有n=5也成立······所以,对任意的正整数n,猜想都成立.
此猜想正确,即
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
证明当n取第一个值n0 时命题成立;
2.假设当n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立.
这种证明方法就叫做
数学归纳法.
归纳奠基
归纳递推
用框图来表示此证明方法:
验证n=n0 时命题成立.
当n=k(k≥n0)时命题成立,证明n=k+1时命题也成立.
归纳奠基
归纳递推
命题对从n0开始所有的正整数n都成立.
用数学归纳法证题时,应注意的事项 :
“归纳奠基”和“归纳递推”两个步骤缺一不可,其中第一步是命题递推的基础,第二步是命题递推的根据.
具体说明如下:
(1)第一步——归纳奠基
必须有第一步,如果没有第一步,证明不可靠;
很重要哦!特别注意!
用数学归纳法进行证明时,第一步从n等于几开始,要根据具体问题而定.
如果要证明的命题是对全体正整数都成立的,则要从n=1证起;
一般来说
如果要证明的命题是对全体自然数(包括0)都成立的,则要从n=0证起.
(2)第二步——归纳递推
“假设n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立”,其本质是证明一个递推关系,归纳递推的作用是从前往后传递,有了这种向后传递的关系,就能从一个起点(例如n=1)不断发展,以至无穷.如果没有它,即使前面验证了命题对许多正整数n都成立,也不能保证命题对后面的所有正整数都成立.
用数学归纳法证明命题时,难点和关键都在第二步,而第二步主要在于合理运用归纳假设,即以“n=k时命题成立”为条件,结合其他数学知识,证明“当n=k+1时命题成立”.不能不使用“n=k时命题成立”这个条件,而直接将n=k+1代入命题,便断言此时命题成立因为这样的“证明”并不推出递推关系:
n=k时命题成立
n=k+1时命题也成立.
数学归纳法的适用范围:
数学归纳法一般被用于证明某些与正整数n(n取无限多个值)有关的数学命题,但是,并不能简单地说所有与正整数n(n取无限多个值)有关的数学命题都可以用数学归纳法证明,一般说,从n=k时的情形过渡到n=k+1时的情形,如果问题中存在可利用的递推关系,则数学归纳法有用武之地,否则使用数学归纳法就有困难.
用数学归纳法证明
证明的关键是,如何从n=k时的情形过渡到n=k+1时的情形,即:要证明n=k+1时等式成立,应如何利用n=k时等式成立这个假设.
根据(1)和(2),可知等式对任何正整数都成立.
这句是不可缺少的!
(2)用数学归纳法证明时,要注意从n=k时的情形到n=k+1时的情形是怎样过渡的,即要证明n=k+1时等式成立,应如何利用n=k时等式成立这个假设.
解:
可以看到,上面表示四个结果的分数中,分子与项数n一致,分母可用项数n表示为3n+1,于是可以猜想
下面我们用数学归纳法证明这个猜想.
根据(1)和(2),可知等式对任何正整数都成立.
课堂小结
1.数学归纳法的概念:
证明当n取第一个值n0 时命题成立;
假设当n=k(k?N*,k≥n0)时命题成立,证明当n=k+1时命题也成立.
2.数学归纳法两个步骤间的关系:
“第一步——归纳奠基和第二步——归纳递推”两个步骤缺一不可,其中第一步是命题递推的基础,第二步是命题递推的根据.
3.数学归纳法的适用范围:
一般来说,数学归纳法只适用于和正整数有关的命题.
高考链接
解:
综合(ⅰ)(ⅱ)知,对一切正整数m ,不等式都成立.
随堂练习
1+a+a2
2、某个命题当n=k (k∈N )时成立,可证得当n=k+1时也成立.现在已知当n=5时该命题不成立,那么可推得( )
A. n=6时该命题不成立
B. n=6时该命题成立
C. n=4时该命题不成立
D. n=4时该命题成立
选择
C
解答题
用数学归纳法证明
证明:
(1)当n=1时,左边=1×4=4,
右边=1×22=4,等式成立.
(2)假设当n=k时,等式成立,就是
这就是说,当n=k+1时等式也成立.根据(1)和(2),可知等式对任何n∈N*都成立.
2、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)
证明:
① n=1时:左边=1+1=2,右边=21?1=2,
左边=右边,等式成立.
② 假设当n=k((k∈N )时有: (k+1)(k+2)…(k+k)=2k? 1? 3?…? (2k-1),
当n=k+1时:
