高中数学人教新课标A版选修3-1第二讲 古希腊数学 一 希腊数学的先行者(共27张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-1第二讲 古希腊数学 一 希腊数学的先行者(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 15:28:31 | ||
图片预览







文档简介
(共27张PPT)
第二讲 古希腊数学
(公元前600—600)
知识回顾
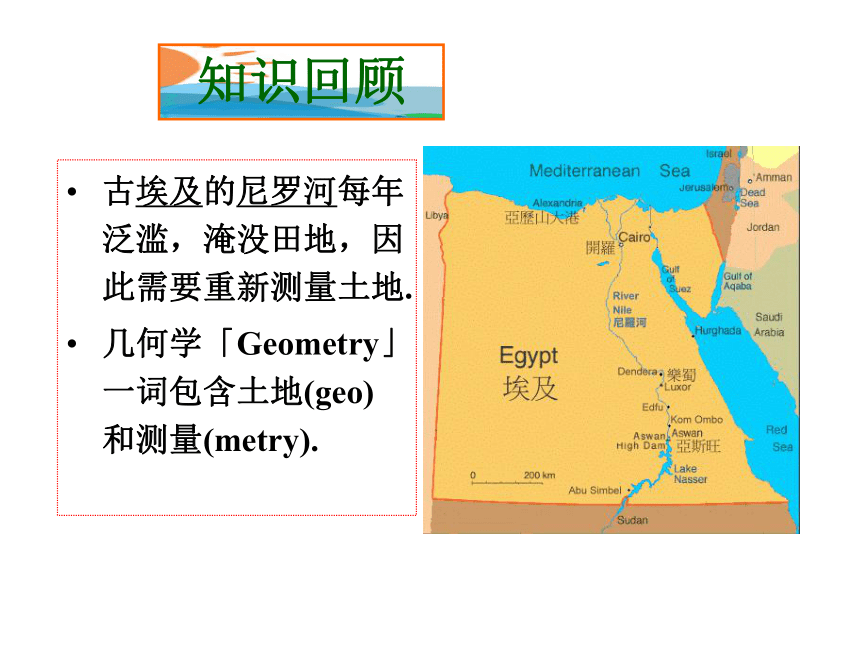
古埃及的尼罗河每年泛滥,淹没田地,因此需要重新测量土地.
几何学「Geometry」一词包含土地(geo) 和测量(metry).
古希腊包括希腊半岛、爱琴海群岛和小亚细亚西安一带.希腊文明大约可以追溯到公元前2800年,一直延续到公元600年.公元前6世纪以后,由于经济和政治的进步,自然科学和数学得到高度发展.古希腊数学指公元前700年到公元600年.
古希腊
第一阶段:从公元前700年到前323年又称为古典时期或雅典时期.即从泰勒斯的伊奥尼亚学派到柏拉图学派为止;
第二阶段:是亚历山大时期,从公元前323年欧几里德起到公元前30年是全盛时期;
希腊数学发展的历史可分为三个阶段:
第三阶段:从公元前30年到公元600年,又称为亚历山大后期—衰弱时期,即罗马人统治下的时期.
柏拉图
亚历山大大帝
导入新课
希腊的数学内容包括算术(含代数)、几何学和三角学.
古希腊人学术辩论风气较浓,都有一批学者在一二位杰出人物的领导下活动,这类组织称为学派.这时期出现了泰勒斯学派(伊奥尼亚学派)、毕达哥拉斯学派等几个著名学派以及许多著名的数学家.
数学作为一门有组织、独立的和理性的学科来说,在古希腊学者登场之前是不存在的.
---M·克莱因
一、希腊数学的先行者
论证几何的发祥人——泰勒斯是伊奥尼亚学派的创始人,是现在所知的古希腊最早的数学家、哲学家,是希腊数学的先行者.
泰勒斯 (Thales, 公元前625 - 546)曾游学古埃及,他是将古埃及的几何知识引进希腊的人.
他试图将几何结果排成逻辑链条,排在前的可推导出排在后的,因而有了「证明」的念头.
泰勒斯生于伊奥尼亚的米利 都,出身奴隶主贵族家庭,政治地位显贵,生活富足.他本人可以做官出人头地,可他却把金钱、时间和精力都全部倾注于哲学与科学,被誉为“科学之父”和“希腊数学鼻祖”.
内容介绍
多说话并不表示有才智,
去找出一件唯一智慧的东西吧,
去选择一件唯一美好的东西吧,
这样就钳住许多饶舌汉的嘴.
他献身于科学,却招来非议,为此他写了一首诗回答这些人:
泰勒斯没有著作传世,了解他只能从后人的记载中.
泰勒斯还游访过巴比伦、埃及等古代文明国家,学到了那里的数学知识和天文学知识,晚年则转向哲学,他几乎涉猎了当时人类的全部思想和活动领域,被尊为“希腊七贤”之首.
论证数学
公元前6世纪,泰勒斯去埃及,第一个将埃及人的几何学带回希腊.据说他本人发现了许多几何命题,并创立了对几何命题的逻辑推理.泰勒斯发现了如下命题:
圆被任一直径平分.
等腰三角形的两底角相等.
3.两直线相交,对顶角相等.
4.在两个三角形中,有两角一夹边对应相等,则这两个三角形完全相等.
5.半圆周角是直角.
6.相似三角形的对应边成比例.
7.三角形内角和等于两直角.
泰勒斯曾利用天文学知识、预报了发生于公元585年的一次日食,并因此消弭了一场鏖战经年的战争.
天文、测量学家
另一项令人津津乐道的业绩是在埃及时,测定了金字塔的塔高.说明他已经熟悉相似三角形的基本性质.
泰勒斯在数学方面划时代的、影响最深远的贡献是引入命题证明的思想.它标志着人类对客观事物的认识已经从实践上升到理论.是数学史上一次不寻常的飞跃.
正是有了逻辑证明,数学命题的正确性得到了保证,数学理论才立于不败之地;数学定理之间的关系得到了揭示,数学的结构体系才能建立,数学的进一步发展才有基础.
从泰勒斯开始,命题证明成为希腊数学的基本精神.
泰勒斯终身未婚,一生扑在研究哲学、数学、天文学.一次有人问他,你对自己的发现拿多少报酬?他答道:“当你把它告诉别人时,不说别人发现,而说是我发现,这就是对我最大的酬谢.”人们问他:“曾经见过的最稀奇的东西是什么?”他答道:“是寿命长的暴君.”
泰勒斯约活了77岁,人们纪念他的成就,在他坟墓雕像上,树碑立传歌颂这位距今已有2500多年的科学家:
“这位天文学家始祖之墓虽不甚宏伟,但在日月星辰的王国里,他顶天立地,万古流芳.”
泰勒斯观察天象时十分专心致志,哲学家柏拉图曾介绍过,有一次他只顾观察星空,不小心掉进了沟里,他的狼狈相引起人们的好笑,说:“他只想知道天上发生的事情,却看不见自己脚下的东西.”两千年后,哲学家黑格尔说了一句深刻的话:“只有那些永远躺在坑里,从不仰望高空的人,才不会掉进坑里.”
历史故事 1
历史故事2
早年泰勒斯曾一度很贫困,遭到人们的讥笑,说他研究数学无用,但他不气馁,一年冬天,他用天文知识预测到来年的橄榄必定大丰收,于是在头年的冬天租下了本地所有榨油机,由于没有竞争对手,又不是榨油季节,租金极低.来年橄榄果然大丰收,榨油机租金暴涨,他用高价租出去,从而赚了一大笔钱.
学派观点:
整个宇宙是自然的,是普通知识和理性的探讨所可以解释的.
大地是一个浮在水面上的扁平的盘子.
其学生阿那克西曼德说,天空是一 个完整的球体的一半,地球就处在球体的中心.
课堂小结
从泰勒斯开始,命题证明成为希腊数学的基本精神.
半圆上的圆周角是直角. ——泰勒斯定理
课堂习题
WZ//XY 吗? PQ//RS 吗?
直观经验的限制
WZ//XY 及 PQ//RS 是正确的
第二讲 古希腊数学
(公元前600—600)
知识回顾
古埃及的尼罗河每年泛滥,淹没田地,因此需要重新测量土地.
几何学「Geometry」一词包含土地(geo) 和测量(metry).
古希腊包括希腊半岛、爱琴海群岛和小亚细亚西安一带.希腊文明大约可以追溯到公元前2800年,一直延续到公元600年.公元前6世纪以后,由于经济和政治的进步,自然科学和数学得到高度发展.古希腊数学指公元前700年到公元600年.
古希腊
第一阶段:从公元前700年到前323年又称为古典时期或雅典时期.即从泰勒斯的伊奥尼亚学派到柏拉图学派为止;
第二阶段:是亚历山大时期,从公元前323年欧几里德起到公元前30年是全盛时期;
希腊数学发展的历史可分为三个阶段:
第三阶段:从公元前30年到公元600年,又称为亚历山大后期—衰弱时期,即罗马人统治下的时期.
柏拉图
亚历山大大帝
导入新课
希腊的数学内容包括算术(含代数)、几何学和三角学.
古希腊人学术辩论风气较浓,都有一批学者在一二位杰出人物的领导下活动,这类组织称为学派.这时期出现了泰勒斯学派(伊奥尼亚学派)、毕达哥拉斯学派等几个著名学派以及许多著名的数学家.
数学作为一门有组织、独立的和理性的学科来说,在古希腊学者登场之前是不存在的.
---M·克莱因
一、希腊数学的先行者
论证几何的发祥人——泰勒斯是伊奥尼亚学派的创始人,是现在所知的古希腊最早的数学家、哲学家,是希腊数学的先行者.
泰勒斯 (Thales, 公元前625 - 546)曾游学古埃及,他是将古埃及的几何知识引进希腊的人.
他试图将几何结果排成逻辑链条,排在前的可推导出排在后的,因而有了「证明」的念头.
泰勒斯生于伊奥尼亚的米利 都,出身奴隶主贵族家庭,政治地位显贵,生活富足.他本人可以做官出人头地,可他却把金钱、时间和精力都全部倾注于哲学与科学,被誉为“科学之父”和“希腊数学鼻祖”.
内容介绍
多说话并不表示有才智,
去找出一件唯一智慧的东西吧,
去选择一件唯一美好的东西吧,
这样就钳住许多饶舌汉的嘴.
他献身于科学,却招来非议,为此他写了一首诗回答这些人:
泰勒斯没有著作传世,了解他只能从后人的记载中.
泰勒斯还游访过巴比伦、埃及等古代文明国家,学到了那里的数学知识和天文学知识,晚年则转向哲学,他几乎涉猎了当时人类的全部思想和活动领域,被尊为“希腊七贤”之首.
论证数学
公元前6世纪,泰勒斯去埃及,第一个将埃及人的几何学带回希腊.据说他本人发现了许多几何命题,并创立了对几何命题的逻辑推理.泰勒斯发现了如下命题:
圆被任一直径平分.
等腰三角形的两底角相等.
3.两直线相交,对顶角相等.
4.在两个三角形中,有两角一夹边对应相等,则这两个三角形完全相等.
5.半圆周角是直角.
6.相似三角形的对应边成比例.
7.三角形内角和等于两直角.
泰勒斯曾利用天文学知识、预报了发生于公元585年的一次日食,并因此消弭了一场鏖战经年的战争.
天文、测量学家
另一项令人津津乐道的业绩是在埃及时,测定了金字塔的塔高.说明他已经熟悉相似三角形的基本性质.
泰勒斯在数学方面划时代的、影响最深远的贡献是引入命题证明的思想.它标志着人类对客观事物的认识已经从实践上升到理论.是数学史上一次不寻常的飞跃.
正是有了逻辑证明,数学命题的正确性得到了保证,数学理论才立于不败之地;数学定理之间的关系得到了揭示,数学的结构体系才能建立,数学的进一步发展才有基础.
从泰勒斯开始,命题证明成为希腊数学的基本精神.
泰勒斯终身未婚,一生扑在研究哲学、数学、天文学.一次有人问他,你对自己的发现拿多少报酬?他答道:“当你把它告诉别人时,不说别人发现,而说是我发现,这就是对我最大的酬谢.”人们问他:“曾经见过的最稀奇的东西是什么?”他答道:“是寿命长的暴君.”
泰勒斯约活了77岁,人们纪念他的成就,在他坟墓雕像上,树碑立传歌颂这位距今已有2500多年的科学家:
“这位天文学家始祖之墓虽不甚宏伟,但在日月星辰的王国里,他顶天立地,万古流芳.”
泰勒斯观察天象时十分专心致志,哲学家柏拉图曾介绍过,有一次他只顾观察星空,不小心掉进了沟里,他的狼狈相引起人们的好笑,说:“他只想知道天上发生的事情,却看不见自己脚下的东西.”两千年后,哲学家黑格尔说了一句深刻的话:“只有那些永远躺在坑里,从不仰望高空的人,才不会掉进坑里.”
历史故事 1
历史故事2
早年泰勒斯曾一度很贫困,遭到人们的讥笑,说他研究数学无用,但他不气馁,一年冬天,他用天文知识预测到来年的橄榄必定大丰收,于是在头年的冬天租下了本地所有榨油机,由于没有竞争对手,又不是榨油季节,租金极低.来年橄榄果然大丰收,榨油机租金暴涨,他用高价租出去,从而赚了一大笔钱.
学派观点:
整个宇宙是自然的,是普通知识和理性的探讨所可以解释的.
大地是一个浮在水面上的扁平的盘子.
其学生阿那克西曼德说,天空是一 个完整的球体的一半,地球就处在球体的中心.
课堂小结
从泰勒斯开始,命题证明成为希腊数学的基本精神.
半圆上的圆周角是直角. ——泰勒斯定理
课堂习题
WZ//XY 吗? PQ//RS 吗?
直观经验的限制
WZ//XY 及 PQ//RS 是正确的
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
