高中数学人教新课标A版选修3-1第二讲 古希腊数学 二 毕达哥拉斯学派(共34张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-1第二讲 古希腊数学 二 毕达哥拉斯学派(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
第二讲 古希腊数学
(公元前600—600)
知识回顾
泰勒斯把几何学作为一门演绎科学确立起来,是几何学的开端.
从泰勒斯开始,命题证明成为希腊数学的基本精神.
导入新课
伊奥尼亚学派之后,到了公元前6世纪末,由于波斯游牧民族的进攻,人们向西逃难,把希腊文化带到了西方.意大利和西西里岛变成了学术的新中心.毕达哥拉斯在这里创立了毕达哥拉斯学派.
古希腊
古埃及
古巴比伦
二、毕达哥拉斯学派
毕达哥拉斯(约公元前560—前480)出生在萨摩斯岛,在克罗托内(意大利半岛)组织了一个政治、科学、宗教三位一体的“友谊联盟”,盟里有300多名男女成员.这个团体组织严密,服从决定高于一切.需要保守的清规戒律很多,带有浓厚的宗教色彩.这就是毕达哥拉斯学派.
1.毕达哥拉斯
内容介绍
毕达哥拉斯学派创始人毕达哥拉斯是希腊论证数学的另一位祖师.毕达哥拉斯信奉“万物皆数”.他与我国的孔子处于同一时代.毕达哥拉斯没有著作传世,身世也充满谜团.
毕达哥拉斯
公元前551—前479年
精于哲学、数学、天文学、音乐理论
五十岁到意大利建立毕达哥拉斯学派
毕达哥拉斯曾师从伊奥尼亚学派的学者,以后游历埃及、巴比伦等地,接受古代流传下来的天文、数学知识,回家以后开始讲学.
毕达哥拉斯将信徒们分成两等.
一是普通听讲者,另一种是真正的学派成员,叫做μαθηματικο?
2.勾股定理与勾股数
勾股定理西方人叫毕达哥拉斯定理.
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,从朋友家的地板中发现了这个秘密.
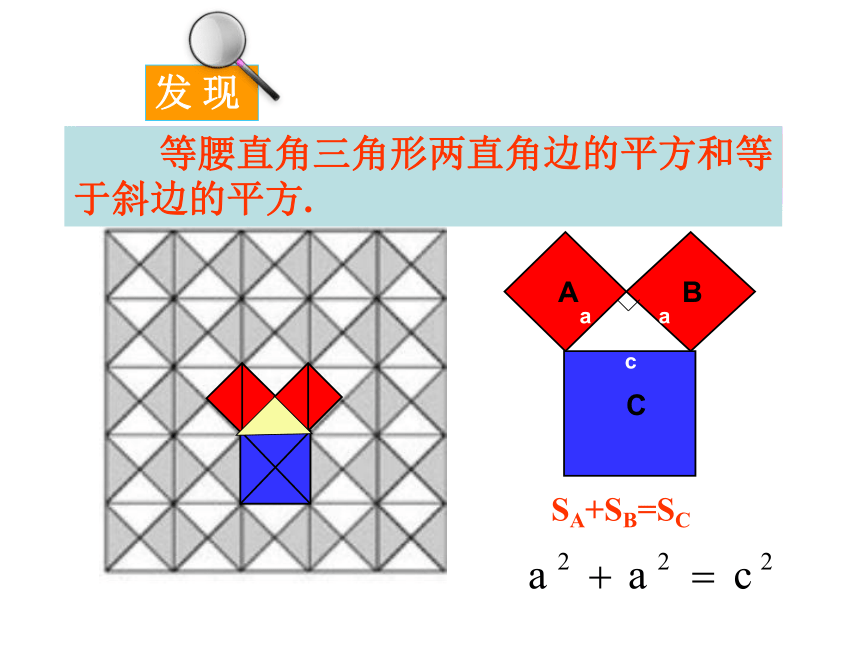
SA+SB=SC
1. 这块地板由哪些基本图形组成?
2.毕达哥拉斯在这块地板中发现了与三角形三边相邻的正方形面积有一种特殊的关系.你发现了吗?
3.从而毕达哥拉斯就得出了等腰直角三角形三边的某种数量关系.你觉得是什么关系?
发 现
等腰直角三角形两直角边的平方和等于斜边的平方.
这张邮票是希腊在一九五五年发行的.邮票上的图案是由三个棋盘排列而成的,它是对毕达哥拉斯定理的说明.
勾股定理可能是所有数学定理中证法最多的.卢米斯的《毕达哥拉斯命题》一书中记载有367种证法,实际的数目还不止这些.
毕达哥拉斯的证明方法现在已不可考.后人对它的证明只能进行一些合理的推测.
3.多边形数
毕达哥拉斯学派有一个基本信条——万物皆数.
费洛罗斯曾说:“人们所知道的任何事物都包含数.因此,如果没有数就既不可能表达,也不可能理解任何事物.”
毕达哥拉斯学派把自然数分为奇数、偶数、质数、合数、完全数、亲和数.至今二千多年来,一些数学家对质数(素数)、完全数、亲和数等仍在不停息地研究,成果丰盈,并且借助计算机和创新数学方法.
毕达哥拉斯学派认为10是一个完美的数.因为1,2,3,4是头四个自然数,分别代表水、火、气、土四种元素,而10=1+2+3+4被认为“包罗万象”了.最有趣的是把10作为宣誓的誓词,用崇敬的语言写道:
“创造诸神和人类的神圣的数啊,愿你赐福我们!啊!圣洁的‘4’啊,您孕育着永流不息的创造源泉!因为您起源于纯洁而深奥的‘1’,渐渐达到圣洁的4,然后生出圣洁的‘10’.它为天下之母,无所不包,无所不属,首出命世,永不偏齐,永不倦怠成为万物之钥”
多边形数也称“形数”,就是形与数的结合物.用点排成的图形.
图(1)中的点数叫做三角形数.第一个三角形数是1,第二个三角形数1+2=3,第三个三角形数是1+2+3=6……第n个三角形数是1+2+3……+n=
图(2)的点数叫做正方形数1,4,9,16,… 正方形数可以看作从1起连续奇数之和,如1+3+5+7+9+11=
正五边形数和正六边形数分别由序列:
后期毕达哥拉斯学派数学家尼可麦丘在《算术引论》中将多边形数推广到立体数.前四个三棱锥数为
1 1+3 1+3+6 1+3+6+10
毕达哥拉斯学派对数字的研究加强了数概念中的理论倾向,如果说埃及与巴比伦算术主要是实用的数字计算技巧,那么毕达哥拉斯学派的算术则更多体现出某种初等数论的萌芽,这是向理论数学过渡时观念上的飞跃.并且由于数形结合的观点,这种飞跃实质上推动了几何学的抽象化倾向.
万物皆数
4.不可公度
毕达哥拉斯学派相信,任何量都可以表示成两个整数之比.在几何上这相等于说:对于任意给定的两条线段,总能找到第三条线段,以它为单位线段能将给定的两条线段划分为整数段.希腊人称这样给定的两条线段为“可公度量”,意思是有公共的度量单位.
学派中有个勤学好问、爱动脑筋的青年,名叫希帕斯,他发现正方形边长为1时,它的对角线的长不是一个整数,也不是一个分数,而是一个新数就是我们后人所说的无理数 .
毕达哥拉斯学派后来却发现,并不是任意两条线段都是可公度的.
无理数的发现对毕达哥拉斯学派“万物皆数”的信条造成了强烈的震撼.后来人们又陆续发现了 以外的许多无理数.这就是数学史上的“第一次数学危机”.
希帕斯这一发现“违反”了教规,结果被投入大海葬身鱼腹.这是历史上震惊数学界的惨案.
第一次数学危机并没有轻易地很快解决,约从公元前的470到公元前370的一个世纪之后,才有柏拉图的学生欧多索斯初步解决了,他用纯粹公理化方法修改了量度和比例理论,微妙地处理与初步解决了可公度和不可公度.
课堂小结
几何学方面
1. 勾股定理与勾股数
2. 多边形,并类推到了立体几何(发现了正十二面体和正二十面体,并证明了多面体只限于这五种“宇宙体”.)
数的理论
万物皆数
形数(多边形数)
无理数(不可公度量)
课堂习题
1、 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个球,第2、3、4 堆最底层(第一层)分别按图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第 n 堆第 n 层就放一个乒乓球,以 f(n) 表示第 n?堆的乒乓球总数,则 f (3) =______, f (n) =__________ .
9
2 、 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和___________cm2.
49
第二讲 古希腊数学
(公元前600—600)
知识回顾
泰勒斯把几何学作为一门演绎科学确立起来,是几何学的开端.
从泰勒斯开始,命题证明成为希腊数学的基本精神.
导入新课
伊奥尼亚学派之后,到了公元前6世纪末,由于波斯游牧民族的进攻,人们向西逃难,把希腊文化带到了西方.意大利和西西里岛变成了学术的新中心.毕达哥拉斯在这里创立了毕达哥拉斯学派.
古希腊
古埃及
古巴比伦
二、毕达哥拉斯学派
毕达哥拉斯(约公元前560—前480)出生在萨摩斯岛,在克罗托内(意大利半岛)组织了一个政治、科学、宗教三位一体的“友谊联盟”,盟里有300多名男女成员.这个团体组织严密,服从决定高于一切.需要保守的清规戒律很多,带有浓厚的宗教色彩.这就是毕达哥拉斯学派.
1.毕达哥拉斯
内容介绍
毕达哥拉斯学派创始人毕达哥拉斯是希腊论证数学的另一位祖师.毕达哥拉斯信奉“万物皆数”.他与我国的孔子处于同一时代.毕达哥拉斯没有著作传世,身世也充满谜团.
毕达哥拉斯
公元前551—前479年
精于哲学、数学、天文学、音乐理论
五十岁到意大利建立毕达哥拉斯学派
毕达哥拉斯曾师从伊奥尼亚学派的学者,以后游历埃及、巴比伦等地,接受古代流传下来的天文、数学知识,回家以后开始讲学.
毕达哥拉斯将信徒们分成两等.
一是普通听讲者,另一种是真正的学派成员,叫做μαθηματικο?
2.勾股定理与勾股数
勾股定理西方人叫毕达哥拉斯定理.
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,从朋友家的地板中发现了这个秘密.
SA+SB=SC
1. 这块地板由哪些基本图形组成?
2.毕达哥拉斯在这块地板中发现了与三角形三边相邻的正方形面积有一种特殊的关系.你发现了吗?
3.从而毕达哥拉斯就得出了等腰直角三角形三边的某种数量关系.你觉得是什么关系?
发 现
等腰直角三角形两直角边的平方和等于斜边的平方.
这张邮票是希腊在一九五五年发行的.邮票上的图案是由三个棋盘排列而成的,它是对毕达哥拉斯定理的说明.
勾股定理可能是所有数学定理中证法最多的.卢米斯的《毕达哥拉斯命题》一书中记载有367种证法,实际的数目还不止这些.
毕达哥拉斯的证明方法现在已不可考.后人对它的证明只能进行一些合理的推测.
3.多边形数
毕达哥拉斯学派有一个基本信条——万物皆数.
费洛罗斯曾说:“人们所知道的任何事物都包含数.因此,如果没有数就既不可能表达,也不可能理解任何事物.”
毕达哥拉斯学派把自然数分为奇数、偶数、质数、合数、完全数、亲和数.至今二千多年来,一些数学家对质数(素数)、完全数、亲和数等仍在不停息地研究,成果丰盈,并且借助计算机和创新数学方法.
毕达哥拉斯学派认为10是一个完美的数.因为1,2,3,4是头四个自然数,分别代表水、火、气、土四种元素,而10=1+2+3+4被认为“包罗万象”了.最有趣的是把10作为宣誓的誓词,用崇敬的语言写道:
“创造诸神和人类的神圣的数啊,愿你赐福我们!啊!圣洁的‘4’啊,您孕育着永流不息的创造源泉!因为您起源于纯洁而深奥的‘1’,渐渐达到圣洁的4,然后生出圣洁的‘10’.它为天下之母,无所不包,无所不属,首出命世,永不偏齐,永不倦怠成为万物之钥”
多边形数也称“形数”,就是形与数的结合物.用点排成的图形.
图(1)中的点数叫做三角形数.第一个三角形数是1,第二个三角形数1+2=3,第三个三角形数是1+2+3=6……第n个三角形数是1+2+3……+n=
图(2)的点数叫做正方形数1,4,9,16,… 正方形数可以看作从1起连续奇数之和,如1+3+5+7+9+11=
正五边形数和正六边形数分别由序列:
后期毕达哥拉斯学派数学家尼可麦丘在《算术引论》中将多边形数推广到立体数.前四个三棱锥数为
1 1+3 1+3+6 1+3+6+10
毕达哥拉斯学派对数字的研究加强了数概念中的理论倾向,如果说埃及与巴比伦算术主要是实用的数字计算技巧,那么毕达哥拉斯学派的算术则更多体现出某种初等数论的萌芽,这是向理论数学过渡时观念上的飞跃.并且由于数形结合的观点,这种飞跃实质上推动了几何学的抽象化倾向.
万物皆数
4.不可公度
毕达哥拉斯学派相信,任何量都可以表示成两个整数之比.在几何上这相等于说:对于任意给定的两条线段,总能找到第三条线段,以它为单位线段能将给定的两条线段划分为整数段.希腊人称这样给定的两条线段为“可公度量”,意思是有公共的度量单位.
学派中有个勤学好问、爱动脑筋的青年,名叫希帕斯,他发现正方形边长为1时,它的对角线的长不是一个整数,也不是一个分数,而是一个新数就是我们后人所说的无理数 .
毕达哥拉斯学派后来却发现,并不是任意两条线段都是可公度的.
无理数的发现对毕达哥拉斯学派“万物皆数”的信条造成了强烈的震撼.后来人们又陆续发现了 以外的许多无理数.这就是数学史上的“第一次数学危机”.
希帕斯这一发现“违反”了教规,结果被投入大海葬身鱼腹.这是历史上震惊数学界的惨案.
第一次数学危机并没有轻易地很快解决,约从公元前的470到公元前370的一个世纪之后,才有柏拉图的学生欧多索斯初步解决了,他用纯粹公理化方法修改了量度和比例理论,微妙地处理与初步解决了可公度和不可公度.
课堂小结
几何学方面
1. 勾股定理与勾股数
2. 多边形,并类推到了立体几何(发现了正十二面体和正二十面体,并证明了多面体只限于这五种“宇宙体”.)
数的理论
万物皆数
形数(多边形数)
无理数(不可公度量)
课堂习题
1、 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个球,第2、3、4 堆最底层(第一层)分别按图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第 n 堆第 n 层就放一个乒乓球,以 f(n) 表示第 n?堆的乒乓球总数,则 f (3) =______, f (n) =__________ .
9
2 、 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和___________cm2.
49
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
