苏科九年级数学下册5.2二次函数的图象和性质第二课时课件(共16张PPT)
文档属性
| 名称 | 苏科九年级数学下册5.2二次函数的图象和性质第二课时课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 886.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 06:45:47 | ||
图片预览

文档简介
(共16张PPT)
初中数学九年级下册
(苏科版)
5.2二次函数图象和性质(2)
向上
向下
(0 ,0)
(0 ,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
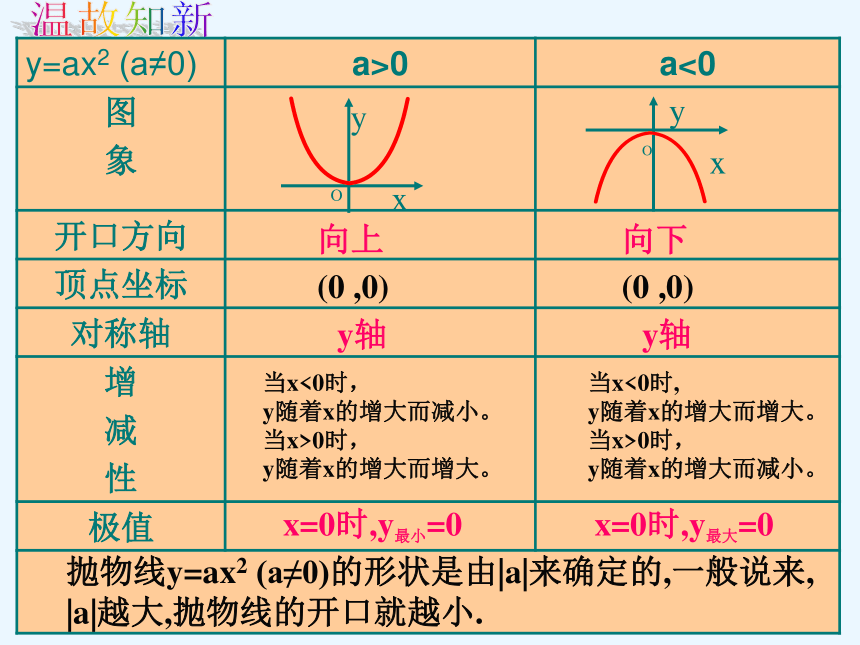
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小.
y=ax2 (a≠0) a>0 a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
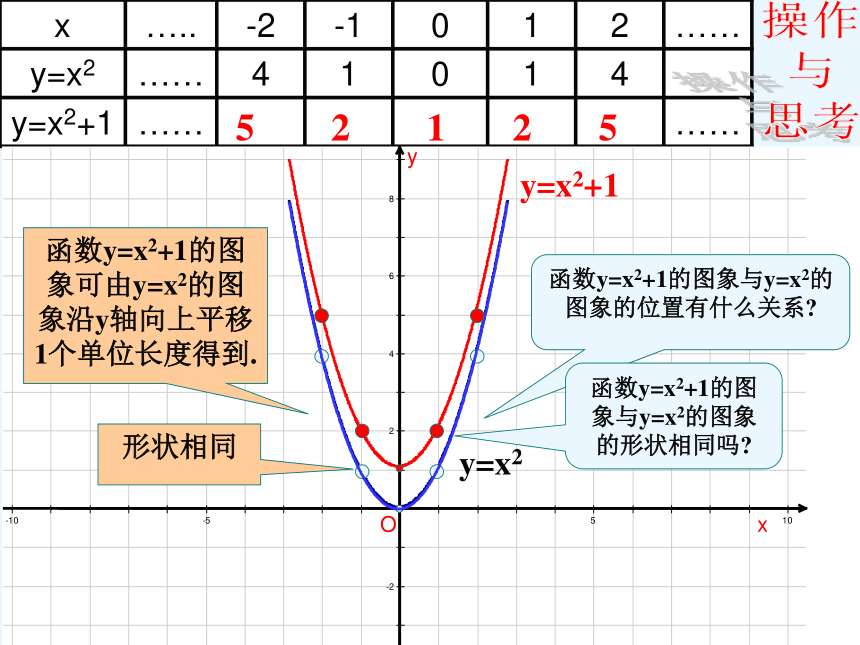
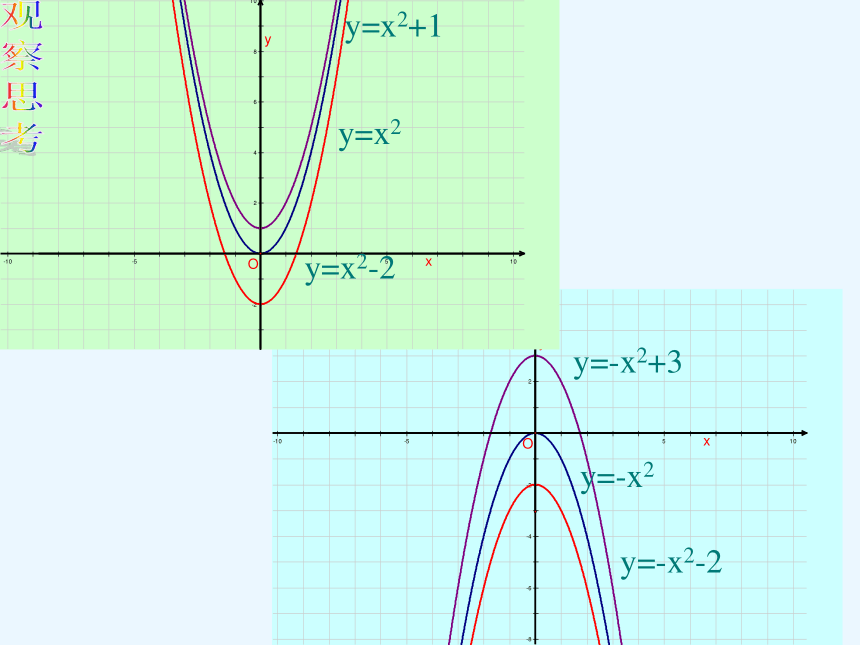
y=x2
y=x2+1
函数y=x2+1的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
函数y=x2+1的图象与y=x2的图象的形状相同吗?
形状相同
5 2 1 2 5
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2+1 …… ……
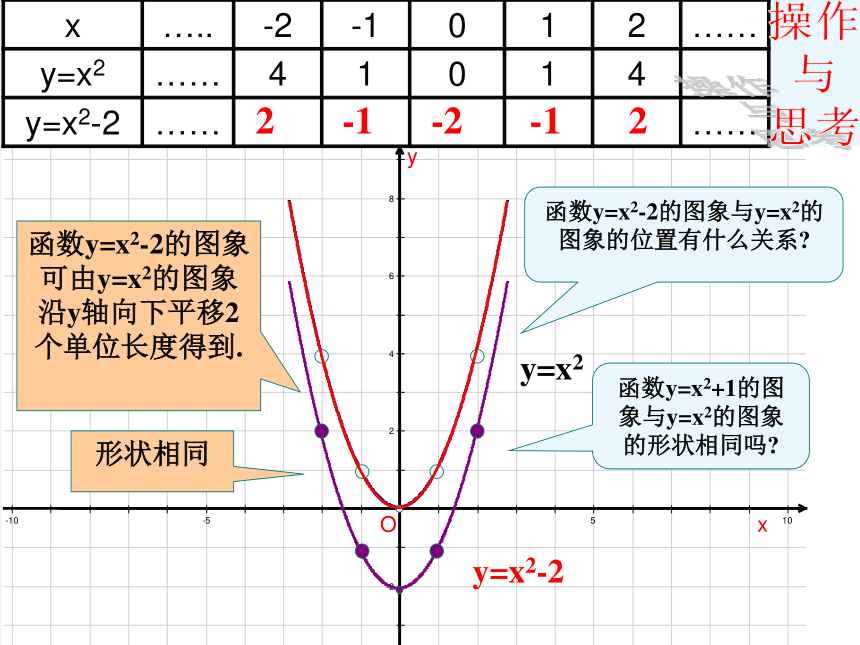
y=x2
y=x2-2
2 -1 -2 -1 2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象与y=x2的图象的形状相同吗?
形状相同
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2-2 …… ……
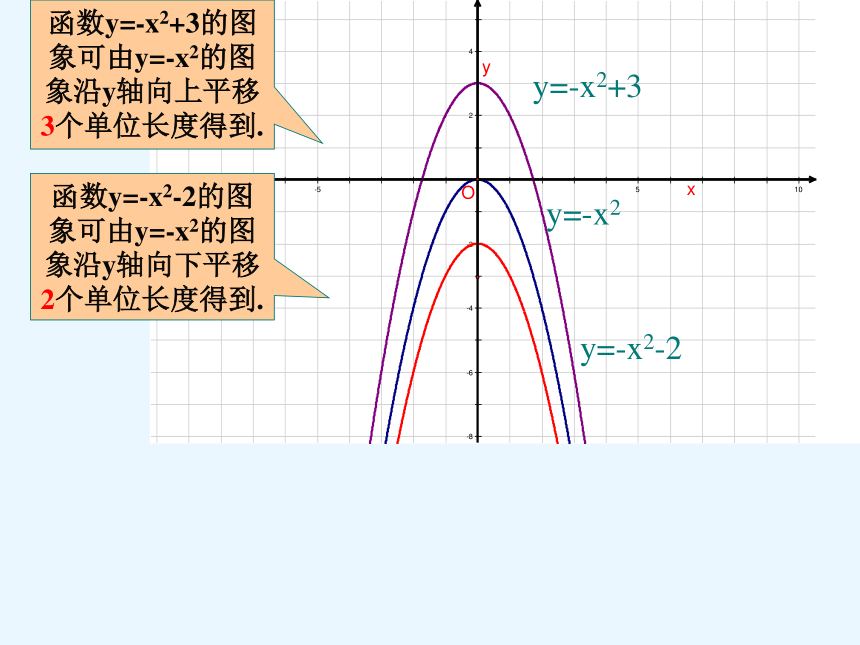
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
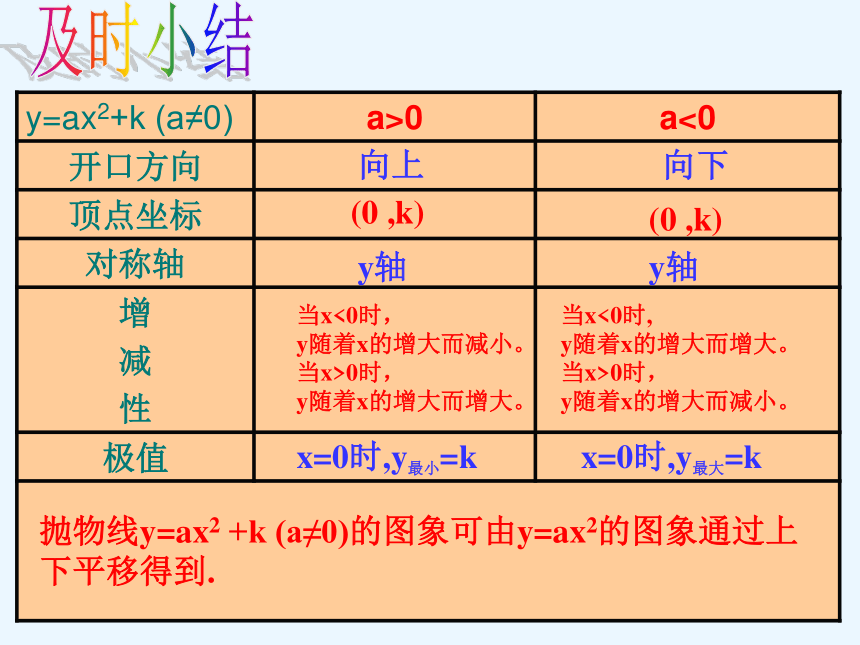
向上
向下
(0 ,k)
(0 ,k)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=k
x=0时,y最大=k
抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移得到.
y=ax2+k (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
(1)抛物线y=-3x2+5的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
(3)二次函数y=ax2+k (a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+k的表达式为 。若点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐标为 点D的坐标为 .
(2)抛物线y=7x2-3的开口 ,对称轴是 ,顶点坐标是 ,当x 时,y随x的增大而 ,当x 时,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
y=2x2-3
(-2,5)
或
(4)二次函数y=mx2+m-2的图像的顶点在y轴的负半轴上,且开口向上,则m的取值范围为( )
A.m>2 B.m<2 C.0 (1)函数y=4x2+5的图象可由y=4x2的图象
向 平移 个单位得到;y=4x2-11的图象
可由 y=4x2的图象向 平移 个单位得到。
(3)将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是 。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是 。
(2)将函数y=-3x2+4的图象向 平移 个单位可得
y=-3x2的图象;将y=2x2-7的图象向 平移 个
单位得到y=2x2的图象。将y=x2-7的图象
向 平移 个单位可得到 y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
(1)已知二次函数y=3x2+4,点A(x1,y1), B(x2,y2),
C(x3,y3), D(x4,y4)在其图象上,且x2< x4<0,
0|x1|, |x3|>|x4|, 则 ( )
x1
x2
x3
x4
y1
y4
y3
y2
A.y1>y2>y3>y4
B.y2>y1>y3>y4
C.y3>y2>y4>y1
D.y4>y2>y3>y1
B
(2)已知二次函数y=ax2+k,当x取x1,x2(x1≠x2,
x1,x2分别是A,B两点的横坐标)时,函数值相等,
则当x取x1+x2时,函数值为 ( )
A. a+k B. a-k C. –k D. k
D
(3) 函数y=ax2-a与y=
在同一直角坐标系中的图象可能是 ( )
A
(4) 一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
1.二次函数y=x2+k的图象是什么?
答:是抛物线
2.二次函数的性质有哪些?请填写下表:
向上
Y轴
(0,0)
最小值是0
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
向上
Y轴
(0,k)
最小值是k
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,k)
最大值是k
Y随x的增大而增大
Y随x的增大而减小
函数 开口方向 对称轴 顶 点坐 标 Y的最值 增减性
在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
初中数学九年级下册
(苏科版)
5.2二次函数图象和性质(2)
向上
向下
(0 ,0)
(0 ,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小.
y=ax2 (a≠0) a>0 a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
y=x2
y=x2+1
函数y=x2+1的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
函数y=x2+1的图象与y=x2的图象的形状相同吗?
形状相同
5 2 1 2 5
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2+1 …… ……
y=x2
y=x2-2
2 -1 -2 -1 2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象与y=x2的图象的形状相同吗?
形状相同
x ….. -2 -1 0 1 2 ……
y=x2 …… 4 1 0 1 4
y=x2-2 …… ……
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
向上
向下
(0 ,k)
(0 ,k)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=k
x=0时,y最大=k
抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移得到.
y=ax2+k (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
(1)抛物线y=-3x2+5的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
(3)二次函数y=ax2+k (a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+k的表达式为 。若点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐标为 点D的坐标为 .
(2)抛物线y=7x2-3的开口 ,对称轴是 ,顶点坐标是 ,当x 时,y随x的增大而 ,当x 时,y随x的增大而 ,
当x= 时,取得最 值,这个值等于 。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
y=2x2-3
(-2,5)
或
(4)二次函数y=mx2+m-2的图像的顶点在y轴的负半轴上,且开口向上,则m的取值范围为( )
A.m>2 B.m<2 C.0
向 平移 个单位得到;y=4x2-11的图象
可由 y=4x2的图象向 平移 个单位得到。
(3)将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是 。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是 。
(2)将函数y=-3x2+4的图象向 平移 个单位可得
y=-3x2的图象;将y=2x2-7的图象向 平移 个
单位得到y=2x2的图象。将y=x2-7的图象
向 平移 个单位可得到 y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
(1)已知二次函数y=3x2+4,点A(x1,y1), B(x2,y2),
C(x3,y3), D(x4,y4)在其图象上,且x2< x4<0,
0
x1
x2
x3
x4
y1
y4
y3
y2
A.y1>y2>y3>y4
B.y2>y1>y3>y4
C.y3>y2>y4>y1
D.y4>y2>y3>y1
B
(2)已知二次函数y=ax2+k,当x取x1,x2(x1≠x2,
x1,x2分别是A,B两点的横坐标)时,函数值相等,
则当x取x1+x2时,函数值为 ( )
A. a+k B. a-k C. –k D. k
D
(3) 函数y=ax2-a与y=
在同一直角坐标系中的图象可能是 ( )
A
(4) 一位篮球运动员跳起投篮,球沿抛物线
运行,然后准确落入蓝筐内,已知蓝筐的中心离地面的
距离为3.05m。
1、球在空中运行的最大高度是多少米?
2、如果运动员跳投时,球出手离地面的高度 为2.25m ,
则他离篮筐中心的水平距离AB是多少?
1.二次函数y=x2+k的图象是什么?
答:是抛物线
2.二次函数的性质有哪些?请填写下表:
向上
Y轴
(0,0)
最小值是0
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
向上
Y轴
(0,k)
最小值是k
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,k)
最大值是k
Y随x的增大而增大
Y随x的增大而减小
函数 开口方向 对称轴 顶 点坐 标 Y的最值 增减性
在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
