北师大版 六年级下册 比例的认识(共20张PPT)
文档属性
| 名称 | 北师大版 六年级下册 比例的认识(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 22:38:31 | ||
图片预览



文档简介
(共20张PPT)
2.1 比例的认识
二 比例
学习目标
结合“图片像不像”“调制蜂蜜水”等情境,找到相等的比,理解比例的意义,认识比例的各部分名称,能通过化简比和求比值等方法判断两个比能否组成比例。
通过观察、计算,发现并理解比例的基本性质,能判断两个比能否组成比例。
经历观察比较、自主探究等活动,提高分析能力和概括能力。
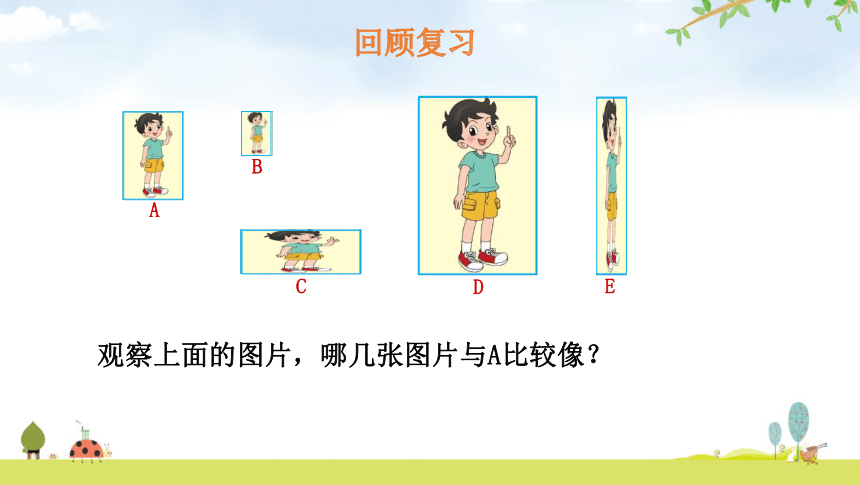
A
B
C
D
E
观察上面的图片,哪几张图片与A比较像?
回顾复习
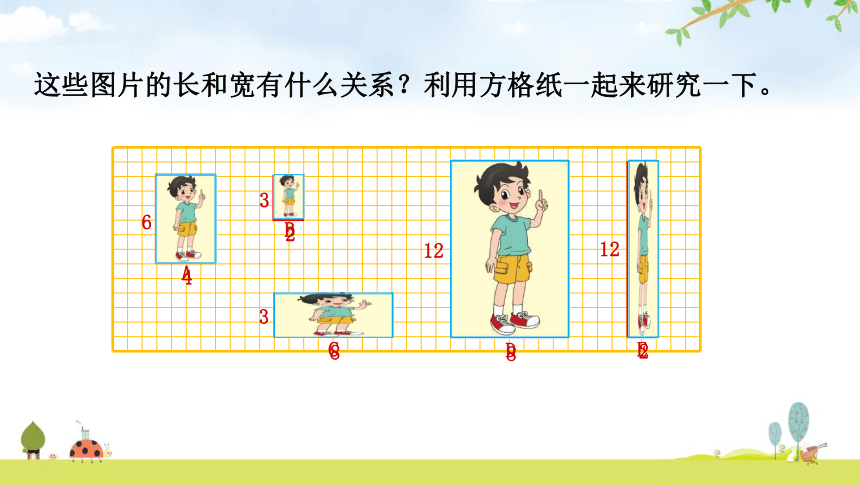
A
B
C
D
E
6
4
3
2
3
8
12
8
12
2
A
B
C
D
E
这些图片的长和宽有什么关系?利用方格纸一起来研究一下。
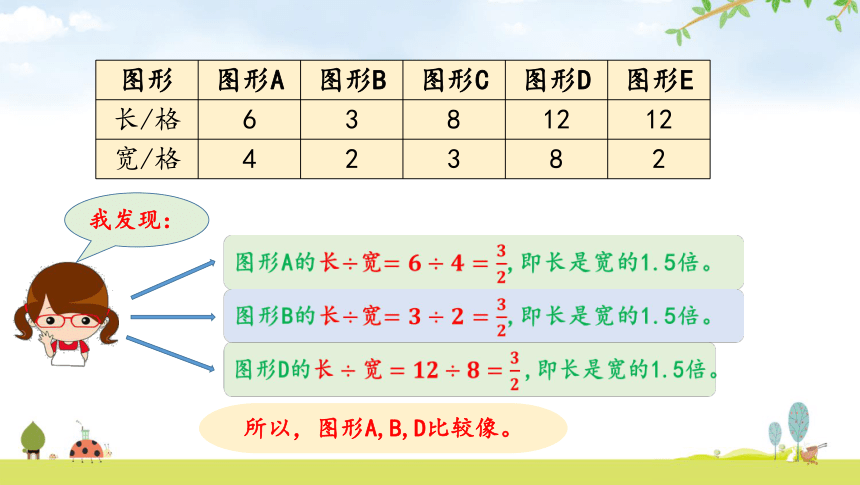
我发现:
图形D的长宽,即长是宽的1.5倍。
图形A的长宽,即长是宽的1.5倍。
图形B的长宽,即长是宽的1.5倍。
所以,图形A,B,D比较像。
图形 图形A 图形B 图形C 图形D 图形E
长/格 6 3 8 12 12
宽/格 4 2 3 8 2
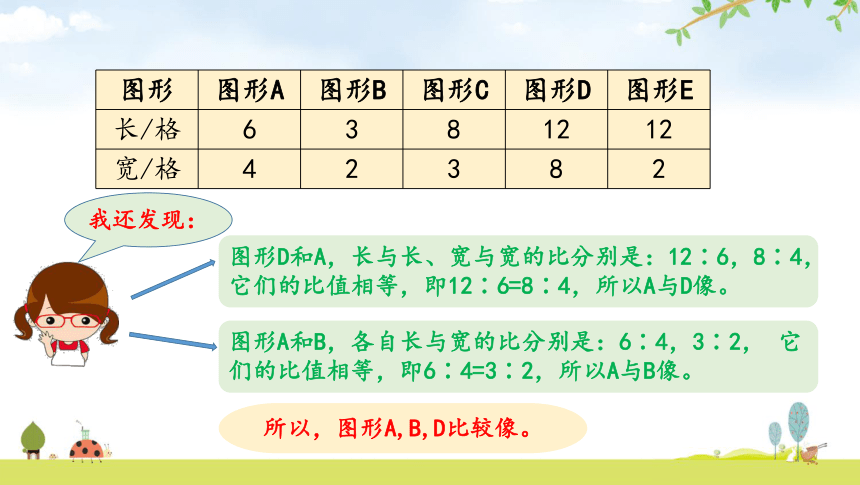
图形 图形A 图形B 图形C 图形D 图形E
长/格 6 3 8 12 12
宽/格 4 2 3 8 2
我还发现:
图形D和A,长与长、宽与宽的比分别是:12∶6,8∶4, 它们的比值相等,即12∶6=8∶4,所以A与D像。
所以,图形A,B,D比较像。
图形A和B,各自长与宽的比分别是:6∶4,3∶2, 它们的比值相等,即6∶4=3∶2,所以A与B像。
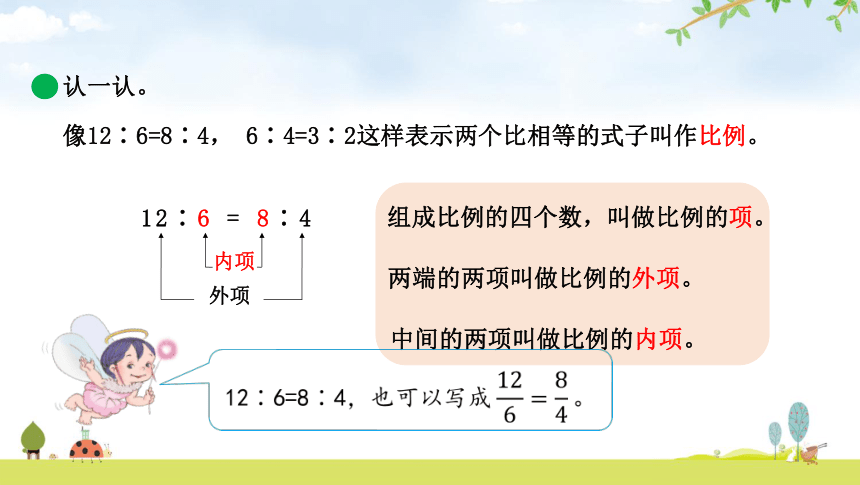
认一认。
像12∶6=8∶4, 6∶4=3∶2这样表示两个比相等的式子叫作比例。
内项
12∶6 = 8∶4
外项
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
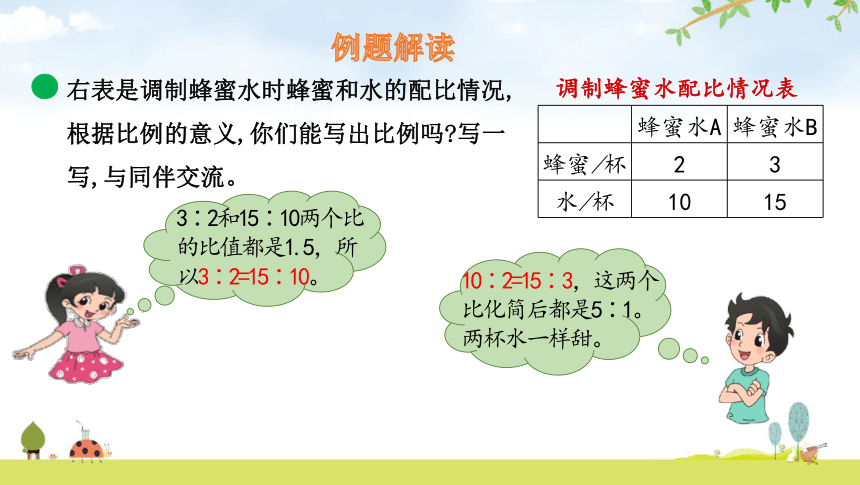
例题解读
调制蜂蜜水配比情况表
蜂蜜水A 蜂蜜水B
蜂蜜/杯 2 3
水/杯 10 15
右表是调制蜂蜜水时蜂蜜和水的配比情况,根据比例的意义,你们能写出比例吗?写一写,与同伴交流。
3∶2和15∶10两个比的比值都是1.5,所以3∶2=15∶10。
10∶2=15∶3,这两个比化简后都是5∶1。两杯水一样甜。
12×4=6×8
6×2=4×3
3×10=2×15
10×3=2×15
写出上节课学习的几个比例,仔细观察,你会有新的发现。
淘气的发现你同意吗?再写几个比例验证一下。
12∶6=8∶4
内项的积:6×8=48
外项的积:12×4=48
3∶2=15∶10
内项的积:2×15=30
外项的积:3×10=30
发 现
15∶12=10∶8
内项的积:12×10=120
外项的积:15×8=120
1.5∶0.5=3∶1
内项的积:0.5×3=1.5
外项的积:1.5×1=1.5
验 证
真是这样!
例如:12∶6和8∶4
12×4=48
6×8=48
两个外项的乘积=两个内项的乘积
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
用字母表示比例的基本性质:
=
或
ad= bc
a:b=c:d(b、d≠0)
小 结
比例的相关概念
组成比例的四个数叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
表示两个比相等的式子叫做比例。
内项
12∶6 = 8∶4
外项
比例的基本性质
=
或
ad= bc
a:b=c:d(b、d≠0)
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
1.⑴分别写出图中两个长方形长与长的
比和宽与宽的比,判断这两个比能否
组成比例。
长与长的比=3∶9 宽与宽的比=2∶6。
3∶9=2∶6 能组成比例
第1个长方形:长与宽的比=3∶2;
第2个长方形:长与宽的比=6∶9。
3∶2=9∶6 能组成比例
⑵分别写出图中每个长方形长与宽的
比,判断这两个能否组成比例。
随堂小测
2. 下面哪组中的两个比可以组成比例?把能组成的比例写出来。
(1)6∶10和9∶15
(2)20∶5和1∶4
6∶10=0.6
9∶15=0.6
所以, 6∶10=9∶15可以组成比例。
20∶5=4
1∶4=0.25
所以, 20∶5和1∶4不能组成比例。
规范解答:
3. 下列各比中哪些能组成比例,请写出来。
0.6∶0.8
3∶1.2
0.5∶0.2
0.6∶0.8=
3∶1.2=0.5∶0.2
规范解答:
计算比值:
0.6∶0.8=3∶4
3∶1.2=5∶2
0.5∶0.2=5∶2
=10∶9
=10∶3
=3∶4
规范解答:
4. 用图中的4个数据可以组成多少个比例?
3∶1.5=4 ∶ 2
3∶4=1.5∶2
2∶1.5=4 ∶ 3
2∶ 4=1.5∶3
1.5∶3=2∶ 4
1.5∶2=3∶4
4∶3=2∶1.5
4∶2=3∶1.5
5. 判断2、4、8、16这四个数能否组成比例?
规范解答:
根据比例的意义判断。
根据比例的基本性质判断。
所以2、4、8、16这四个数能组成比例。
因为
因为
所以
所以
方法一
方法二
易错提醒
判断:8∶2=4是比例。 ( )
错误解答
正确解答
√
×
判断: 8∶2=4是比例。 ( )
错因分析:在比例中,等号的两侧必须都是比。
8∶2=4∶1是比例。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
2.1 比例的认识
二 比例
学习目标
结合“图片像不像”“调制蜂蜜水”等情境,找到相等的比,理解比例的意义,认识比例的各部分名称,能通过化简比和求比值等方法判断两个比能否组成比例。
通过观察、计算,发现并理解比例的基本性质,能判断两个比能否组成比例。
经历观察比较、自主探究等活动,提高分析能力和概括能力。
A
B
C
D
E
观察上面的图片,哪几张图片与A比较像?
回顾复习
A
B
C
D
E
6
4
3
2
3
8
12
8
12
2
A
B
C
D
E
这些图片的长和宽有什么关系?利用方格纸一起来研究一下。
我发现:
图形D的长宽,即长是宽的1.5倍。
图形A的长宽,即长是宽的1.5倍。
图形B的长宽,即长是宽的1.5倍。
所以,图形A,B,D比较像。
图形 图形A 图形B 图形C 图形D 图形E
长/格 6 3 8 12 12
宽/格 4 2 3 8 2
图形 图形A 图形B 图形C 图形D 图形E
长/格 6 3 8 12 12
宽/格 4 2 3 8 2
我还发现:
图形D和A,长与长、宽与宽的比分别是:12∶6,8∶4, 它们的比值相等,即12∶6=8∶4,所以A与D像。
所以,图形A,B,D比较像。
图形A和B,各自长与宽的比分别是:6∶4,3∶2, 它们的比值相等,即6∶4=3∶2,所以A与B像。
认一认。
像12∶6=8∶4, 6∶4=3∶2这样表示两个比相等的式子叫作比例。
内项
12∶6 = 8∶4
外项
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
例题解读
调制蜂蜜水配比情况表
蜂蜜水A 蜂蜜水B
蜂蜜/杯 2 3
水/杯 10 15
右表是调制蜂蜜水时蜂蜜和水的配比情况,根据比例的意义,你们能写出比例吗?写一写,与同伴交流。
3∶2和15∶10两个比的比值都是1.5,所以3∶2=15∶10。
10∶2=15∶3,这两个比化简后都是5∶1。两杯水一样甜。
12×4=6×8
6×2=4×3
3×10=2×15
10×3=2×15
写出上节课学习的几个比例,仔细观察,你会有新的发现。
淘气的发现你同意吗?再写几个比例验证一下。
12∶6=8∶4
内项的积:6×8=48
外项的积:12×4=48
3∶2=15∶10
内项的积:2×15=30
外项的积:3×10=30
发 现
15∶12=10∶8
内项的积:12×10=120
外项的积:15×8=120
1.5∶0.5=3∶1
内项的积:0.5×3=1.5
外项的积:1.5×1=1.5
验 证
真是这样!
例如:12∶6和8∶4
12×4=48
6×8=48
两个外项的乘积=两个内项的乘积
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
用字母表示比例的基本性质:
=
或
ad= bc
a:b=c:d(b、d≠0)
小 结
比例的相关概念
组成比例的四个数叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
表示两个比相等的式子叫做比例。
内项
12∶6 = 8∶4
外项
比例的基本性质
=
或
ad= bc
a:b=c:d(b、d≠0)
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
1.⑴分别写出图中两个长方形长与长的
比和宽与宽的比,判断这两个比能否
组成比例。
长与长的比=3∶9 宽与宽的比=2∶6。
3∶9=2∶6 能组成比例
第1个长方形:长与宽的比=3∶2;
第2个长方形:长与宽的比=6∶9。
3∶2=9∶6 能组成比例
⑵分别写出图中每个长方形长与宽的
比,判断这两个能否组成比例。
随堂小测
2. 下面哪组中的两个比可以组成比例?把能组成的比例写出来。
(1)6∶10和9∶15
(2)20∶5和1∶4
6∶10=0.6
9∶15=0.6
所以, 6∶10=9∶15可以组成比例。
20∶5=4
1∶4=0.25
所以, 20∶5和1∶4不能组成比例。
规范解答:
3. 下列各比中哪些能组成比例,请写出来。
0.6∶0.8
3∶1.2
0.5∶0.2
0.6∶0.8=
3∶1.2=0.5∶0.2
规范解答:
计算比值:
0.6∶0.8=3∶4
3∶1.2=5∶2
0.5∶0.2=5∶2
=10∶9
=10∶3
=3∶4
规范解答:
4. 用图中的4个数据可以组成多少个比例?
3∶1.5=4 ∶ 2
3∶4=1.5∶2
2∶1.5=4 ∶ 3
2∶ 4=1.5∶3
1.5∶3=2∶ 4
1.5∶2=3∶4
4∶3=2∶1.5
4∶2=3∶1.5
5. 判断2、4、8、16这四个数能否组成比例?
规范解答:
根据比例的意义判断。
根据比例的基本性质判断。
所以2、4、8、16这四个数能组成比例。
因为
因为
所以
所以
方法一
方法二
易错提醒
判断:8∶2=4是比例。 ( )
错误解答
正确解答
√
×
判断: 8∶2=4是比例。 ( )
错因分析:在比例中,等号的两侧必须都是比。
8∶2=4∶1是比例。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
