北师大版数学六年级下册2第2节 比例的应用(课件共19张PPT)
文档属性
| 名称 | 北师大版数学六年级下册2第2节 比例的应用(课件共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 23:23:24 | ||
图片预览






文档简介
(共19张PPT)
2.2 比例的应用
二 比例
学习目标
经历用多种方法解决“物物交换”问题的过程,体会解决问题方法的多样化,理解解比例的意义。
在解决问题的过程中列出含有未知数的比例,并自主探索解比例的方法,能够根据“两个内项的积等于两个外项的积”求比例中的未知项,会正确解比例。
培养认真书写和准确计算的学习习惯。
回顾复习
你能求出比例中缺少的项是多少吗?
( )6=210
1.8 ( )=1.55
利用比例的基本性质:
ad=bc
1.2
6
例题解读
解题之前学习新知识。
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,求比例中的未知项,叫做解比例。
14个玩具汽车可以换多少本小人书?写出你的想法。
4个
4个
4个
2个
5本
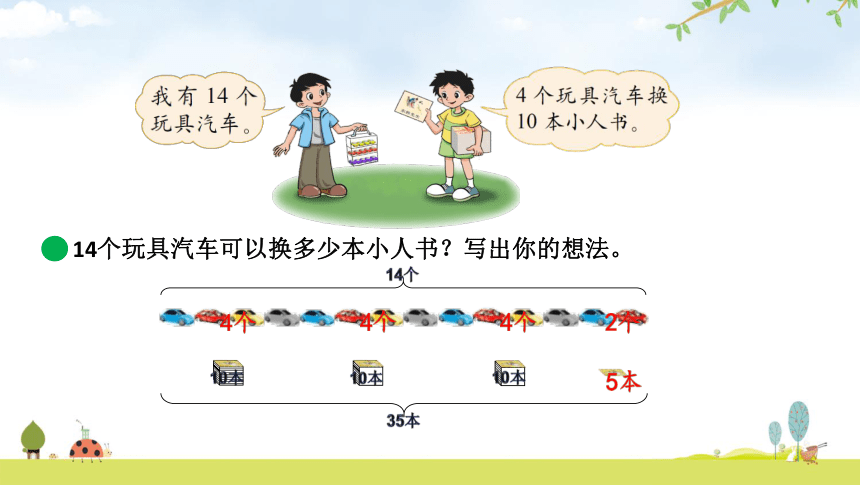
14个玩具汽车可以换多少本小人书?写出你的想法。
4个
10本
4个
10本
4个
10本
2个
5本
35本
14个玩具汽车可以换多少本小人书?写出你的想法。
14÷4=3.5
3.5×10=35(本)
假设14个玩具汽车可以换本小人书,尝试用比例的方法解决问题。
4∶10=14∶
一辆小汽车换几本小人书
解:4 =140
=35
答:14个玩具汽车可以换35本书。
根据内项的积等于外项的积
假设14个玩具汽车可以换本小人书,尝试用比例的方法解决问题。
14∶4= ∶10
玩具汽车与小人书间的倍数
解:4 =140
=35
答:14个玩具汽车可以换35本书。
根据内项的积等于外项的积
24∶0.3 = x∶0.4
解下面的比例,与同伴交流。
解:0.3 =9.6
=32
解:7 =14
=2
检验:
24∶0.3=80
30∶0.4=80
检验:
24∶0.3= 30∶0.4
把求出的结果代入比例验算一下,看等式是否成立。
小 结
解比例
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,求比例中的未知项,叫做解比例。
(1)根据比例的基本性质,把比例转化成
外项和内项积相等的形式(即方程)。
(2)解方程求未知数。
解比例的计算步骤
随堂小测
1.作业本上的6个小星星可以换2面小红旗。
淘气的作业本上已经有了15个小星星。
⑴15个小星星可以换多少面小红旗?写出你的想法。
6个
2面
15个
6个
6个
3个
2面
2面
1面
5面
1.作业本上的6个小星星可以换2面小红旗。
淘气的作业本上已经有了15个小星星。
⑵假设15个小星星可以换面小红旗,你能列比例并解决问题吗?
6∶2=15∶x
解: 6x=30
x=5
答:15个小星星可以换5面小红旗。
(1)∶10∶
解:
2. 解方程。
=10×
1.2 =0.8
12 =2.4×3
12 =7.2
=0.6
(2)0.4∶ ∶2
(3)
解:
解:
=
=
=
1.2=0.4×2
规范解答:
3. 餐馆给餐具消毒,要用100ml消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入水多少毫升?
100∶=1∶150
已知消毒液有100 ,如果设加入水为,
则可以列出比例式
消毒液∶水=1∶150
规范解答:
3. 餐馆给餐具消毒,要用100ml消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入水多少毫升?
100∶=1∶150
解:设应加入水为
答:应加入水15000
消毒液∶水=1∶150
x=100×150
x=15000
4.广州塔高600m,是目前世界第一高的电视塔。
星星公司设计制作了这座电视塔的模型,模
型的高度与实际高度的比是1:300。模型的高
度是多少米?
解:设模型的高度是 m。
1∶300=∶600
=2
答:模型的高度是2米。
规范解答:
规范解答:
5. 中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
∶10=1.5∶0.5
解:设它的高度为
答:它的高度为30
0.5x=10×1.5
x=30
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
2.2 比例的应用
二 比例
学习目标
经历用多种方法解决“物物交换”问题的过程,体会解决问题方法的多样化,理解解比例的意义。
在解决问题的过程中列出含有未知数的比例,并自主探索解比例的方法,能够根据“两个内项的积等于两个外项的积”求比例中的未知项,会正确解比例。
培养认真书写和准确计算的学习习惯。
回顾复习
你能求出比例中缺少的项是多少吗?
( )6=210
1.8 ( )=1.55
利用比例的基本性质:
ad=bc
1.2
6
例题解读
解题之前学习新知识。
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,求比例中的未知项,叫做解比例。
14个玩具汽车可以换多少本小人书?写出你的想法。
4个
4个
4个
2个
5本
14个玩具汽车可以换多少本小人书?写出你的想法。
4个
10本
4个
10本
4个
10本
2个
5本
35本
14个玩具汽车可以换多少本小人书?写出你的想法。
14÷4=3.5
3.5×10=35(本)
假设14个玩具汽车可以换本小人书,尝试用比例的方法解决问题。
4∶10=14∶
一辆小汽车换几本小人书
解:4 =140
=35
答:14个玩具汽车可以换35本书。
根据内项的积等于外项的积
假设14个玩具汽车可以换本小人书,尝试用比例的方法解决问题。
14∶4= ∶10
玩具汽车与小人书间的倍数
解:4 =140
=35
答:14个玩具汽车可以换35本书。
根据内项的积等于外项的积
24∶0.3 = x∶0.4
解下面的比例,与同伴交流。
解:0.3 =9.6
=32
解:7 =14
=2
检验:
24∶0.3=80
30∶0.4=80
检验:
24∶0.3= 30∶0.4
把求出的结果代入比例验算一下,看等式是否成立。
小 结
解比例
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,求比例中的未知项,叫做解比例。
(1)根据比例的基本性质,把比例转化成
外项和内项积相等的形式(即方程)。
(2)解方程求未知数。
解比例的计算步骤
随堂小测
1.作业本上的6个小星星可以换2面小红旗。
淘气的作业本上已经有了15个小星星。
⑴15个小星星可以换多少面小红旗?写出你的想法。
6个
2面
15个
6个
6个
3个
2面
2面
1面
5面
1.作业本上的6个小星星可以换2面小红旗。
淘气的作业本上已经有了15个小星星。
⑵假设15个小星星可以换面小红旗,你能列比例并解决问题吗?
6∶2=15∶x
解: 6x=30
x=5
答:15个小星星可以换5面小红旗。
(1)∶10∶
解:
2. 解方程。
=10×
1.2 =0.8
12 =2.4×3
12 =7.2
=0.6
(2)0.4∶ ∶2
(3)
解:
解:
=
=
=
1.2=0.4×2
规范解答:
3. 餐馆给餐具消毒,要用100ml消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入水多少毫升?
100∶=1∶150
已知消毒液有100 ,如果设加入水为,
则可以列出比例式
消毒液∶水=1∶150
规范解答:
3. 餐馆给餐具消毒,要用100ml消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入水多少毫升?
100∶=1∶150
解:设应加入水为
答:应加入水15000
消毒液∶水=1∶150
x=100×150
x=15000
4.广州塔高600m,是目前世界第一高的电视塔。
星星公司设计制作了这座电视塔的模型,模
型的高度与实际高度的比是1:300。模型的高
度是多少米?
解:设模型的高度是 m。
1∶300=∶600
=2
答:模型的高度是2米。
规范解答:
规范解答:
5. 中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
∶10=1.5∶0.5
解:设它的高度为
答:它的高度为30
0.5x=10×1.5
x=30
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
