小学数学北师大版六年级下册4 第2节 正比例(共20张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下册4 第2节 正比例(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 23:49:03 | ||
图片预览





文档简介
(共20张PPT)
4.2 正比例
四 正比例与反比例
学习目标
结合“正方形的周长与边长,正方形的面积与边长‘路程、时间与速度”等情境,经历正比例意义的构建过程,能从变化中看到“不变”,认识正比例。
能根据正比例的意义,判断两个相关联的量是不是成正比例。
能列举生活中成正比例的实例,感受正比例在生活中的广泛应用。
回顾复习
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
例题解读
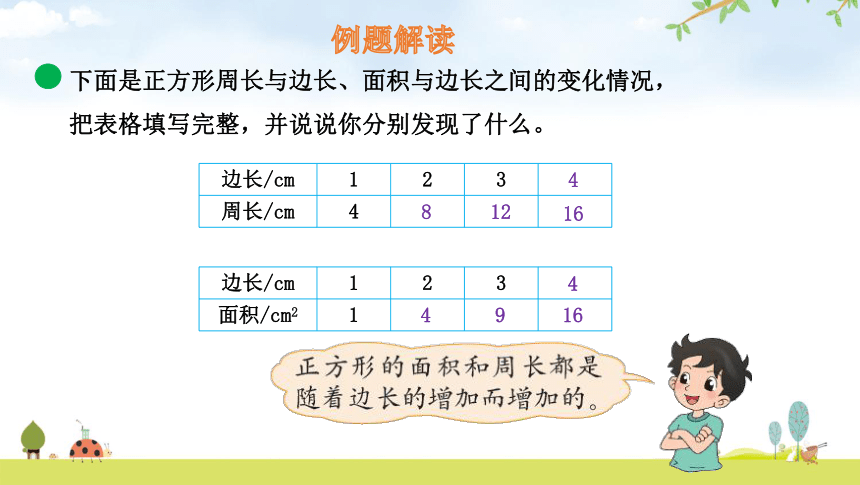
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
8
12
4
16
4
9
4
16
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
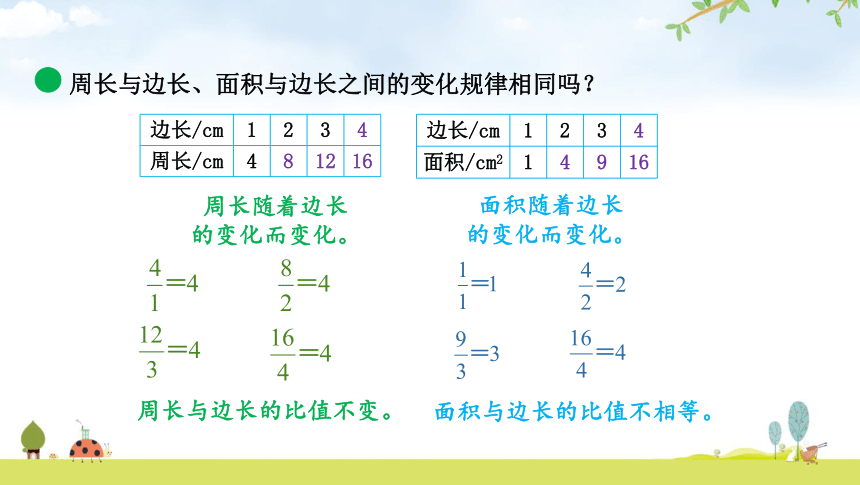
周长与边长的比值不变。
面积与边长的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
周长与边长、面积与边长之间的变化规律相同吗?
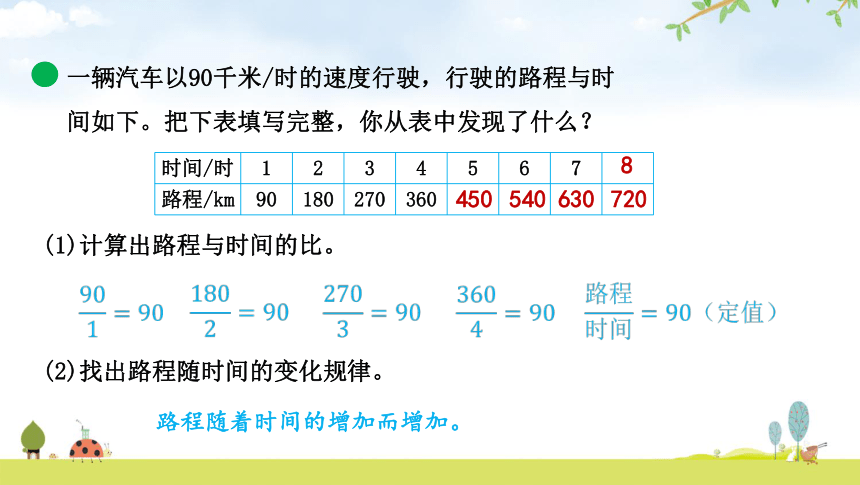
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
(1)计算出路程与时间的比。
(2)找出路程随时间的变化规律。
路程随着时间的增加而增加。
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
路程与时间的比值是一定的。
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
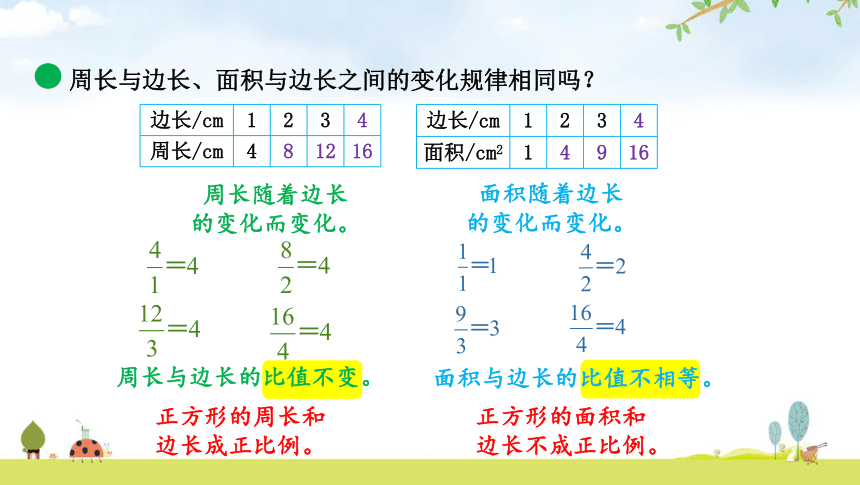
周长与边长的比值不变。
面积与边长的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
周长与边长、面积与边长之间的变化规律相同吗?
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
圆的面积与半径成正比例吗?
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
圆的面积随着半径的变化而变化,我想是成正比例的。
圆的面积公式
圆的面积 3.14 12.56 28.26
半径 1 2 3
我列个表试一试。
比值不相等……
乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
乐乐的年龄与爸爸年龄的比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
所以,他们的年龄不成正比例。
34
35
36
37
分别举一个成正比例和一个不成正比例的例子,
与同伴交流。
成正比例:
圆的周长与圆的直径。
不成正比例:
一个人的身高与他的年龄。
小 结
正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。它们的关系叫做正比例关系。
用字母表示就是:
判断两个量是不是成正比例
(1)确定这两个量是否为相关联的量。
(2)如果这两个相关联的量中向对应
的两个数的比值(也就是商)一
定,这两个量就成正比例关系;
否则,就不成正比例关系。
随堂小测
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
1.
把表填完整,你从中发现了什么?
2.4
3.2
4
4.8
5.6
6.4
成正比例
应付金额与所买邮票的数量成正比例吗?
80∶1=80
规范解答:
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对的时间的比,并比较比值的大小。
160∶2=80
320∶4=80
240∶3=80
400∶5=80
480∶6=80
路程与相对的时间的比的比值都相等。
=
=
=
=
=
=
80
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
规范解答:
(2)说一说这个比值表示什么。
这个比值表示这辆汽车的行驶速度。
规范解答:
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例;
因为路程和时间对应的比值一定,都等于80。
每支圆珠笔的价钱一定
规范解答:
3. 小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔, 要用多少钱?
用比例法解答
解:小刚要用元钱。
4 =6×3
=4.5
答:小刚要用4.5元钱。
规范解答:
用比例法解答
2.4 =1.5×4
=2.5
4. 小兰的身高1.5m,她的影长是2.4m,如果同一时间、
同一地点测得一棵树的影子长4m,这棵树有多高?
解:设这棵树高m。
答:这棵树高2.5m。
同一时间、同一地点,
身高和影长成正比例关系
易错提醒
判断:因为,所以和成正比例关系。 ( )
错误解答
正确解答
√
×
判断:因为,所以和成正比例关系。 ( )
错因分析:因为在中,没有强调的值是一定的。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4.2 正比例
四 正比例与反比例
学习目标
结合“正方形的周长与边长,正方形的面积与边长‘路程、时间与速度”等情境,经历正比例意义的构建过程,能从变化中看到“不变”,认识正比例。
能根据正比例的意义,判断两个相关联的量是不是成正比例。
能列举生活中成正比例的实例,感受正比例在生活中的广泛应用。
回顾复习
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
例题解读
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
8
12
4
16
4
9
4
16
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
周长与边长的比值不变。
面积与边长的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
周长与边长、面积与边长之间的变化规律相同吗?
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
(1)计算出路程与时间的比。
(2)找出路程随时间的变化规律。
路程随着时间的增加而增加。
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
路程与时间的比值是一定的。
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
周长与边长的比值不变。
面积与边长的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
周长与边长、面积与边长之间的变化规律相同吗?
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
圆的面积与半径成正比例吗?
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
圆的面积随着半径的变化而变化,我想是成正比例的。
圆的面积公式
圆的面积 3.14 12.56 28.26
半径 1 2 3
我列个表试一试。
比值不相等……
乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
乐乐的年龄与爸爸年龄的比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
所以,他们的年龄不成正比例。
34
35
36
37
分别举一个成正比例和一个不成正比例的例子,
与同伴交流。
成正比例:
圆的周长与圆的直径。
不成正比例:
一个人的身高与他的年龄。
小 结
正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。它们的关系叫做正比例关系。
用字母表示就是:
判断两个量是不是成正比例
(1)确定这两个量是否为相关联的量。
(2)如果这两个相关联的量中向对应
的两个数的比值(也就是商)一
定,这两个量就成正比例关系;
否则,就不成正比例关系。
随堂小测
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
1.
把表填完整,你从中发现了什么?
2.4
3.2
4
4.8
5.6
6.4
成正比例
应付金额与所买邮票的数量成正比例吗?
80∶1=80
规范解答:
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对的时间的比,并比较比值的大小。
160∶2=80
320∶4=80
240∶3=80
400∶5=80
480∶6=80
路程与相对的时间的比的比值都相等。
=
=
=
=
=
=
80
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
规范解答:
(2)说一说这个比值表示什么。
这个比值表示这辆汽车的行驶速度。
规范解答:
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例;
因为路程和时间对应的比值一定,都等于80。
每支圆珠笔的价钱一定
规范解答:
3. 小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔, 要用多少钱?
用比例法解答
解:小刚要用元钱。
4 =6×3
=4.5
答:小刚要用4.5元钱。
规范解答:
用比例法解答
2.4 =1.5×4
=2.5
4. 小兰的身高1.5m,她的影长是2.4m,如果同一时间、
同一地点测得一棵树的影子长4m,这棵树有多高?
解:设这棵树高m。
答:这棵树高2.5m。
同一时间、同一地点,
身高和影长成正比例关系
易错提醒
判断:因为,所以和成正比例关系。 ( )
错误解答
正确解答
√
×
判断:因为,所以和成正比例关系。 ( )
错因分析:因为在中,没有强调的值是一定的。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
