第2节 圆柱的表面积(共22张PPT)
图片预览




文档简介
(共22张PPT)
1.2 圆柱的表面积
一 圆柱与圆锥
学习目标
通过想象、操作等活动,理解圆柱表面积的意义及圆柱的侧面展开图与圆柱的关系,体会转化思想。
探究并掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积,并能解决生活中的实际问题。
在解决问题的过程中体会数学与生活的密切联系。
1. 圆柱有( )个底面,它们是( );
有( )侧面,是( ),有( )条高,
这些高都( )。
2. 圆柱的侧面展开是( ),长方形的长等于
( ),宽等于( )。
2
大小相等的圆
1
曲面
无数
长度相等
长方形
底面周长
高
回顾复习
3.折一折,想一想,能得到什么图形?写在( )里。
长方体
正方体
圆柱
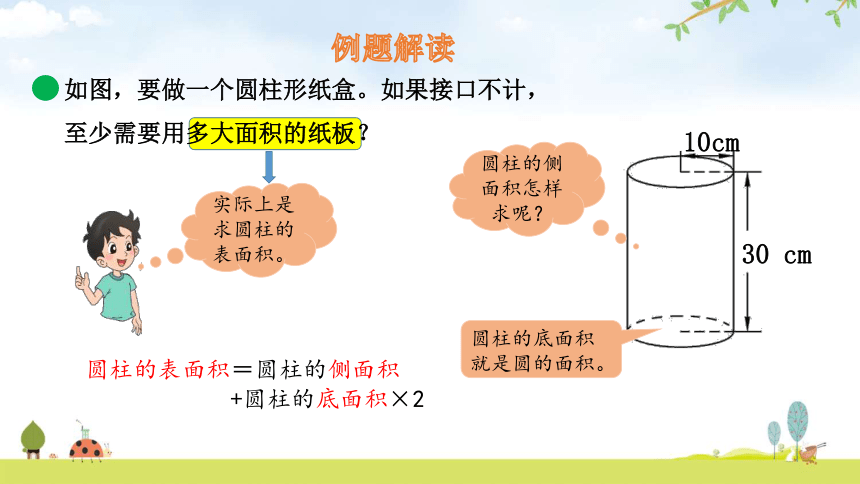
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
例题解读
30 cm
10cm
实际上是求圆柱的表面积。
圆柱的侧面积怎样求呢?
圆柱的底面积就是圆的面积。
圆柱的表面积=圆柱的侧面积
+圆柱的底面积×2
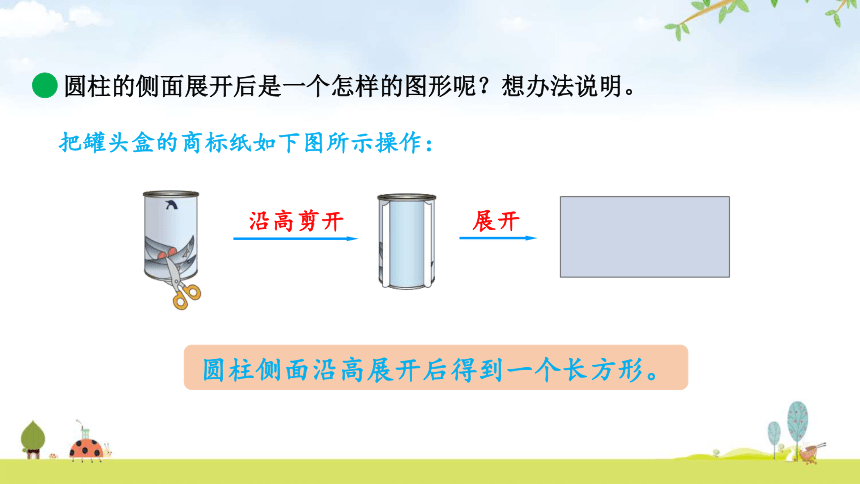
圆柱的侧面展开后是一个怎样的图形呢?想办法说明。
把罐头盒的商标纸如下图所示操作:
沿高剪开
展开
圆柱侧面沿高展开后得到一个长方形。
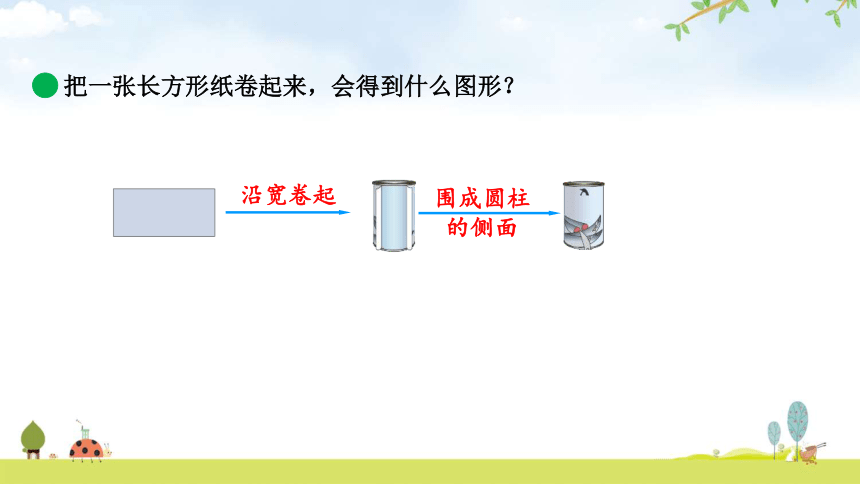
把一张长方形纸卷起来,会得到什么图形?
沿宽卷起
围成圆柱的侧面
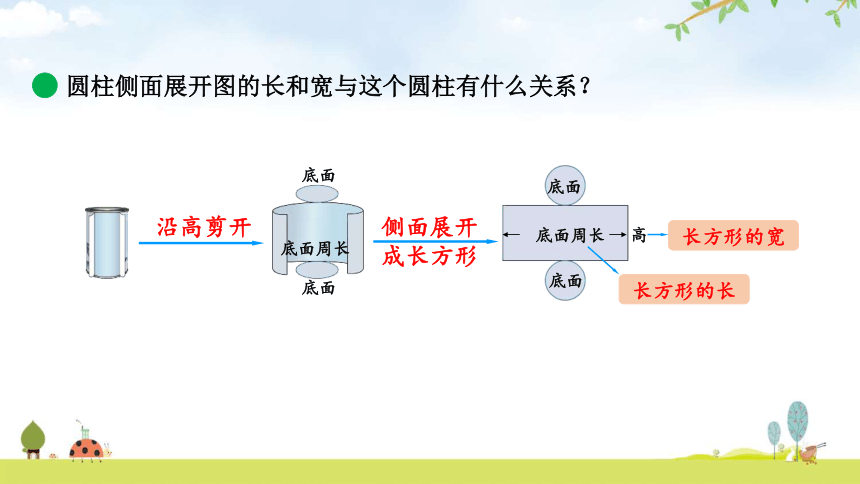
圆柱侧面展开图的长和宽与这个圆柱有什么关系?
底面
底面
高
底面周长
沿高剪开
长方形的长
底面
底面
底面周长
长方形的宽
侧面展开成长方形
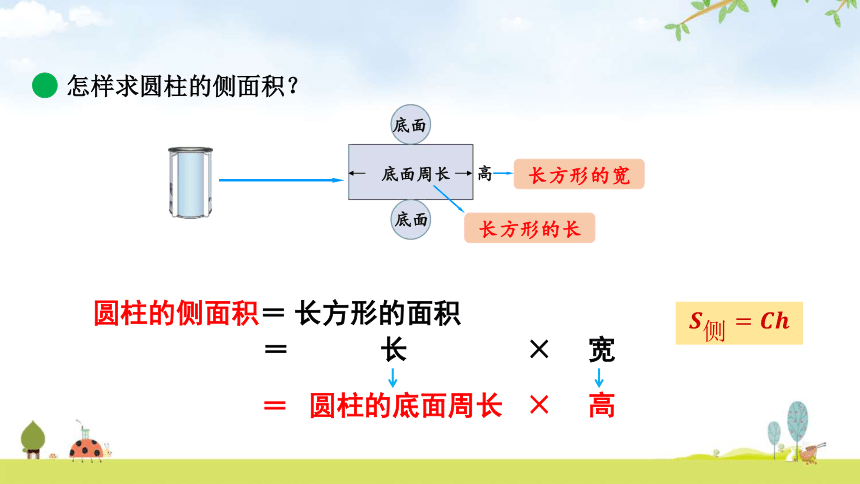
怎样求圆柱的侧面积?
底面
底面
高
底面周长
长方形的长
长方形的宽
圆柱的侧面积= 长方形的面积
= 长 × 宽
=
圆柱的底面周长
× 高
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
30 cm
10cm
10 cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4 dm
5 dm
答:至少需要75.36平方分米的铁皮。
要算哪几个面呢?
水桶没有盖哦!
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
?cm
答:这个薯片盒的侧面积是188.4平方厘米,
表面积是244.92平方厘米。
小 结
圆柱的侧面展开图及圆柱的表面积
沿高剪开
展开
底面
底面
高
底面的周长
展开
长方形的长
底面
底面
底面的周长
长方形的宽
圆柱的侧面积
=
圆柱的底面周长
× 高
圆柱的表面积=圆柱的侧面积+圆柱的底面积×2
圆柱的表面积计算公式
圆柱表面积的特殊情况
随堂小测
1.一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是 5 cm,高是 20 cm。这张商标纸展开后是一个长方形,它的长和宽各是多少厘米?
长=圆柱底面周长
2×5×3.14
=10×3.14
=31.4(cm)
宽=圆柱的高
20 cm
2.连一连,并在括号中填出相应的数。
( )
( )
( )
( )
21.98cm
4cm
9.42cm
8cm
3.求圆柱的表面积。
3.14×4×6+3.14×(4÷2)2×2=100.48(cm2)
3.14×(3×2)×10+3.14×32×2=244.92(dm2)
4. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
就是求帽子的表面积
(注意:只有1个底面哦)
规范解答:
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)2=314(cm2 )
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200 cm2的面料。
5.如果把一段圆柱形的木头截成两截,它的表面积会有什么变化呢?
变化多少呢?(木头的底面半径是0.3 m,长是2 m)
规范解答:
表面积增加了,
增加的是截面处两个圆面的面积。
答:表面积会增加,增加 0.5652 。
易错提醒
判断:把圆柱的侧面沿一条线剪开后,得到的一定是长方形或正方形。( )
错误解答
正确解答
√
×
判断:把圆柱的侧面沿一条线剪开后,得到的一定是长方形或正方形。( )
错因分析:当圆柱的侧面不是沿高剪开时,展开后
得到的图形可能是平行四边形。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1.2 圆柱的表面积
一 圆柱与圆锥
学习目标
通过想象、操作等活动,理解圆柱表面积的意义及圆柱的侧面展开图与圆柱的关系,体会转化思想。
探究并掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积,并能解决生活中的实际问题。
在解决问题的过程中体会数学与生活的密切联系。
1. 圆柱有( )个底面,它们是( );
有( )侧面,是( ),有( )条高,
这些高都( )。
2. 圆柱的侧面展开是( ),长方形的长等于
( ),宽等于( )。
2
大小相等的圆
1
曲面
无数
长度相等
长方形
底面周长
高
回顾复习
3.折一折,想一想,能得到什么图形?写在( )里。
长方体
正方体
圆柱
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
例题解读
30 cm
10cm
实际上是求圆柱的表面积。
圆柱的侧面积怎样求呢?
圆柱的底面积就是圆的面积。
圆柱的表面积=圆柱的侧面积
+圆柱的底面积×2
圆柱的侧面展开后是一个怎样的图形呢?想办法说明。
把罐头盒的商标纸如下图所示操作:
沿高剪开
展开
圆柱侧面沿高展开后得到一个长方形。
把一张长方形纸卷起来,会得到什么图形?
沿宽卷起
围成圆柱的侧面
圆柱侧面展开图的长和宽与这个圆柱有什么关系?
底面
底面
高
底面周长
沿高剪开
长方形的长
底面
底面
底面周长
长方形的宽
侧面展开成长方形
怎样求圆柱的侧面积?
底面
底面
高
底面周长
长方形的长
长方形的宽
圆柱的侧面积= 长方形的面积
= 长 × 宽
=
圆柱的底面周长
× 高
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
30 cm
10cm
10 cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4 dm
5 dm
答:至少需要75.36平方分米的铁皮。
要算哪几个面呢?
水桶没有盖哦!
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
?cm
答:这个薯片盒的侧面积是188.4平方厘米,
表面积是244.92平方厘米。
小 结
圆柱的侧面展开图及圆柱的表面积
沿高剪开
展开
底面
底面
高
底面的周长
展开
长方形的长
底面
底面
底面的周长
长方形的宽
圆柱的侧面积
=
圆柱的底面周长
× 高
圆柱的表面积=圆柱的侧面积+圆柱的底面积×2
圆柱的表面积计算公式
圆柱表面积的特殊情况
随堂小测
1.一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是 5 cm,高是 20 cm。这张商标纸展开后是一个长方形,它的长和宽各是多少厘米?
长=圆柱底面周长
2×5×3.14
=10×3.14
=31.4(cm)
宽=圆柱的高
20 cm
2.连一连,并在括号中填出相应的数。
( )
( )
( )
( )
21.98cm
4cm
9.42cm
8cm
3.求圆柱的表面积。
3.14×4×6+3.14×(4÷2)2×2=100.48(cm2)
3.14×(3×2)×10+3.14×32×2=244.92(dm2)
4. 一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
就是求帽子的表面积
(注意:只有1个底面哦)
规范解答:
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)2=314(cm2 )
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200 cm2的面料。
5.如果把一段圆柱形的木头截成两截,它的表面积会有什么变化呢?
变化多少呢?(木头的底面半径是0.3 m,长是2 m)
规范解答:
表面积增加了,
增加的是截面处两个圆面的面积。
答:表面积会增加,增加 0.5652 。
易错提醒
判断:把圆柱的侧面沿一条线剪开后,得到的一定是长方形或正方形。( )
错误解答
正确解答
√
×
判断:把圆柱的侧面沿一条线剪开后,得到的一定是长方形或正方形。( )
错因分析:当圆柱的侧面不是沿高剪开时,展开后
得到的图形可能是平行四边形。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
