第3节 圆柱的体积(共22张PPT)
图片预览








文档简介
(共22张PPT)
1.3 圆柱的体积
一 圆柱与圆锥
学习目标
通过具体情境观察,实物感知等活动,感受物体体积的大小,发展空间观念。
通过圆柱与长方体的“类比”,经历探索圆柱体积计算方法的过程,体会类比思想和转化思想。
掌握圆柱体积的计算方法,能正确计算圆柱的体积,并能运用圆柱体积的计算方法解决简单的实际问题。
正方体的体积
=底面积高
=棱长棱长棱长
长方体的体积
=底面积高
=长宽高
回顾复习
圆的面积 = (已知圆的半径r)
= (已知圆的直径d)
= (已知圆的周长C)
张老师准备给孩子买一个蛋糕,到了蛋糕店他发现有两款蛋糕比较不错,而且价格相同。这时他犹豫了,买哪款蛋糕更划算呢?你能帮他选一选吗?
情景导入
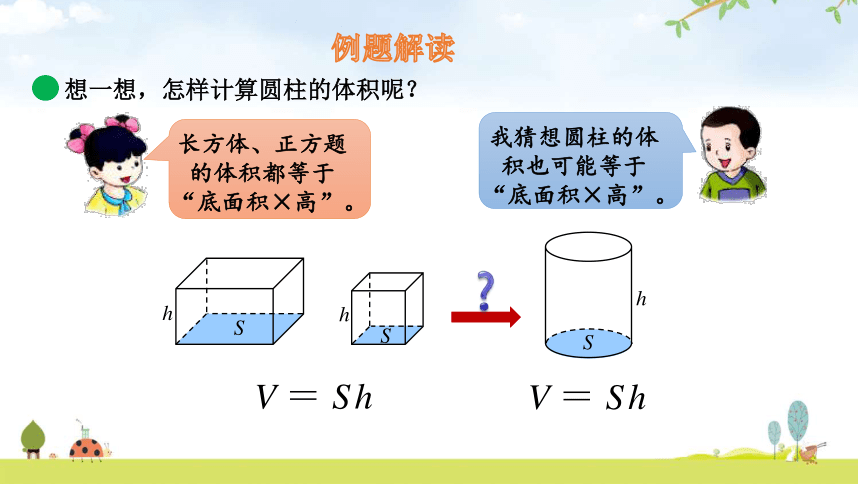
想一想,怎样计算圆柱的体积呢?
例题解读
长方体、正方题的体积都等于“底面积×高”。
我猜想圆柱的体积也可能等于“底面积×高”。
尝试验证你的猜想,并与同伴交流。
从叠硬币来看,用“底面积×高”能计算出圆柱的体积。
圆柱底面周长的一半
圆柱的高
底面
半径
拼成的长方体与圆来的圆柱有什么关系?
沿着高把圆柱切开再拼起来
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
圆柱体积计算公式是:
这个长方体的底面积等于圆柱的____________,高等于圆柱的____。
高
底面圆的面积
体积相等
笑笑了解到一根柱子的底面半径0.4 m,高为5 m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
3.14×0.42×5
=0.5024×5
=2.512(m3)
柱子的体积:
尝试解决下面的问题。
杯子的容积:
3.14×(6÷2)2×16
=28.26×16
=452.16(cm3)
452.16 cm3=452.16 mL
笑笑了解到一根柱子的底面半径0.4 m,高为5 m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
尝试解决下面的问题。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
底面半径:
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm3)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512cm3。
规范解答:
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
答:这根金箍棒重19.8448千克。
规范解答:
7.9×2512=19844.8(g)
19844.8g=19.8448kg
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
体积:
12.56×200=2512(cm3)
小 结
推导圆柱体积的计算公式
圆柱体积的计算公式
1.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
随堂小测
2. 一根圆柱形木料,底面积为 75 ,长 90 cm。
它的体积是多少?
答:它的体积是6750 cm3 。
规范解答:
圆柱的体积=圆柱底面积高
=7590
=6750()
圆柱的体积=底面积高
保温杯的容积:
50.24×15
=753.6 (cm?)
=0.7536(L)
所以带这杯水不够喝。
3. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量
底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,
带这杯水够喝吗?
保温杯的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2)
规范解答:
0.75361
4. 下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
10 cm
8 cm
杯子的容积:
50.24×10
=502.4 (cm3 )
=502.4 (mL)
杯子的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2 )
规范解答:
502.4498
答:所以杯子能装下这袋牛奶。
易错提醒
判断:圆柱的高不变,底面直径扩大到原来的4倍,体积也扩大到
原来的4倍。 ( )
错误解答
正确解答
√
×
错因分析:圆柱的高不变,底面半径、直径或者周长扩大到
原来的倍,则体积扩大到原来的倍。
判断:圆柱的高不变,底面直径扩大到原来的4倍,体积也扩大到
原来的4倍。 ( )
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1.3 圆柱的体积
一 圆柱与圆锥
学习目标
通过具体情境观察,实物感知等活动,感受物体体积的大小,发展空间观念。
通过圆柱与长方体的“类比”,经历探索圆柱体积计算方法的过程,体会类比思想和转化思想。
掌握圆柱体积的计算方法,能正确计算圆柱的体积,并能运用圆柱体积的计算方法解决简单的实际问题。
正方体的体积
=底面积高
=棱长棱长棱长
长方体的体积
=底面积高
=长宽高
回顾复习
圆的面积 = (已知圆的半径r)
= (已知圆的直径d)
= (已知圆的周长C)
张老师准备给孩子买一个蛋糕,到了蛋糕店他发现有两款蛋糕比较不错,而且价格相同。这时他犹豫了,买哪款蛋糕更划算呢?你能帮他选一选吗?
情景导入
想一想,怎样计算圆柱的体积呢?
例题解读
长方体、正方题的体积都等于“底面积×高”。
我猜想圆柱的体积也可能等于“底面积×高”。
尝试验证你的猜想,并与同伴交流。
从叠硬币来看,用“底面积×高”能计算出圆柱的体积。
圆柱底面周长的一半
圆柱的高
底面
半径
拼成的长方体与圆来的圆柱有什么关系?
沿着高把圆柱切开再拼起来
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
圆柱体积计算公式是:
这个长方体的底面积等于圆柱的____________,高等于圆柱的____。
高
底面圆的面积
体积相等
笑笑了解到一根柱子的底面半径0.4 m,高为5 m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
3.14×0.42×5
=0.5024×5
=2.512(m3)
柱子的体积:
尝试解决下面的问题。
杯子的容积:
3.14×(6÷2)2×16
=28.26×16
=452.16(cm3)
452.16 cm3=452.16 mL
笑笑了解到一根柱子的底面半径0.4 m,高为5 m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
尝试解决下面的问题。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
底面半径:
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm3)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512cm3。
规范解答:
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
答:这根金箍棒重19.8448千克。
规范解答:
7.9×2512=19844.8(g)
19844.8g=19.8448kg
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
体积:
12.56×200=2512(cm3)
小 结
推导圆柱体积的计算公式
圆柱体积的计算公式
1.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
随堂小测
2. 一根圆柱形木料,底面积为 75 ,长 90 cm。
它的体积是多少?
答:它的体积是6750 cm3 。
规范解答:
圆柱的体积=圆柱底面积高
=7590
=6750()
圆柱的体积=底面积高
保温杯的容积:
50.24×15
=753.6 (cm?)
=0.7536(L)
所以带这杯水不够喝。
3. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量
底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,
带这杯水够喝吗?
保温杯的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2)
规范解答:
0.75361
4. 下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
10 cm
8 cm
杯子的容积:
50.24×10
=502.4 (cm3 )
=502.4 (mL)
杯子的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2 )
规范解答:
502.4498
答:所以杯子能装下这袋牛奶。
易错提醒
判断:圆柱的高不变,底面直径扩大到原来的4倍,体积也扩大到
原来的4倍。 ( )
错误解答
正确解答
√
×
错因分析:圆柱的高不变,底面半径、直径或者周长扩大到
原来的倍,则体积扩大到原来的倍。
判断:圆柱的高不变,底面直径扩大到原来的4倍,体积也扩大到
原来的4倍。 ( )
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
