北师大版数学九年级下册:1.5 三角函数的应用 课件(16张PPT)
文档属性
| 名称 | 北师大版数学九年级下册:1.5 三角函数的应用 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.5
三角函数的应用
《泰坦尼克号》
情景导入
泰坦尼克号叙述了一段浪漫凄美的爱情故事。泰坦尼克号的沉没让人感到遗憾,如果舵手能够分清方向、准确的计算距离,也许“泰坦尼克号”的结局是完美的
同学们,如果你是船长,怎样才能利用我们所学的知识来避免这样的灾难呢?本节课我们将一起讨论这个话题
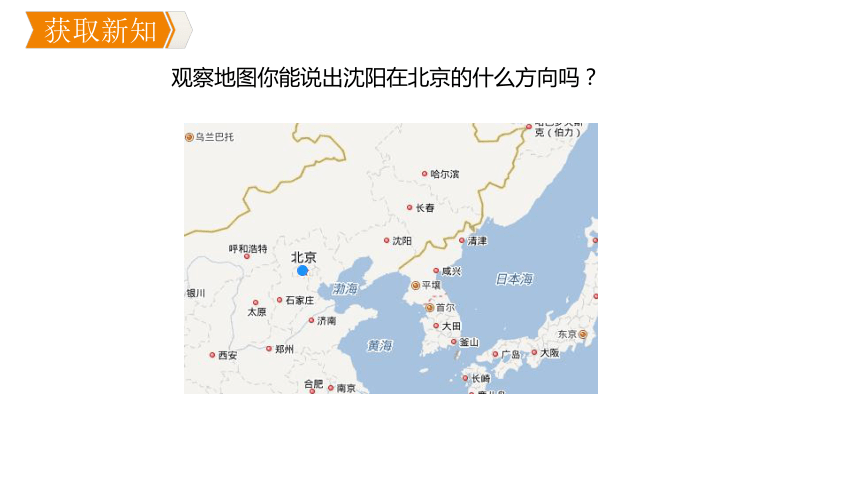
观察地图你能说出沈阳在北京的什么方向吗?
获取新知
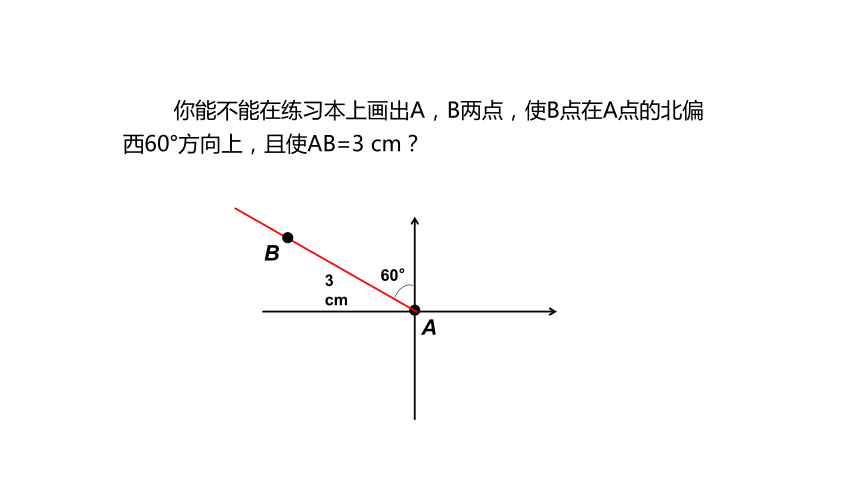
你能不能在练习本上画出A,B两点,使B点在A点的北偏西60°方向上,且使AB=3
cm?
A
60°
3
cm
B
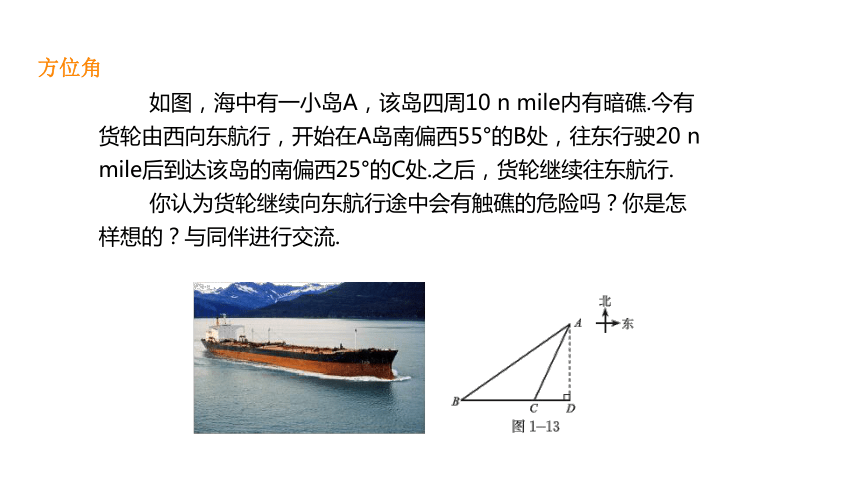
方位角
如图,海中有一小岛A,该岛四周10
n
mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20
n
mile后到达该岛的南偏西25°的C处.之后,货轮继续往东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
北
东
B
C
D
A
问题1:货轮要向正东方向继续行驶,有没有触礁的危险,由谁来决定?
分析:根据题意,小岛四周10
n
mile内有暗礁,那么货轮继续向东航行的方向如果到A的最短距离大于10
n
mile,则无触礁的危险;如果小于或者等于10
n
mile,则有触礁的危险.
A到BC所在直线的最短距离为过A作AD⊥BC,D为垂足,即AD的长度.我们需根据题意,计算出AD的长度,然后与10
n
mile比较.
问题2:如何求AD的长?
解:过A作BC的垂线,交BC的延长线于点D(如图),得到Rt△ABD和Rt
△ACD,从而BD=ADtan
55°,CD=ADtan
25°,由BD-CD=BC,BC=20
n
mile,得
ADtan
55°-
ADtan
25°=20,AD(tan
55°-tan
25°)=20,
北
东
B
C
D
A
因为20.79
n
mile>10
n
mile,所以货轮没有触礁的危险.
小结:
解决实际问题的关键是把实际问题转化为数学问题,根据题意画出示意图,将相关数据标注在图上,构造直角三角形,求解.
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50
m至B处.测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1
m)
解:在Rt△ADC中,
,即
在Rt△BDC中,
,即
∵AB=AC-BC=50,
∴
解得CD≈43(m),即塔CD的高度约为43
m.
想一想
问题引申:
如果考虑小明的身高呢?
如果设小明测量时,眼睛离地面的距离为1.6
m,其他数据不变,此时塔的高度为多少?你能画出示意图吗?
解:由前面的解答过程可知CC′≈43
m,
则CD≈43+1.6=44.6(m).
即考虑小明的身高,塔的高度约为44.6
m.
B
D
A
C
B′
A′
C′
30°
60°
练习1:如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
练习2:如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到中途,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程600km远了多少?
解:过点C作CD⊥AB于点D,
∵AD+BD=AB,
∴在Rt△BCD中,
∴AC+BC=
在Rt△ACD中,
750-600=150(km).
答:飞机的飞行路程比原来的路程600km远了150km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
谢
谢
观
看!
1.5
三角函数的应用
《泰坦尼克号》
情景导入
泰坦尼克号叙述了一段浪漫凄美的爱情故事。泰坦尼克号的沉没让人感到遗憾,如果舵手能够分清方向、准确的计算距离,也许“泰坦尼克号”的结局是完美的
同学们,如果你是船长,怎样才能利用我们所学的知识来避免这样的灾难呢?本节课我们将一起讨论这个话题
观察地图你能说出沈阳在北京的什么方向吗?
获取新知
你能不能在练习本上画出A,B两点,使B点在A点的北偏西60°方向上,且使AB=3
cm?
A
60°
3
cm
B
方位角
如图,海中有一小岛A,该岛四周10
n
mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20
n
mile后到达该岛的南偏西25°的C处.之后,货轮继续往东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
北
东
B
C
D
A
问题1:货轮要向正东方向继续行驶,有没有触礁的危险,由谁来决定?
分析:根据题意,小岛四周10
n
mile内有暗礁,那么货轮继续向东航行的方向如果到A的最短距离大于10
n
mile,则无触礁的危险;如果小于或者等于10
n
mile,则有触礁的危险.
A到BC所在直线的最短距离为过A作AD⊥BC,D为垂足,即AD的长度.我们需根据题意,计算出AD的长度,然后与10
n
mile比较.
问题2:如何求AD的长?
解:过A作BC的垂线,交BC的延长线于点D(如图),得到Rt△ABD和Rt
△ACD,从而BD=ADtan
55°,CD=ADtan
25°,由BD-CD=BC,BC=20
n
mile,得
ADtan
55°-
ADtan
25°=20,AD(tan
55°-tan
25°)=20,
北
东
B
C
D
A
因为20.79
n
mile>10
n
mile,所以货轮没有触礁的危险.
小结:
解决实际问题的关键是把实际问题转化为数学问题,根据题意画出示意图,将相关数据标注在图上,构造直角三角形,求解.
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50
m至B处.测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1
m)
解:在Rt△ADC中,
,即
在Rt△BDC中,
,即
∵AB=AC-BC=50,
∴
解得CD≈43(m),即塔CD的高度约为43
m.
想一想
问题引申:
如果考虑小明的身高呢?
如果设小明测量时,眼睛离地面的距离为1.6
m,其他数据不变,此时塔的高度为多少?你能画出示意图吗?
解:由前面的解答过程可知CC′≈43
m,
则CD≈43+1.6=44.6(m).
即考虑小明的身高,塔的高度约为44.6
m.
B
D
A
C
B′
A′
C′
30°
60°
练习1:如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
练习2:如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到中途,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程600km远了多少?
解:过点C作CD⊥AB于点D,
∵AD+BD=AB,
∴在Rt△BCD中,
∴AC+BC=
在Rt△ACD中,
750-600=150(km).
答:飞机的飞行路程比原来的路程600km远了150km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
谢
谢
观
看!
