1.5二次函数的应用课件(27张ppt)
文档属性
| 名称 | 1.5二次函数的应用课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 628.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第1章
二次函数
1.5
二次函数的应用
第1章
二次函数
1.5
二次函数的应用
考场对接
例题1
学校计划用地面砖铺设教学楼前矩形广场的地面ABCD,
已知矩形广场地面的长为100米,
宽为80米.
图案设计如图1-5-3所示,
广场的四角各有一个小正方形,
阴影部分为四个矩形,
四个矩形的宽都为小正方形的边长,
阴影部分铺蓝色地面砖,
其余部分铺白色地面砖.如果铺白色地面砖的费用为每平方米
30元,
铺蓝色地面砖的费用为每平方米20元,
当广
场四角的小正方形的边长为多少米时,
铺广场地
面的总费用最少?最少费用是多少?
题型一
利用二次函数解决最大(小)面积问题
考场对接
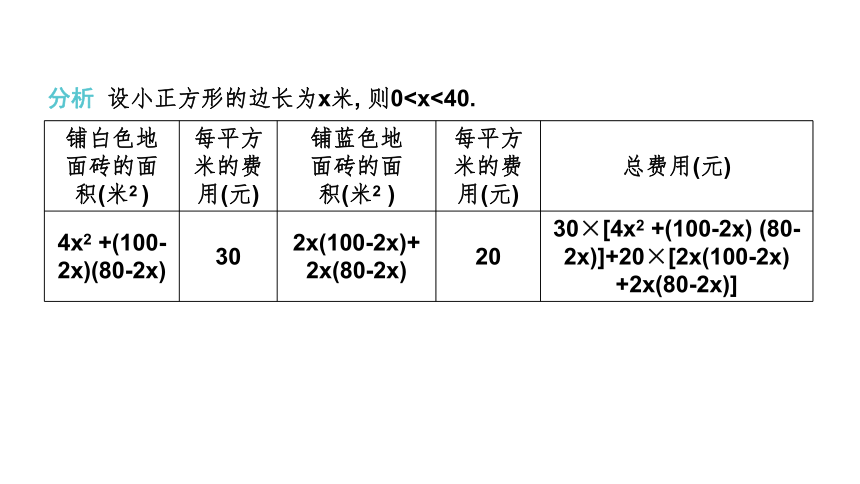
分析
设小正方形的边长为x米,
则0铺白色地
面砖的面
积(米2
)
每平方
米的费
用(元)
铺蓝色地
面砖的面
积(米2
)
每平方
米的费
用(元)
总费用(元)
4x2
+(100-2x)(80-2x)
30
2x(100-2x)+
2x(80-2x)
20
30×[4x2
+(100-2x)
(80-2x)]+20×[2x(100-2x)
+2x(80-2x)]
解:
设铺矩形广场地面的总费用为y元,
广场四角的小正方形的边长为x(0则y=30×[4x2
+(100-2x)(80-2x)]+20×[2x(100-
2x)+2x(80-2x)],
即y=80x2
-3600x+240
000,
配方得y=80(x-22.5)2
+199
500,
则当x=22.5时,
y的值最小,最小值为199
500.
答:当矩形广场四角的小正方形的边长为22.5米时,
铺广场地面的总费用最少,
最少费用为199
500元.
锦囊妙计
解决图形面积问题的一般步骤
(1)利用题目中的已知条件和我们学过的有关数学公式列出函数表达式;
(2)把函数表达式转化为二次函数的顶点式形式;
(3)根据二次函数自变量的取值范围求二次函数的最大值或最小值.
题型二
利用二次函数解决最大利润问题
例题2
襄阳市某企业积极响应政府“创新发展”的号召,
研发了一种新产品.已知研发、生产这种产品的成本为30元/件,
且年销
售量y(万件)关于售价x(元/件)的函数表达式为
-2x+140(40≤x<60),
y=
-x+80(60≤x≤70).
(1)若企业销售该产品获得的年利润为W(万元),
请直接写出年利润W(万元)关于售价x(元/件)的函数表达式;
(2)当该产品的售价x(元/件)为多少时,
企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,
试确定该产品的售价x(元/件)的取值范围.
解:
(1)当40≤x<60时,
W=(x-30)(-2x+140)=-
2x2
+
2
0
0
x
-
4
2
0
0
;
当
6
0
≤
x
≤
7
0
时
,W=(x-30)(-x+8
0
)
=
-
x2
+
1
1
0
x
-
2
4
0
0
,
即
-2x2
+200x-4200(40≤x<60),
W=
-x2
+110x-2400(60≤x≤70).
(2)由(1)知,
当40≤x<60时,
W=-2(x-50)
2+800.
∵-2<0,
∴当x=50时W有最大值800.
当60≤x≤70时,
W=-(x-55)2
+625.
∵-1<0,∴当60≤x≤70时W随x的增大而减小,
∴当x=60时,W有最大值600.
∵800>600,
∴当该产品的售价为50元/件时,
企业销售该产品获得的年利润最大,
最大年利润是800万元.
(3)当40≤x<60时,
令W=750,
得-2(x-50)2
+800=750,
解得x1
=45,
x2
=55.
由函数W=-2(x-50)
2
+800的性质可知,
当45≤x≤55时,
W≥750.
当60≤x≤70时,
W的最大值为600,
而600<750,
∴若企业销售该产品的年利润不少于750万元,
该产品的售价x(元/件)的取值范围为45≤x≤55.
锦囊妙计
解分段函数应用题的策略
对于分段函数,
已知函数值求自变量的取值时,
要将函数值分别代入各个函数中,
求出自变量的值,
并检验求出的自变量是否在其取值范围内,
若不在应舍去.
题型三
利用二次函数解决抛物线形问题
例题3
明珠大剧场坐落在聊城东昌湖西岸,
其上部为能够旋转的拱形钢结构,
并且具有开启、闭合功能,
全国独一无二,
如图1-5-4①.
舞台顶部横剖面拱形可近似看作抛物线的一部分,其中舞台高1.15米,
台口高13.5米,
台口宽29米,
如图②.以ED所在直线为x轴,
过拱顶点A且垂直于ED的直线
为y轴,
建立平面直角坐标系.
(1)求抛物线所表示的二次函数的表达式;
(2)舞台大幕悬挂在长度为20米的横梁MN上,
其下沿恰与舞台面接触,
求大幕的高度(精确到0.01米).
分析
(1)y轴是对称轴→设y=ax2
+c
(2)MN的长度→M,
N两点横
坐标→代入表达式求纵坐标
解题思路
解:
(1)由题设可知OA=13.5+1.15=14.65(米),OD=14.5米,
∴A(0,
14.65),
C(14.5,
1.15).
设抛物线所表示的二次函数的表达式为y=ax2
+c,
14.65=a·02
+c,
a=
,
则
解得
1.15=a·14.52
+c,
c=
14.65,
∴抛物线所表示的二次函数的表达式为y=
x2+14.65
.
(2)由MN=20米,
设点N的坐标为(10,
y0
),
将其代入二次函数表达式,
得y0
=
×102
+14.65≈8.229,
∴8.229-1.15=7.079≈7.08(米).
答:大幕的高度约为7.08米.
锦囊妙计
解决抛物线形问题的步骤
(1)建立合适的平面直角坐标系;(2)将实际问题中的数量转化为点的坐标;(3)设出抛物线的函数表达式,
并将点的坐标代入函数表达式中,
求出函数表达式;(4)利用函数表达式解决实际问题.
题型四
二次函数与一次函数的综合应用题
例题4
某公司研发了一款成本为60元/个的保温饭盒,
投放市场进行试销售,
按物价部门规定,其销售单价不低于成本,
但销售利润率不高于65%.经市场调研发现,
保温饭盒每天的销售数量y(个)与销售单价x(元/个)满足一次函数关系:当销售单价为70元/个时,
销售数量为160个;当销售单价为80元/个时,
销售数量为140个
(
利润率=
×100%
)
.
(1)求保温饭盒每天的销售数量y与销售单价x之间的函数表达式;
(2)当销售单价定为多少时,
公司每天获得的利润最大,
最大利润为多少元?
分析
(1)
原题信息
整理后信息
每天的销售数量y(个)与销售单价x(元/个)满足一次函数关系:当销售单价为70元/个时,
销售数量为160个;当销售单价为80元/个时,销售数量为140个
不妨设该函数表达式为y=kx+b,
当x=70时,
y=160;当x=80时,
y=140
(2)
原题信息
整理后信息
某公司研发了一款成本
为60元/个的保温饭盒,
销
售单价为x元/个,
每天的
销售数量为y个
设公司每天获得的利润为w元,
则w=(x-60)·y
其销售单价不低于成本,
但销售利润率不高于65%
x≥60,
列式可得
×
100%≤65%,
解得60≤x≤99
解:
(1)由题知,
保温饭盒每天的销售数量y与销售单价x满足一
次函数关系,
则可设该函数表达式为y=kx+b,
当x=70时,
y=160;
当x=80时,
y=140,将其代入函数表达式中,
70k+b=160,
k=-2,
得
解得
80k+b=140,
b=300.
由题知,
销售单价不低于成本,
但销售利润率不高于65%,
则有
x≥60,
×100%≤65%,
解得60≤x≤99,
∴y=-2x+300(60≤x≤99).
(2)设公司每天获得的利润为w元,
则w=(x-60)·y.
由(1)知y=-2x+300
(60≤x≤99),
∴w=(x-60)(-2x+300)=-2x2
+420x-18
000,
配方,
得w=-2(x-105)2
+4050,
∴当x=99时,
w最大,
wmax
=3978,
∴当销售单价定为99元/个时,
公司每天获得的利润最大,
最大利润为3978元.
锦囊妙计
解一次函数与二次函数综合应用题的策略
解决此类问题的关键是根据题意得出一次函数和二次函数的表达式,
然后由题意得出自变量的取值范围,
再结合自变量的取值范围,
求出二次函数的最值.
谢
谢
观
看!
第1章
二次函数
1.5
二次函数的应用
第1章
二次函数
1.5
二次函数的应用
考场对接
例题1
学校计划用地面砖铺设教学楼前矩形广场的地面ABCD,
已知矩形广场地面的长为100米,
宽为80米.
图案设计如图1-5-3所示,
广场的四角各有一个小正方形,
阴影部分为四个矩形,
四个矩形的宽都为小正方形的边长,
阴影部分铺蓝色地面砖,
其余部分铺白色地面砖.如果铺白色地面砖的费用为每平方米
30元,
铺蓝色地面砖的费用为每平方米20元,
当广
场四角的小正方形的边长为多少米时,
铺广场地
面的总费用最少?最少费用是多少?
题型一
利用二次函数解决最大(小)面积问题
考场对接
分析
设小正方形的边长为x米,
则0
面砖的面
积(米2
)
每平方
米的费
用(元)
铺蓝色地
面砖的面
积(米2
)
每平方
米的费
用(元)
总费用(元)
4x2
+(100-2x)(80-2x)
30
2x(100-2x)+
2x(80-2x)
20
30×[4x2
+(100-2x)
(80-2x)]+20×[2x(100-2x)
+2x(80-2x)]
解:
设铺矩形广场地面的总费用为y元,
广场四角的小正方形的边长为x(0
+(100-2x)(80-2x)]+20×[2x(100-
2x)+2x(80-2x)],
即y=80x2
-3600x+240
000,
配方得y=80(x-22.5)2
+199
500,
则当x=22.5时,
y的值最小,最小值为199
500.
答:当矩形广场四角的小正方形的边长为22.5米时,
铺广场地面的总费用最少,
最少费用为199
500元.
锦囊妙计
解决图形面积问题的一般步骤
(1)利用题目中的已知条件和我们学过的有关数学公式列出函数表达式;
(2)把函数表达式转化为二次函数的顶点式形式;
(3)根据二次函数自变量的取值范围求二次函数的最大值或最小值.
题型二
利用二次函数解决最大利润问题
例题2
襄阳市某企业积极响应政府“创新发展”的号召,
研发了一种新产品.已知研发、生产这种产品的成本为30元/件,
且年销
售量y(万件)关于售价x(元/件)的函数表达式为
-2x+140(40≤x<60),
y=
-x+80(60≤x≤70).
(1)若企业销售该产品获得的年利润为W(万元),
请直接写出年利润W(万元)关于售价x(元/件)的函数表达式;
(2)当该产品的售价x(元/件)为多少时,
企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,
试确定该产品的售价x(元/件)的取值范围.
解:
(1)当40≤x<60时,
W=(x-30)(-2x+140)=-
2x2
+
2
0
0
x
-
4
2
0
0
;
当
6
0
≤
x
≤
7
0
时
,W=(x-30)(-x+8
0
)
=
-
x2
+
1
1
0
x
-
2
4
0
0
,
即
-2x2
+200x-4200(40≤x<60),
W=
-x2
+110x-2400(60≤x≤70).
(2)由(1)知,
当40≤x<60时,
W=-2(x-50)
2+800.
∵-2<0,
∴当x=50时W有最大值800.
当60≤x≤70时,
W=-(x-55)2
+625.
∵-1<0,∴当60≤x≤70时W随x的增大而减小,
∴当x=60时,W有最大值600.
∵800>600,
∴当该产品的售价为50元/件时,
企业销售该产品获得的年利润最大,
最大年利润是800万元.
(3)当40≤x<60时,
令W=750,
得-2(x-50)2
+800=750,
解得x1
=45,
x2
=55.
由函数W=-2(x-50)
2
+800的性质可知,
当45≤x≤55时,
W≥750.
当60≤x≤70时,
W的最大值为600,
而600<750,
∴若企业销售该产品的年利润不少于750万元,
该产品的售价x(元/件)的取值范围为45≤x≤55.
锦囊妙计
解分段函数应用题的策略
对于分段函数,
已知函数值求自变量的取值时,
要将函数值分别代入各个函数中,
求出自变量的值,
并检验求出的自变量是否在其取值范围内,
若不在应舍去.
题型三
利用二次函数解决抛物线形问题
例题3
明珠大剧场坐落在聊城东昌湖西岸,
其上部为能够旋转的拱形钢结构,
并且具有开启、闭合功能,
全国独一无二,
如图1-5-4①.
舞台顶部横剖面拱形可近似看作抛物线的一部分,其中舞台高1.15米,
台口高13.5米,
台口宽29米,
如图②.以ED所在直线为x轴,
过拱顶点A且垂直于ED的直线
为y轴,
建立平面直角坐标系.
(1)求抛物线所表示的二次函数的表达式;
(2)舞台大幕悬挂在长度为20米的横梁MN上,
其下沿恰与舞台面接触,
求大幕的高度(精确到0.01米).
分析
(1)y轴是对称轴→设y=ax2
+c
(2)MN的长度→M,
N两点横
坐标→代入表达式求纵坐标
解题思路
解:
(1)由题设可知OA=13.5+1.15=14.65(米),OD=14.5米,
∴A(0,
14.65),
C(14.5,
1.15).
设抛物线所表示的二次函数的表达式为y=ax2
+c,
14.65=a·02
+c,
a=
,
则
解得
1.15=a·14.52
+c,
c=
14.65,
∴抛物线所表示的二次函数的表达式为y=
x2+14.65
.
(2)由MN=20米,
设点N的坐标为(10,
y0
),
将其代入二次函数表达式,
得y0
=
×102
+14.65≈8.229,
∴8.229-1.15=7.079≈7.08(米).
答:大幕的高度约为7.08米.
锦囊妙计
解决抛物线形问题的步骤
(1)建立合适的平面直角坐标系;(2)将实际问题中的数量转化为点的坐标;(3)设出抛物线的函数表达式,
并将点的坐标代入函数表达式中,
求出函数表达式;(4)利用函数表达式解决实际问题.
题型四
二次函数与一次函数的综合应用题
例题4
某公司研发了一款成本为60元/个的保温饭盒,
投放市场进行试销售,
按物价部门规定,其销售单价不低于成本,
但销售利润率不高于65%.经市场调研发现,
保温饭盒每天的销售数量y(个)与销售单价x(元/个)满足一次函数关系:当销售单价为70元/个时,
销售数量为160个;当销售单价为80元/个时,
销售数量为140个
(
利润率=
×100%
)
.
(1)求保温饭盒每天的销售数量y与销售单价x之间的函数表达式;
(2)当销售单价定为多少时,
公司每天获得的利润最大,
最大利润为多少元?
分析
(1)
原题信息
整理后信息
每天的销售数量y(个)与销售单价x(元/个)满足一次函数关系:当销售单价为70元/个时,
销售数量为160个;当销售单价为80元/个时,销售数量为140个
不妨设该函数表达式为y=kx+b,
当x=70时,
y=160;当x=80时,
y=140
(2)
原题信息
整理后信息
某公司研发了一款成本
为60元/个的保温饭盒,
销
售单价为x元/个,
每天的
销售数量为y个
设公司每天获得的利润为w元,
则w=(x-60)·y
其销售单价不低于成本,
但销售利润率不高于65%
x≥60,
列式可得
×
100%≤65%,
解得60≤x≤99
解:
(1)由题知,
保温饭盒每天的销售数量y与销售单价x满足一
次函数关系,
则可设该函数表达式为y=kx+b,
当x=70时,
y=160;
当x=80时,
y=140,将其代入函数表达式中,
70k+b=160,
k=-2,
得
解得
80k+b=140,
b=300.
由题知,
销售单价不低于成本,
但销售利润率不高于65%,
则有
x≥60,
×100%≤65%,
解得60≤x≤99,
∴y=-2x+300(60≤x≤99).
(2)设公司每天获得的利润为w元,
则w=(x-60)·y.
由(1)知y=-2x+300
(60≤x≤99),
∴w=(x-60)(-2x+300)=-2x2
+420x-18
000,
配方,
得w=-2(x-105)2
+4050,
∴当x=99时,
w最大,
wmax
=3978,
∴当销售单价定为99元/个时,
公司每天获得的利润最大,
最大利润为3978元.
锦囊妙计
解一次函数与二次函数综合应用题的策略
解决此类问题的关键是根据题意得出一次函数和二次函数的表达式,
然后由题意得出自变量的取值范围,
再结合自变量的取值范围,
求出二次函数的最值.
谢
谢
观
看!
