第1章二次函数复习课件（117张ppt）

(共117张PPT)
第1章
二次函数
章末复习
第1章
二次函数
章末复习
知识框架
归纳整合
素养提升
中考链接
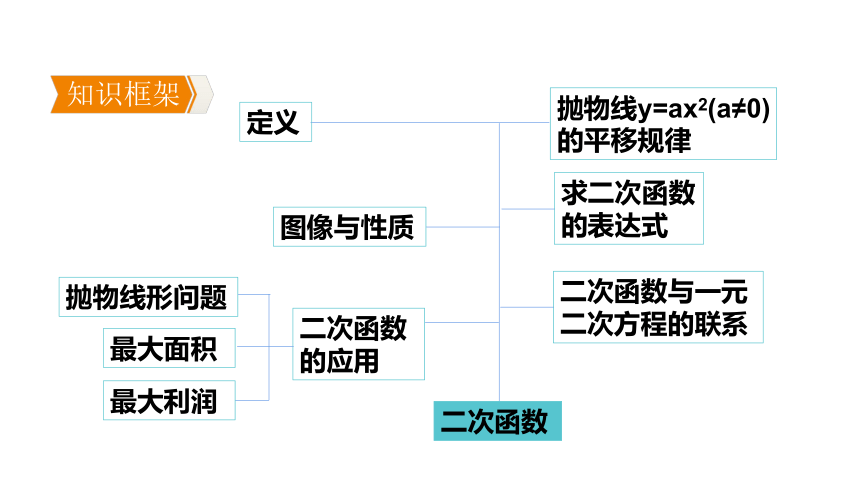
知识框架
图像与性质
二次函数的应用
二次函数
抛物线y=ax2(a≠0)
的平移规律
二次函数与一元二次方程的联系
抛物线形问题
最大面积
最大利润
定义
求二次函数
的表达式
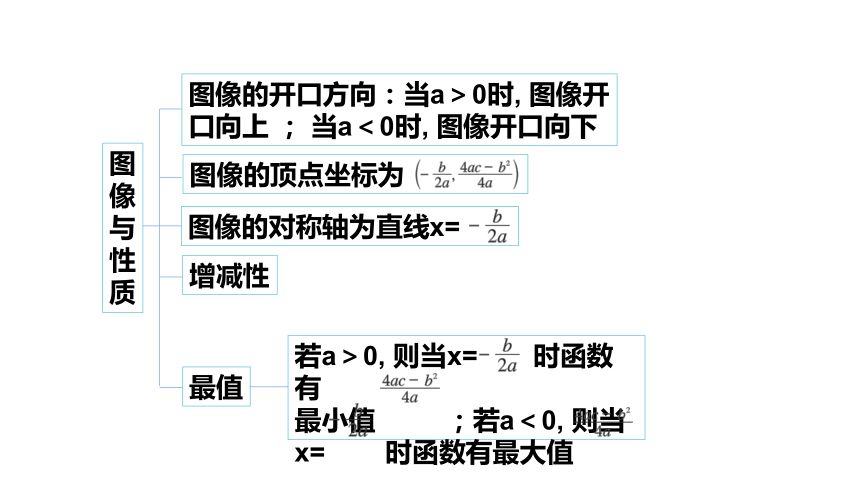
图像的顶点坐标为
图像的对称轴为直线x=
增减性
图
像
与
性
质
图像的开口方向：当a＞0时,
图像开
口向上
；
当a＜0时,
图像开口向下
最值
若a＞0,
则当x=
时函数有
最小值
；若a＜0,
则当x=
时函数有最大值
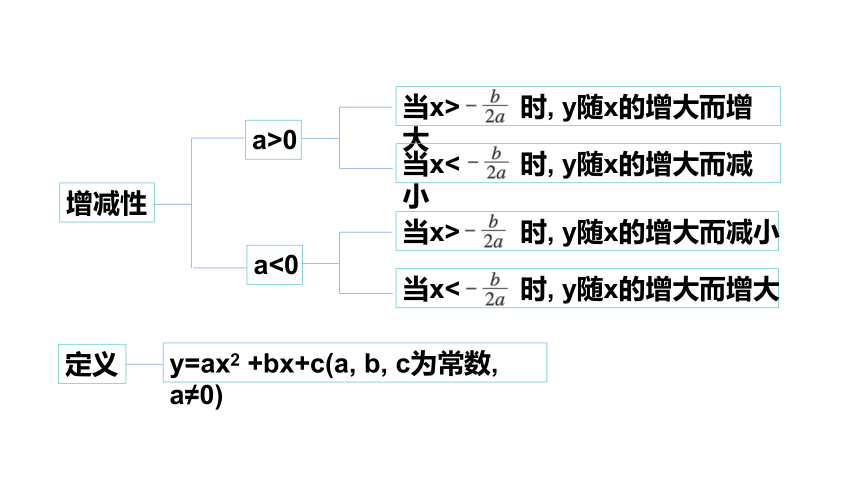
当x>
时,
y随x的增大而增大
当x<
时,
y随x的增大而减小
增减性
当x>
时,
y随x的增大而减小
当x<
时,
y随x的增大而增大
a>0
a<0
定义
y=ax2
+bx+c(a,
b,
c为常数,
a≠0)
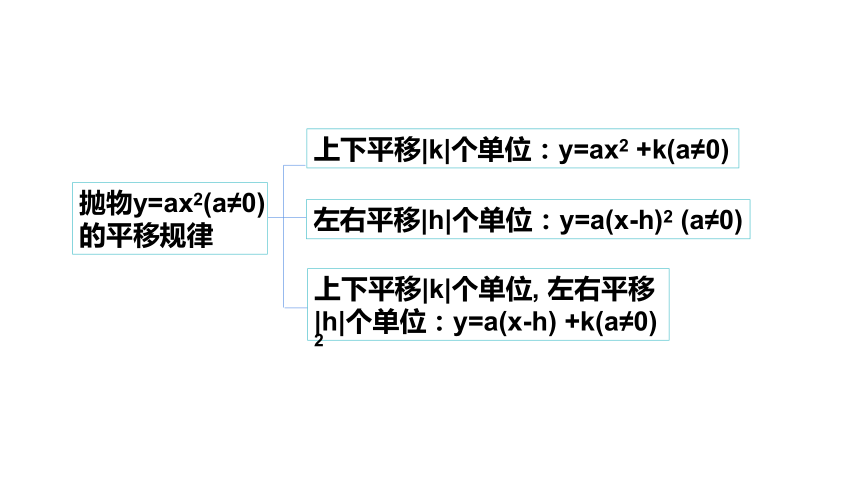
上下平移|k|个单位：y=ax2
+k(a≠0)
左右平移|h|个单位：y=a(x-h)2
(a≠0)
上下平移|k|个单位,
左右平移|h|个单位：y=a(x-h)
+k(a≠0)
2
抛物y=ax2(a≠0)
的平移规律
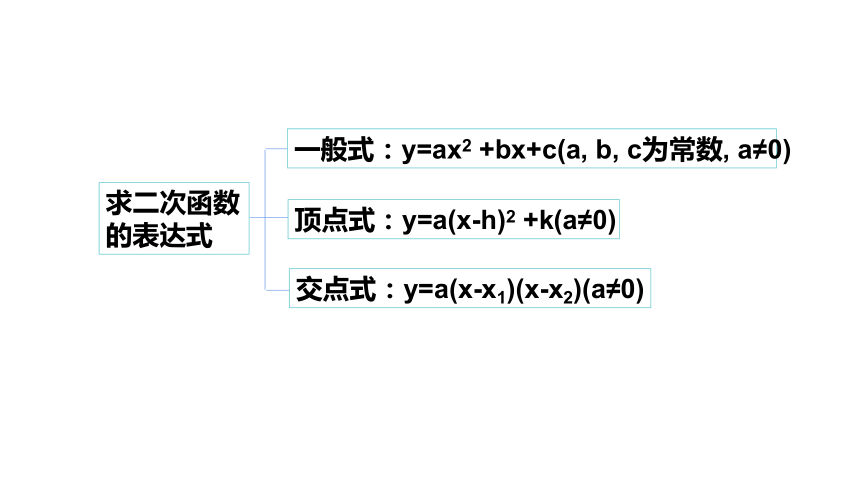
一般式：y=ax2
+bx+c(a,
b,
c为常数,
a≠0)
顶点式：y=a(x-h)2
+k(a≠0)
交点式：y=a(x-x1)(x-x2)(a≠0)
求二次函数
的表达式
抛物线与x轴交点的横坐标是相应方程的解
抛物线与x轴的交点个数和判别式的关系
用图像法解一元二次方程
二次函数与
一元二次方
程的联系
【要点指导】根据二次函数y=ax2
+bx+c的图像确定有关代数式的符号是二次函数中的一类典型的数形结合问题,
具有较强的推理性．解题时应注意a决定抛物线的开口方向,
c决定抛物线与y轴的交点位置,
抛物线的对称轴由a,
b共同决定,
b2
-4ac决定抛物线与x轴的交点情况.
x=1时的函数值决定a+b+c的符号,
x=-1时的函数值决定a-b+c的符号.
在此基础上,
还可推出其他代数式的符号.
运用数形结合的思想更直观、更简捷．
归纳整合
专题一
二次函数的图像与系数的关系
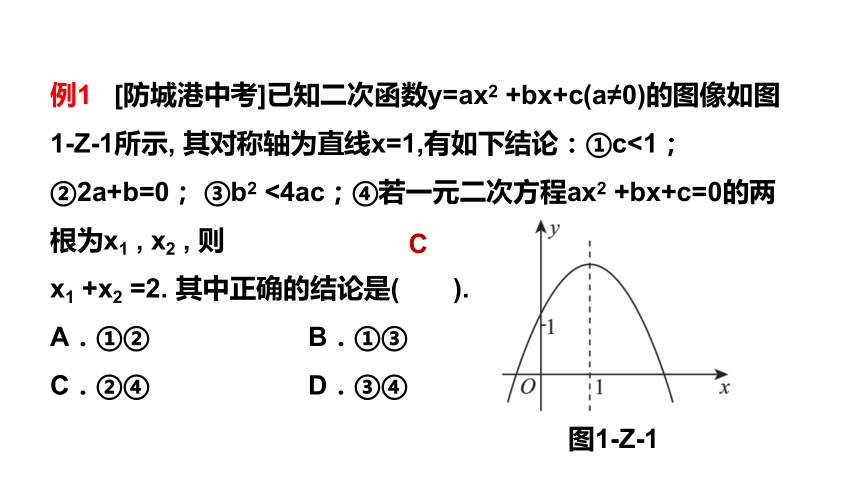
例1
[防城港中考]已知二次函数y=ax2
+bx+c(a≠0)的图像如图1-Z-1所示,
其对称轴为直线x=1,有如下结论：①c<1；②2a+b=0；
③b2
<4ac；④若一元二次方程ax2
+bx+c=0的两根为x1
,
x2
,
则
x1
+x2
=2.
其中正确的结论是(　　).
A．①②　　　
B．①③　　　
C．②④　　　
D．③④
图1-Z-1
C
分析
抛物线与y轴的交点在点(0,
1)的上方,
故c＞1,
∴①错；
对称轴为直线x=
=1,
变形得2a+b=0,
∴②对；
抛物线与x轴有两个不同的交点,
∴b2
-4ac>0,
即b2
>4ac,
∴③错；
根据抛物线的轴对称性可知关于对称轴对称的点到对称轴的距离相等,
∴其对称轴为直线x=
,
(x1
,
x2
分别是关于对称轴对称的点的横坐标),
若一元二次方程ax2
+bx+c=0的两根为x1
,
x2
,则x=
=1,可化为x1
+x2
=2,
∴④对.
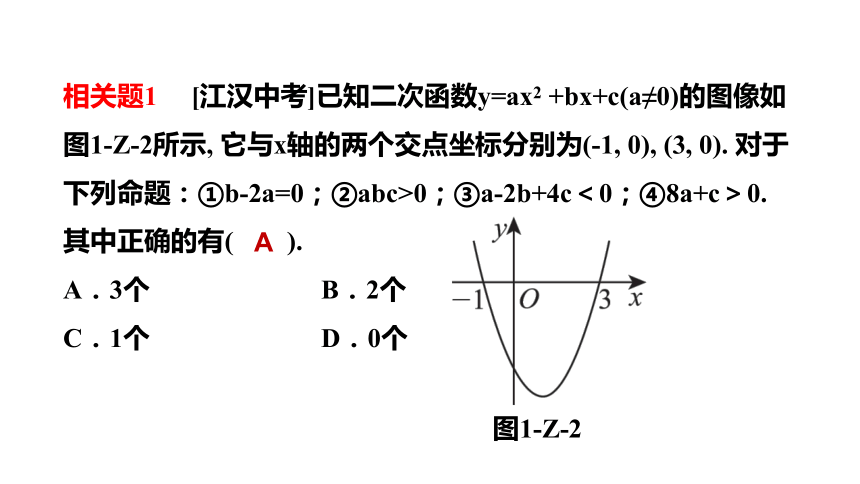
相关题1
[江汉中考]已知二次函数y=ax2
+bx+c(a≠0)的图像如图1-Z-2所示,
它与x轴的两个交点坐标分别为(-1,
0),
(3,
0).
对于下列命题：①b-2a=0；②abc>0；③a-2b+4c＜0；④8a+c＞0.
其中正确的有(　　).
A．3个
B．2个
C．1个
D．0个
图1-Z-2
A
【要点指导】利用待定系数法求二次函数的表达式,
在设函数表达式时,
可以根据题目所给出的条件选择不同的形式：①一般式：y=ax2
+bx+c(a≠0),
当已知条件是三个普通点时,
可选择一般式；②顶点式：y=a(x-h)2
+k(a≠0),
当已知条件是顶点和一个普通点时,
可选择顶点式；③交点式：y=a(x-x1
)(x-x2
)(a≠0),
其中x1
,
x2
是抛物线与x轴交点的横坐标,
当已知条件是抛物线与x轴的两个交点及一个普通点时,
可选择交点式.
专题二
用待定系数法求二次函数的表达式
例2
根据下列条件,
分别求出对应的二次函数的表达式．
(1)已知抛物线的顶点为(-1,
-2),
且经过点(1,
10)；
(2)已知抛物线经过点A(0,
1),
B(2,
4),
C(3,
10)；
(3)已知抛物线与x轴交于点(3,
0),
(5,
0),
且经过点(0,
1).
分析
解：(
1)设抛物线所表示的函数表达式为y=a(x+1)2
-2,
将(1,
10)代入,
得10=a(1+1)2
-2,
解得a=3,
所以抛物线所表示的函数表达式为y=3x2
+6x+1.
(2)设抛物线所表示的函数表达式为y=ax2
+bx+c,
将A(0,
1),
B(2,
4),
C(3,10)三点坐标代入,
1=c,
得
4=4a+2b+c,
解得a=
,
b=-
,
c=1,
10=9a+3b+c,
所以抛物线所表示的函数表达式为y=
x2
-
x+1.
(3)设抛物线所表示的函数表达式为y=a(x-3)(x-5),
将(0,
1)代入,
得
1=a×(0-3)×(0-5),
解得a=
,
所以抛物线所表示的函数表达式为y=
x+1.
相关题2-1
已知抛物线与x轴的交点是A(-2,
0),
B(1,
0),
且经过点C(2,
8).
(1)求该抛物线所表示的函数表达式；
(2)
求该抛物线的顶点坐标.
相关题2-2
已知二次函数y=ax2
+bx+c的图像上部分点的坐标(x,
y)满足下表：
(1)求这个二次函数的表达式；
(2)用配方法求出这个二次函数图像的顶点坐标和对称轴．
x
…
-1
0
1
2
…
y
…
-4
-2
2
8
…
【要点指导】对于二次函数y=ax2
+bx+c(a≠0),
当y=0时,
就变成了
一元二次方程ax2
+bx+c=0(a≠0).
当二次函数y=ax2
+bx+c的图像与x轴有交点时,
其交点横坐标就是一元二次方程ax2
+bx+c=0的解.
二次函数y=ax2
+bx+c的图像与x轴的交点有三种情况：图像与x轴有两个不同的交点?一元二次方程ax2
+bx+c=0有两个不相等的实根；图像与x轴有两个相同的交点?一元二次方程ax2
+bx+c=0有两个相等的实根；图像与x轴没有交点?一元二次方程ax2
+bx+c=0没有实数根.
专题三
二次函数与一元二次方程的关系
例3
已知二次函数y=2(k+1)x2
+4kx+2k-3,
求：
(1)当k为何值时,
二次函数y=2(k+1)x2
+4kx+2k-3的图像与x轴有两个不同的交点？有两个相同的交点？没有交点？
(2)当k为何值时,
二次函数y=2(k+1)x2
+4kx+2k-3的图像与x轴的两个不同的交点分别在原点的两侧？
解：(1)b2
-4ac=(4k)2
-4×2(k+1)(2k-3)=16k2
-8(2k2
-k-3)=8k+24.
当8k+24>0且2(k+1)≠0,
即k>-3且k≠-1时,
二次函数的图像与x轴有两个不同的交点；
当8k+24=0且2(k+1)≠0,
即k=-3时,
二次函数的图像与x轴有两个相同的交点；
当8k+24<0且2(k+1)≠0,
即k<-3时,
二次函数的图像与x轴没有交点.
(2)设二次函数y=2(k+1)x2
+4kx+2k-3的图像与x轴的两个不同的交点的横坐标分别为x1
,
x2
.
∵二次函数y=2(k+1)x2
+4kx+2k-3的图像与x轴的两个不同的交点分别在原点的两侧,
则有b2
-4ac>0,
且x1
x2
<0.
又b2
-4ac=8k+24,
x1
x2
=
,
8k+24>0,
∴
<0,
解得-1,
∴当-1时,
二次函数y=2(k+1)x2
+4kx+2k-3的图像与x轴的两个不同的交点分别在原点的两侧.
相关题3-1
已知二次函数y=x2
-6x+(2m+1)与x轴有交点．
(1)求m的取值范围；
(2)如果该二次函数的图
像
与
x
轴
的
交
点
分别为(x1
,
0),
(x2
,
0),
且2x1
x2+x1+x2
≥20,
求m的取值范围．
解：(1)∵二次函数y＝x2－6x＋(2m＋1)与x轴有交点，
∴Δ≥0，∴(－6)2－4(2m＋1)≥0，解得m≤4.
(2)∵二次函数y＝x2－6x＋(2m＋1)的图像与x轴的交点分别为
(x1，0)，(x2，0)，
∴x1，x2是方程x2－6x＋(2m＋1)＝0的两个根，
∴x1＋x2＝6，x1x2＝2m＋1.
∵2x1
x2＋x1＋x2≥20，∴2(2m＋1)＋6≥20，
∴m≥3，由(1)知m≤4，∴m的取值范围是3≤m≤4.
相关题3-2
已知：关于x的函数y=kx2
+k2
x-2的图像与y轴
交于点C．
(1)当k=-2时,
求该函数图像与x轴的公共点的个数；
(2)若该函数图像与x轴有一个交点为A,
当△
A
O
C
是
等
腰
三
角
形时，求k的值；
(3)若x≥1时函数值y随着x的增大而减小,
求k的取值范围.
解：
(1)方法一：当k＝－2时，函数为y＝－2x2＋4x－2.
∵b2－4ac＝42－4×(－2)×(－2)＝0，
∴函数图像与x轴的公共点只有一个．
方法二：当k＝－2时，函数为y＝－2x2＋4x－2.
令y＝0，则－2x2＋4x－2＝0，
解得x1＝x2＝1，
∴该函数图像与x轴的公共点只有一个．
【要点指导】解答二次函数与三角形或四边形的综合题的关键在于充分利用几何图形的性质及题设,
挖掘几何图形中隐含的条件,
在复杂的“背景”下辨认、分解基本图形或通过添加辅助线补全或构造基本图形,并善于联想所学知识,
突破思维障碍,
合理运用方程等数学思想解决问题.
专题四
二次函数与三角形或四边形的综合题
例4
如图1-Z-3所示,
已知抛物线的对称轴是y轴,
且点(2,
2),
(
1,
)
在抛物线上,
P是抛物线上不与顶点N重合的一动点,
过点P作PA⊥x轴于点A,
PC⊥y轴于C,
延长PC交抛物线于点E,
设点M是点O关于抛物线顶点N的对称点,
D是点C关于点N的对称点.
(1)求抛物线所表示的函数表达式及顶点N的坐标；
(2)求证：四边形PMDA是平行四边形；
(3)求证：△DPE∽△PAM,
并求出当它们的相似
比为
3时点P的坐标.
图1-Z-3
解：(1)∵抛物线的对称轴是y轴,
∴设抛物线所表示的函数表达式为y=ax2
+c.
把点(2,
2),
(
1,
)
代入,
2=4a+c,
a=
,
得
解得
=a+c,
c=1,
∴抛物线所表示的函数表达式为y=
x2
+1.
∵当x=0时,
y=1,
∴N(0,
1)．
(2)∵PA⊥x轴,
点M,
D在y轴上,
∴PA∥DM.
∵易知四边形PCOA是矩形,
∴PA=CO.
∵点C与点D关于点N对称,
点M与点O关于点N对称,
∴DN=CN,ON=MN,
∴DN+MN=CN+ON,
即DM=CO=PA,
∴四边形PMDA是平行四边形．
(3)设P
(
x,
x2
+1
)
,
MA与PD交于点G,
如图1-Z-3,
则PC=OA=x,
PA=CO=
x2
+1,
CM=
x2
-1.
根据勾股定理,
得PM=
=
x2
+1,
∴PM=PA.
∵四边形PMDA是平行四边形,
∴四边形PMDA是菱形,
∴∠APM=2∠APD．∵PE⊥y轴,
y轴是抛物线的对称轴,
∴点P,
E关于y轴对称,
∴PD=DE,
∴∠PDC=∠EDC,
∴∠PDE=2∠PDC．
∵PA∥DM,
∴∠APD=∠PDC,
∴∠APM=∠PDE．
又∵
,
∴△DPE∽△PAM．
∵四边形PMDA是菱形,
PD⊥AM,
PG=
PD,
当相似比为
时,
,
∴
,
∴∠PAG=60°,
∴∠MAO=30°,PA=AM．
∵MO=2ON=2,
∴OA=
,
∴PA=AM=4,
即P(
,
4).
相关题4
[益阳中考]如图1-Z-4,
直线y1
=－3x+3与x轴、y轴分别交于点A,
B,
抛物线y2
=a(x－2)2
+k经过点A,
B,
且与x轴交于另一点C,
其顶点为P．
(1)求a,
k的值；
(2)抛物线的对称轴上有一点Q,
使△ABQ
是以AB为底边的等腰三角形,求点Q的坐标；
(3)在抛物线及其对称轴上分别取点M,
N,
使以A,C,
M,
N为顶点的四边形为正方形,
求此正方形的边长.
图1-Z-4
(2)如图所示，设点Q的坐标为(2,
m)，对称轴x＝2交x轴于点F，过点B作BE垂直于直线x＝2
于点E.在Rt△AQF中，AF＝1，QF＝m，∴AQ2＝AF2＋QF2＝1＋m2.
在Rt△BQE中，BE＝2，EQ＝3－m，
∴BQ2＝BE2＋EQ2＝4＋(3－m)2.
∵△ABQ是以AB为底边的等腰三角形，
∴AQ＝BQ，
∴1＋m2＝4＋(3－m)2，∴m＝2，∴点Q的坐标为(2,
2)．
【要点指导】
运用建模思想,
将实际问题中的信息语言转换成数学语言,
抽象、归纳出其中的数量关系,
将实际问题转化为数学问题,
从而运用二次函数的有关知识加以解决．
专题五
二次函数的实际应用
例5
[济宁中考]某商店经销一种双肩包,
已知这种双肩包的成本价为每个30元.
经市场调查发现,
这种双肩包每天的销售量y(单位：个)与销售单价x(单位：元/个)有如下关系：y=-x+60(30≤x≤60),
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数表达式；
(2)这种双肩包的销售单价定为多少时,
每天的销售利润最大
最大利润是多少元？
(3)若物价部门规定这种双肩包的销售单价不高于48元/个,
该商店销售这种双肩包每天要获得200元的销售利润,
则销售单价应定为多少？
解：
(1)根据题意,
得w=(x-30)·y=(x-30)(-x+60)=-x2
+90x-1800,
∴w与x的函数表达式为w=-x2
+90x-1800
(30≤x≤60).
(2)w=-x2
+90x-1800=-(x-45)2
+225(30≤x≤60).
∵-1<0,
∴当x=45时,
w有最大值,
最大值为225.
答：这种双肩包的销售单价定为45元/个时,
每天的销售利润最大,
最大利润是225元.
(3)当w=200时,
可得方程-(x-45)2
+225=200.
解得x1
=40,
x2
=50.
∵50>48,
∴x2
=50不符合题意,
应舍去．
答：该商店销售这种双肩包每天要获得200元的销售利润,
则销售单价应定为40元/个．
相关题5
某农场拟建一间矩形种牛饲养室,
饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50
m.
设饲养室长为x(m),
占地面积为y(m2).
(1)如图1-Z-5①,
求饲养室的长x为多少时,
占地面积y最大；
图1-Z-5
相关题5
某农场拟建一间矩形种牛饲养室,
饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50
m.
设饲养室长为x(m),
占地面积为y(m2).
(2)如图②,
现要求在图中所示位置留2
m宽的门,
且仍使饲养室的占地面积最大,
小敏说：“只要饲养室长比
(1)中的长多2
m就行了．”请你通过计算,
判断小敏的说法是否正确．
图1-Z-5
【要点指导】数形结合思想就是在研究问题时把数与形结合起来考虑,
即把问题的数量关系转化为图形的性质,
或者把图形的性质转化为数量关系来考虑,
从而使复杂的问题简单化,
抽象的问题具体化.
素养提升
专题一
数形结合思想
例1
已知抛物线y=ax2
+bx+c的对称轴是经过点(2,
0)且与y轴平行的直线,
抛物线与x轴相交于点A(1,0),
与y轴相交于点B(0,
3),
其在对称轴左侧的图像如图1-Z-6所示．
(1)求抛物线所表示的二次函数的表达式,
并写出抛物线的顶点坐标；
(2)画出抛物线在对称轴右侧的图像,
并根
据图像,
写出当x为何值时,y＜0.
图1-Z-6
分析
(1)由抛物线与y轴交于点B(0,
3),
可得出c=3,
然后将A(1,
0)代入
抛物线所表示的函数表达式中,
可得出a+b+3=0,
而抛物线的对称轴是直线x=
=2,
可联立两个关于a,
b的方程组成方程组,
通过解方程组可求出a,
b的值,
也就得出了抛物线所表示的二次函数的表达式.
(2)根据对称轴为直线x=2可得出函数图像与x轴的另一个交点的坐标为
(3,
0),
由于抛物线开口向上,
可得出当1＜x＜3时,
y＜0.
解：
(1)由题意,
得c=3,
a+b+3=0,
=2,
即b=-4a.
a+b+3=0,
a=1,
解方程组
得
b=-4a,
b=-4,
∴抛物线所表示的二次函数的表达式为y=x2
-4x+3．
当x=2时,
y=-1,
则抛物线的顶点坐标为(2,
-1).
(2)图像如图1-Z-7所示,
由图像,
得当1＜x＜3时,
y＜0．
图1-Z-7
相关题1
已
知
：
如
图
1
-
Z
-
8
,A(-1,
0),
B(2,
-3)两点在一次函数y1
=-x+m与二次函数y2
=ax2
+bx-3的图像上.
(1)求m的值和二次函数的表达式；
(2)请直接写出使y1
＞y2成立的自
变量x的取值范围.
图1-Z-8
【要点指导】方程思想就是对所求问题通过列方程(组)来求解的思想方法,
方程思想在二次函数这一章中主要体现在求二次函数的表达式.
专题二
方程思想
例2
[邵阳中考]如图1-Z-9所示,
顶点为
(
，
)
的抛物线y=ax2
+bx+c过点M(2,
0).
(1)求抛物线所表示的函数表达式；
(2)A是抛物线与x轴的交点(不与点M重合),
B是抛物线与y轴的交点,
C是直线y=x+1上
的一点(处于x轴下方),
D是反比例函数y=
(k>0)的图像上一点,
若以A,
B,
C,
D为顶点
的四边形是菱形,
求k的值.
图1-Z-9
解：(1)依题意可设抛物线所表示的函数表达式为y=a
(
x-
)2
,
将点M(2,
0)代入,
可得a
(
2-
)2
=0,
解得
a=1,
∴抛物线所表示的函数表达式为y=
(
x-
)2
.
(2)当y=0时,
(
x-
)
2
=0,
解得x1
=-1,
x2
=2,
∴A(-1,
0).
当x=0时,y=
(
0-
)2
=-2,
∴B(0,
-2),
∴在Rt△OAB
中,
OA=1,
OB=2,
∴
AB=
5．
设直线y=x+1与y轴的交点为G,
易求G(0,
1),
∴Rt△AOG
为等腰直角三角形,∴∠AGO=45°.
∵k>0,
∴y=
的图像位于第一、三象限,
故点D只能在一、三象限．又∵点C在直线y=x+1上且在x轴下方,
∴符合条件的菱形只能有如下两种情况：
①此菱形以AB
为边且AC
也为边,
如图1-Z-10所示,
过点D作N⊥y轴于点N．在Rt△BDN
中,
易知∠DBN=∠AGO=45°,
BD=AB=
,
∴DN=BN=
,
∴D
．
∵点D在函数y=
(k>0)的图像上,
∴k=
．
②此菱形以AB为对角线,
如图1-Z-11所示,作AB的垂直平分线CD交直线y=x+1于点C,
交y=
的图像于点D.
再分别过点D,
B作DF⊥x轴于点F,作BE⊥DF,
交DF的延长线于点
E.
在Rt△BDE
中,
同①可证∠AGO=∠DBO=∠BDE=45°,
∴BE=DE.
可设点D的坐标为(x,
x-2).
∵BE2
+DE2
=BD2
,
∴BD=
BE=
x．
∵四边形
ACBD
是菱形,
∴AD=BD=
x,
∴在Rt△ADF
中,
AD2
=AF2
+DF2
,
即(
x)2
=(x+1)2
+(x-2)2
,
解得x=
,
则点D
的坐标为
.
∵点D在y=
(k>0)的图像上,
∴k=
．
综上所述,
k的值为
或
．
相关题2
如图1-Z-12,
在平面直角坐标系中,
OB⊥OA,且OB=2OA,
点A的坐标是(-1,
2).
(1)求点B的坐标；
(2)求过A,
O,
B三点的抛物线所表示的二
次函数的表达式；
(3)连接AB,
在(2)中的抛物线上求出点P,
使得S△ABP
=S△ABO
(点P不与点O重合)．
图1-Z-12
例3
[咸宁中考]某市某外资企业生产的一批产品上市后30天内全部售完,
该企业对这批产品上市后每天的销售情况进行了跟踪调查.
其中,
国内市场的日销售量y1
(万件)与时间t(t为整数,
单位：天)的部分对应值如下表所示,而国外市场的日销售量y2
(万件)与时间t(t为整数,
单位：天)的关系如图1-Z-13所示．
时间t(天)
0
5
10
15
20
25
30
日销售量y1
(万件)
0
25
40
45
40
25
0
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1
与t的变化规律,
写出y1
与t的函数表达式及自变量t的取值范围；
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2
(万件)与时间t(t为整数,
单位：天)所符合的函数表达式,
并写出相应自变量t的取值范围；
(3)设国内、外市场的日销售总量为y万件,
写出y与t的函数表达式,
并判断上市第几天国内、外市场的日销售总量最大,
并求出此时的最大值．
分析
(1)由表中数据易知y1
与t之间是二次函数关系.
设y1
=a(t-0)·(t-30),
再把另一组y1
,
t的对应值代入上式即可求出表达式.
(2)由函数图像可知y2
与t之间是分段的一次函数关系,
根据t的不同取值
范围,
有不同的函数表达式.
(3)本题考查的是分段函数的有关知识,
当0≤t＜20时,
y=y1
+y2
=
(t-20)2
+80,
求出y的最大值；当20≤t≤30时,
y=y1
+y2
=
(t-5)2
+125,
亦可求出y的最大值．
解：(1)由表中数据易知y1
与t之间是二次函数关系.
设y1
=a(t-0)(t-30),
再将t=5,
y1
=25代入,
得a=
,
∴y1
=
t(t-30).
将其余各组对应值代入均满足上式,
故y1
与t的函数表达式为y1
=
t(t-30)(t为整数,
0≤t≤30).
(2)由函数图像可知y2
与t之间是分段的一次函数关系.
由图像可知：0≤t＜20时,
y2
=2t；
当20≤t≤30时,
设y2
=kx+b,
将(20,
40),
(30,
0)代入可得
∴y2
=-4t+120,
∴y2
=
(3)当0≤t＜20时,
y=y1
+y2
=
t(t-30)+2t=80
(t-20)2
,
可知其对应的抛物线开口向下,
对称轴为直线t=20,
当0≤t<20时,
y随t的增大而增大,
∴y的最大值小于t=20时y的值80.
当20≤t≤30时,
y=y1
+y2
=
t(t-30)-4t+120=125
(t-5)2
,
可知其对应的抛物线开口向下,
对称轴为直线t=5,
当20≤t≤30时,
y随t的增大而减小,
∴y的最大值为t=20时y的值80.
故上市第20天,
国内、外市场的日销售总量最大,
最大值为80万件.
相关题3-1
某农户计划利用现有的一面墙(墙足够长)再修四面墙,
建造如图1-Z-14所示的长方体水池,培育不同品种的鱼苗．他已备足可以修高为1.5
m、长为18
m的墙的材料准备施工,
设图中与现有一面墙垂直的三面墙的长度都为x
m,
即AD=EF=BC=x
m.
(不考虑墙的厚度)
(1)若想水池的总容积为36
m
3
,
则x应等于多少？
(2)求水池的总容积V关于x的函数表达式,
并直接
写出x的取值范围；
(3)若想使水池的总容积V最大,
则x应为多少？最
大容积为多少？
相关题3-2
某商场经销一种商品,已知每件商品进价为40元,
现在每件售价为70元,
每星期可卖出500件,
该商场通过市场调查发现：若每件商品每涨价1元,
则每星期少卖出10件；若每件商品每降价1元,
则每星期多卖出m(m为正整数)件,
设调查价格后每星期的销售利润为W元.
(1)设该商品每件涨价x(x为正整数)元.
①若x=5,
则每星期可卖出　　　件,
每星期的销售利润为　　　元；
②当x为何值时,
W最大,W的最大值是多少？
相关题3-2
某商场经销一种商品,已知每件商品进价为40元,
现在每件售价为70元,
每星期可卖出500件,
该商场通过市场调查发现：若每件商品每涨价1元,
则每星期少卖出10件；若每件商品每降价1元,
则每星期多卖出m(m为正整数)件,
设调查价格后每星期的销售利润为W元.
(2)设该商品每件降价y(y为正整数)元,
①写出W与y的函数表达式,
并通过计算判断：当m=10时,
每星期销售利润能否达到(1)中W的最大值；
②若使y=10时,
每星期的销售利润W最大,
直接
写
出
W
的
最
大
值
为　　　　.
相关题3-2
某商场经销一种商品,已知每件商品进价为40元,
现在每件售价为70元,
每星期可卖出500件,
该商场通过市场调查发现：若每件商品每涨价1元,
则每星期少卖出10件；若每件商品每降价1元,
则每星期多卖出m(m为正整数)件,
设调查价格后每星期的销售利润为W元.
(3)若每件降价5元时每星期的销售利润不低于每件涨价15元时每星期的销售利润,
求m的取值范围.
解：(3)每件降价5元时销售利润W＝(70－40－5)(500＋5m)＝125m＋12
500.
每件涨价15元时的销售利润W＝(70－40＋15)(500－10×15)＝
15
750.
根据题意，得125m＋12500≥15
750，
解得m≥26.
答：m的取值范围是m≥26.
中考链接
母题1
(教材P15练习第1题)
写出下列二次函数的图像的对称轴、顶点坐标和开口方向：
(1)y=
(x-9)2
+7；(2)y=
(x+18)2
-13.
考点：二次函数图像的对称轴、顶点坐标、开口方向以及函数的增减性等.
考情：二次函数的图像与性质是中考必考内容,既可以填空题与选择题的形式出现,
也可以与其他知识点相结合以解答题的形式出现.
策略：一般是通过配方,
将函数表达式化为顶点式,
再根据二次函数的性质确定,
也可以运用顶点坐标公式计算.
链接1
[岳阳中考]抛物线y=3(x-2)2
+5的顶点坐标是(　　).
A．(-2,
5)
B．(-2,
-5)
C．(2,
5)
D．(2,
-5)
C
B
链接2
[益阳中考]已知二次函数y=ax2
+bx+c的图像如图1－
Z－15所示,
则下列选项正确的是(　　).
A．ac<0
B．b<0
C．b
2
-4ac<0
D．a+b+c<0
图1-Z-15
分析
由图可知,
抛物线开口向上,
∴a>0.
∵抛物线与y轴的交点在y轴正半轴,
∴c>0,
∴ac>0,选项A错误；
∵对称轴在y轴右侧,
∴a,
b异号,
故b<0,
选项B正确；
∵抛物线与x轴有两个不同的交点,
∴b2
-4ac>0,
选项C错误；
由图像可知,
当x=1时,
y>0,
∴a＋b＋c>0,
选项D错误.
故选B.
母题2
(教材P37复习题1第3题)
填空：
(1)抛物线y=3x2
先向左平移2个单位,
得到抛物线　　　；接着向上平移1个单位,
得到抛物线
.
(2)抛物线y=
x2
沿着x轴翻折并“复制”出来,
得到抛物线　　　；接着向右平移5个单位,
得到抛物线　　　；接着向下平移2个单位,
得到抛物线　　　.
考点：二次函数y=ax2
+bx+c(a≠0)与y=ax2
(a≠0)的图像间的平移关系.
考情：涉及二次函数图像间的平移问题,
一般以选择题、填空题的形式考查,
可正向考查,
也可逆向考查.
策略：解决二次函数图像间的平移问题,
首先将抛物线所表示的二次函数的表达式写成顶点式求得顶点坐标,
然后将顶点进行平移.
点的坐标平移规律：左右平移对横坐标进行加减运算(左减右加)；上下平移对纵坐标进行加减运算(上加下减).
利用这个规律可得到所求抛物线的顶点坐标,
进而求得平移后的抛物线所表示的二次函数的表达式.
链接3
[常德中考]将抛物线y=2x2
向右平移3个单位,
再向下平移5个单位,
得到的抛物线的函数表达式为(　　).
A．y=2(x-3)2
-5
B．y=2(x+3)2
+5
C．y=2(x-3)2
+5
D．y=2(x+3)2
-5
A
分析
抛物线y=2x
2
的顶点坐标为(0,
0),
点(0,0)向右平移3个单位,
再向下平移5个单位所得点的坐标为(3,
-5),
所以平移后得到的抛物线的函数表达式为y=2(x-3)2
-5.
③④
链接4
[岳阳中考]如图1－Z－16,
已知抛物线y=ax2
+bx+c与x轴交于A,
B两点,
顶点C的纵坐标为－2,
现将抛物线向右平移2个单位,
得到抛物线y=a1
x2
+b1
x+c1
,
则下列结论正确的是
　　　．(写出所有正确结论的序号)
①b＞0；
②a－b+c＜0；
③阴影部分的面积为4；
④若c=－1,
则b2
=4a．
图1－Z－16
分析
∵抛物线开口向上,
∴a＞0.
又∵对称轴为直线x=
＞0,
∴b＜0,
∴结论①不正确；
∵x=－1时,
y＞0,
∴a－b+c＞0,
∴结论②不正确；
由题易知阴影部分是平行四边形.
∵抛物线向右平移了2个单位,
∴平行四边形的底边长是2.
∵二次函数y=ax2
+bx+c的最小值是y=－2,
∴平行四边形的高是2,
∴阴影部分的面积是2×2=4,∴结论③正确；
∵
=-2,
c=－1,
∴b2
=4a,
∴结论④正确．综上,
正确的结论是③④.
链接5
[宁波中考]已知抛物线y=-
x2
+bx+c经过点(1,
0),
(
0,
)
.
(1)求抛物线的函数表达式；
(2)将抛物线y=-
x2
+bx+c平移,
使其顶点恰好落在原点,
请写出一种平移的方法及平移后的抛物线所表示的函数表达式.
解：
(1)把(1,
0)和
(
0,
)
代入y=-
x2
+bx+c,
-
+b+c=0,
b=-1,
得
解得
c=
,
c=
,
∴抛物线的函数表达式为y=-
x2
-x+
.
(2)∵y=-
x2
-x+
=-
(x+1)2
+2,
∴顶点坐标为(-1,
2),
∴将抛物线y=-
x2
-x+
平移,
使其顶点恰好落在原点的一种平移方法是：先向右平移1个单位,
再向下平移2个单位(平移方法不唯一),平移后的抛物线所表示的函数表达式为y=-
x2
.
母题3
(教材P28习题1.4第4题)
当t取什么值时,
抛物线y=5x2
+4tx+t2
-1与x轴有一个交点？
考点：二次函数与一元二次方程的关系.
考情：在中考中本知识点考查形式多样,
既有填空题、选择题,
也有与其他知识点相结合的解答题,
常常结合一元二次方程根的判别式考查.
策略：利用一元二次方程与二次函数的关系,
可以求出函数表达式中待定字母的值或取值范围：
Δ＞0
一元二次方程有两个不相等的实数根
二次函数图像与x轴有两个不同的交点；
Δ=0
一元二次方程有两个相等的实数根 二次函数图像与x轴有两个相同的交点(顶点在x轴上)；
Δ＜0
一元二次方程没有实数根
二次函数图像与x轴没有交点.
链接6
[永州中考]若抛物线y=x2
+2x+m-1与x轴有两个不同的交点,
则m的取值范围是(　　).
A．m＜2
B．m>2
C．0＜m≤2
D．m＜-2
A
分析
∵抛物线y=x2
+2x+m-1与x轴有两个不同的交点,
∴Δ=b2
-4ac>0,
即4-4m+4>0,
解得m<2.
故选A.
链接7
[南京中考]已知二次函数y＝2(x－1)·(x－m－3)(m为常数)．
(1)求证：不论m为何值,
该函数的图像与x轴总有公共点；
(2)当m取什么值时,
该函数的图像与y轴的交点在x轴的上方？
分析
(1)将y=0代入二次函数表达式中求出x的值,
进而即可证出：不论m为何值,
该函数的图像与x轴总有公共点；
(2)利用二次函数图像上点的坐标特征求出该函数的图像与y轴交点的纵坐标,
令其大于0即可求出结论.
解：
(1)证明：当y=0时,
可得方程2(x-1)(x-m-3)=0.
解得x1
=1,
x2
=m+3.
所以,
不论m为何值,
该函数的图像与x轴总有公共点.
(2)当x=0时,
y=2m+6,
即该函数的图像与y轴交点的纵坐标是2m+6.
当2m+6>0,
即m>-3时,
该函数的图像与y轴的交点在x轴的上方.
母题4
(教材P31例)
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元销售,
那么一个月内可售出180件.根据销售经验,
提高销售单价会导致销售量的下降,
即销售单价每上涨1元,
月销售量将相应减少10件.
当销售单价为多少元时,
该店能在一个月内获得最大利润？
考点：二次函数的实际应用.
考情：常与鲜明时事背景、地方特色、一次函数图像或二次函数图像相结合,
以解答题的形式出现.
策略：充分挖掘题中的等量关系,
然后将实际问题转化为数学问题,
运用配方法或公式法求二次函数的最值.
链接8
[福建中考]如图1－Z－17,
在足够大的空地上有一段长为a米的旧墙MN,
某人利用旧墙和木栏围成一个矩形菜园ABCD,
其中AD≤MN,
已知矩形菜园的一边靠墙,
另三边一共用了100米木栏．
(1)若a=20,
所围成的矩形菜园的面积为450平方米,
求所利用旧墙AD的长；
(2)求矩形菜园ABCD面积的最大值．
图1－Z－17
分析
(1)设AB=x米,
则BC=(100-2x)米,
利用矩形的面积公式得到x(100-2x)
=450,
解方程,
得x1
=5,
x2
=45,
然后计算100-2x与20进行比较即可得到AD
的长；
(2)设AD=x米,
利用矩形面积得到S=
x(100-x),
配方得到S=-
(x-50)2
+1250.
讨论：当a≥50时,
根据二次函数的性质得S的最大值为1250；
当0根据二次函数的性质得S的最大值为50a-
a2
.
解：
(1)设AB=x米,
则BC=(100-2x)米.
根据题意,
得x(100-2x)=450,
解得x1
=5,
x2
=45.
当x=5时,
100-2x=90>20,
不合题意,
舍去.
当x=45时,
100-2x=10.
答：所利用旧墙AD的长为10
米.
(2)设AD=x
米,
∴S=
x(100-x)=-
(x-50)2
+1250.
当a≥50时,
x=50时,
S的最大值为1250；
当00S随x的增大而增大,
此时当x=a时,
S的最大值为50a-
a2
.
综上所述,
当a≥50时,
矩形菜园ABCD面积的最大值为1250平方米；
当0矩形菜园ABCD面积的最大值为(
50a-
a2)
平方米.
链接9
[长沙中考]在长株潭建设两型社会的过程中,
为推进节能减排,
发展低碳经济,
我市某公司以25万元购得某项节能产品的生产技术后,
再投入100万元购买生产设备进行该产品的生产加工.
已知生产这种产品的成本价为每件20元.
经过市场调研发现,
该产品的销售单价定在25元/件到35元/件之间较为合理,
并且该产品的年销售量y(万件)与销售单价x(元/件)之间的函数表达式为
y=
(年获利=年销售收入-生产成本-投资成本)
(1)当销售单价定为28元/件时,
该产品的年销售量为多少万件？
(2)求该公司第一年的年获利W(万元)与销售单价x(元/件)之间的函数表达式,
并说明投资的第一年,
该公司是赢利还是亏损.
若赢利,
最大利润是多少？若亏损,
最小亏损是多少？
(3)第二年,
该公司决定给希望工程捐款Z万元,该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品,
就抽出1元钱作为捐款.
若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,
到第二年年底,
两年的总赢利不低于67.5万元,
请你确定此时销售单价的范围.
解：
(1)当x=28时,
y=40-28=12.
答：当销售单价定为28元/件时,
该产品的年销售量为12万件.
(2)①当25≤x≤30时,W=(40-x)(x-20)-25-100=-x2
+60x-925=-(x-30)2
-25,
故当x=30时,
W最大为-25,即公司最小亏损为25万元.
②当30＜x≤35时,
W=(25-0.5x)(x-20)-25-100=-0.5x2
+35x-625=-0.5(x-35)2
-12.5,
故当x=35时,
W最大为-12.5,
即公司最小亏损为12.5万元.
综上所述,
投资的第一年,
公司亏损,
最小亏损为12.5万元.
(3)设到第二年年底,
两年的总赢利为w万元.
①当25≤x≤30时,
w=(40-x)(x-20-1)-12.5-10=-x2
+61x-862.5,
令w=67.5,
则-x2
+61x-862.5=67.5,
化简得x
2
-61x+930=0,解得x1
=30,
x2
=31(舍去),
因此,
当两年的总赢利不低于67.5万元时,x=30.
②当30＜x≤35时,
w=(25-0.5x)(x-20-1)-12.5-10=-0.5x2
+35.5x-547.5,
令w=67.5,
则-0.5x2
+35.5x-547.5=67.5,
化简得x2
-71x+1230=0,解得x1
=30,
x2
=41(舍去),
此时,
当两年的总赢利不低于67.5万元时,30＜x≤35.
综上,
当30≤x≤35时,
两年的总赢利不低于67.5万元.
谢
谢
观
看！