1.1直角三角形的性质和判定(1)课件(19张ppt)
文档属性
| 名称 | 1.1直角三角形的性质和判定(1)课件(19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 20:35:41 | ||
图片预览





文档简介
(共19张PPT)
1.1 直角三角形的性质和判定
第1章 直角三角形
1.了解直角三角形两个锐角的关系.(重点)
学习目标
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
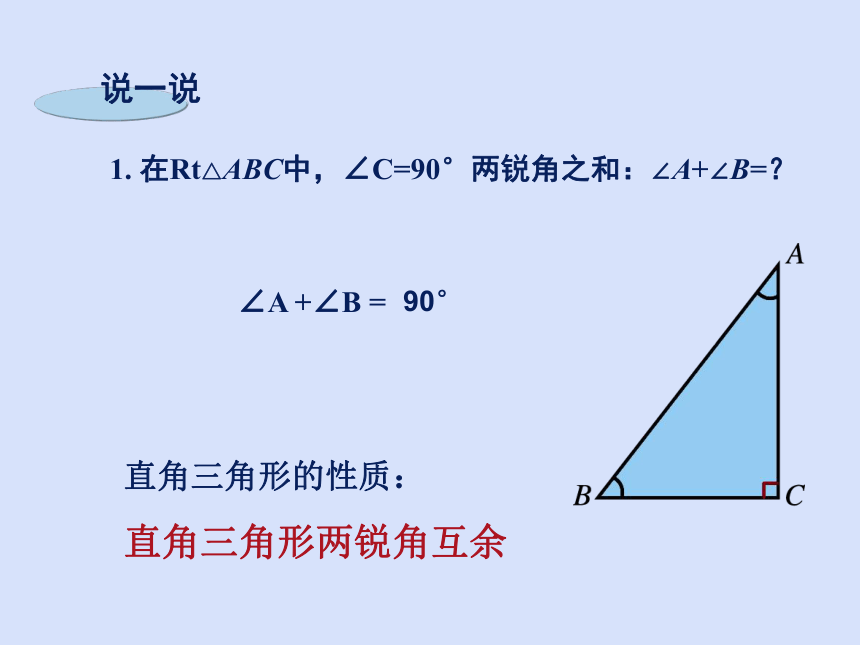
1. 在Rt△ABC中,∠C=90°两锐角之和:∠A+∠B=?
说一说
∠A +∠B =
90°
直角三角形的性质:
直角三角形两锐角互余
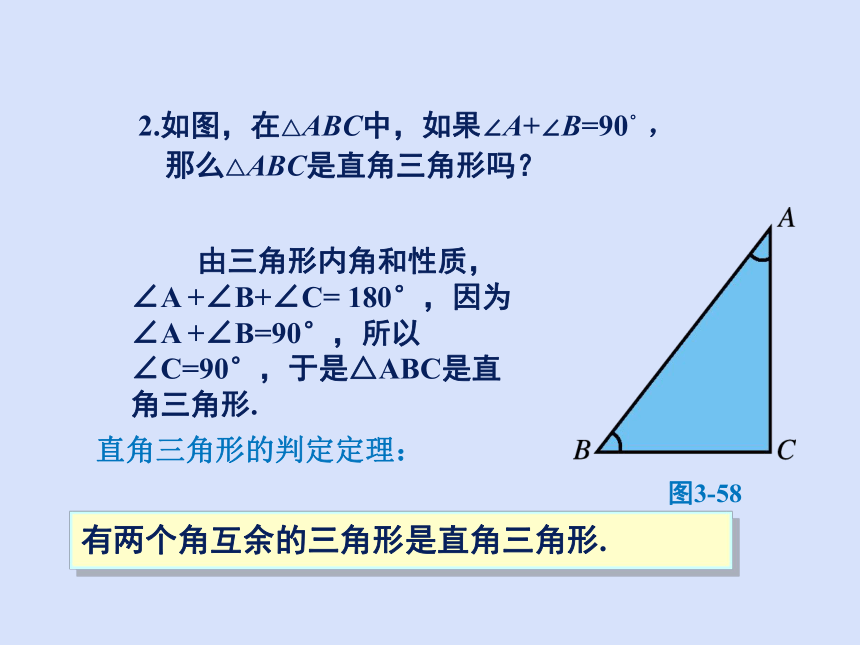
2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗?
图3-58
由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形.
直角三角形的判定定理:
画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。
探究
CD= ;
AD= ;
BD= ;
AB= ;
CD= AB
你们得到了什么结论?
结论
在直角三角形中,斜边上的中线等于斜边的一半.
直角三角形的性质定理:
是否任意一个Rt △ABC都有 成立呢?
图2
如图1,如果中线 ,即CD=AD,所以∠ACD=∠A。于是在图2中,过 Rt△ABC 的直角顶点 C 作射线 CD′交 AB 于 D′,使 ∠1 = ∠A,则有
(等角对等边)
图1
直角三角形两个角等于90°
又∵∠A +∠B = 90° ( )
∠1 +∠2 = 90°
∴ ∠B =∠2
∴ (等角对等边)
∴
∴ D′是斜边AB的中点
即CD′就是斜边AB的中线,从而CD′与CD重合,并且有
如图,在Rt△ABC 中,∠C=90°,D是AB的中点,连结CD,求证:
C
B
A
D
E
提示:延长CD,使得CD=DE,连结BE,
先证△ACD≌ △BED,然后证△ACB≌ △EBC,得AB=CE,最后说明
求证:在直角三角形中,斜边上的中线等于斜边的一半。
举
例
例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
如图,已知:CD是△ABC的AB边上的中线,且
求证: △ABC是直角三角形.
证明:
∵
∴ ∠1=∠A
等边对等角
∠2=∠B ( )
又 ∵ ∠A+∠B+∠ACB =180°(三角形 内角和的性质)
即∠A+∠B+∠1+∠2=180°
∴ 2(∠A+∠B)=180°
∴ ∠A+∠B =90°
∴ △ABC是直角三角形( )
有两个角互余的三角形是直角三角形
结论
三角形一边上的中线等于这条边的一半的
三角形是直角三角形.
直角三角形的判定定理:
例2:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
变式训练.已知,如图,BD、CE分别是△ABC的高,M、N分别是BC、DE的中点,分别连结ME,MD。
求证:MN⊥ED
变式训练:如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????;
(2)在Rt△ABC中,∠C=90度,∠A -∠B =30度,那么∠A=?????? ,∠B=?????? ;
(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.
(4)在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.
练习
小结与复习
1.本节课我们学习了哪些内容?
直角三角形的性质:
直角三角形的判定:
1:直角三角形两锐角互余;
2:在直角三角形中,斜边上的中线等于斜边的一半;
……
2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。
3:有两个角互余的三角形是直角三角形;
……
1、如图,在Rt△ABC中,∠ACB=90度,CD是斜边AB上的高,那么, 与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,与∠A相等的角有?????????.
C
A
B
D
作业:
2、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.求证:AB=AC
D
C
A
B
E
F
如图,已知,Rt△ABC中,∠ACB=90°,M是AB上的中点,CH⊥AB于H,CD平分∠ACB
(1)?? 求证:∠1=∠2
(2)?? 过点M作AB的垂直平分线交CD延长线于E, 求证:CM=EM
(3)?? △AEB是什么三角形?证明你的猜想
思考与探究:
1.1 直角三角形的性质和判定
第1章 直角三角形
1.了解直角三角形两个锐角的关系.(重点)
学习目标
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
1. 在Rt△ABC中,∠C=90°两锐角之和:∠A+∠B=?
说一说
∠A +∠B =
90°
直角三角形的性质:
直角三角形两锐角互余
2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗?
图3-58
由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形.
直角三角形的判定定理:
画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。
探究
CD= ;
AD= ;
BD= ;
AB= ;
CD= AB
你们得到了什么结论?
结论
在直角三角形中,斜边上的中线等于斜边的一半.
直角三角形的性质定理:
是否任意一个Rt △ABC都有 成立呢?
图2
如图1,如果中线 ,即CD=AD,所以∠ACD=∠A。于是在图2中,过 Rt△ABC 的直角顶点 C 作射线 CD′交 AB 于 D′,使 ∠1 = ∠A,则有
(等角对等边)
图1
直角三角形两个角等于90°
又∵∠A +∠B = 90° ( )
∠1 +∠2 = 90°
∴ ∠B =∠2
∴ (等角对等边)
∴
∴ D′是斜边AB的中点
即CD′就是斜边AB的中线,从而CD′与CD重合,并且有
如图,在Rt△ABC 中,∠C=90°,D是AB的中点,连结CD,求证:
C
B
A
D
E
提示:延长CD,使得CD=DE,连结BE,
先证△ACD≌ △BED,然后证△ACB≌ △EBC,得AB=CE,最后说明
求证:在直角三角形中,斜边上的中线等于斜边的一半。
举
例
例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
如图,已知:CD是△ABC的AB边上的中线,且
求证: △ABC是直角三角形.
证明:
∵
∴ ∠1=∠A
等边对等角
∠2=∠B ( )
又 ∵ ∠A+∠B+∠ACB =180°(三角形 内角和的性质)
即∠A+∠B+∠1+∠2=180°
∴ 2(∠A+∠B)=180°
∴ ∠A+∠B =90°
∴ △ABC是直角三角形( )
有两个角互余的三角形是直角三角形
结论
三角形一边上的中线等于这条边的一半的
三角形是直角三角形.
直角三角形的判定定理:
例2:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
变式训练.已知,如图,BD、CE分别是△ABC的高,M、N分别是BC、DE的中点,分别连结ME,MD。
求证:MN⊥ED
变式训练:如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????;
(2)在Rt△ABC中,∠C=90度,∠A -∠B =30度,那么∠A=?????? ,∠B=?????? ;
(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.
(4)在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.
练习
小结与复习
1.本节课我们学习了哪些内容?
直角三角形的性质:
直角三角形的判定:
1:直角三角形两锐角互余;
2:在直角三角形中,斜边上的中线等于斜边的一半;
……
2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。
3:有两个角互余的三角形是直角三角形;
……
1、如图,在Rt△ABC中,∠ACB=90度,CD是斜边AB上的高,那么, 与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,与∠A相等的角有?????????.
C
A
B
D
作业:
2、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.求证:AB=AC
D
C
A
B
E
F
如图,已知,Rt△ABC中,∠ACB=90°,M是AB上的中点,CH⊥AB于H,CD平分∠ACB
(1)?? 求证:∠1=∠2
(2)?? 过点M作AB的垂直平分线交CD延长线于E, 求证:CM=EM
(3)?? △AEB是什么三角形?证明你的猜想
思考与探究:
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
