人教版数学九下28.2 解直角三角形及其应用同步习题(带答案)
文档属性
| 名称 | 人教版数学九下28.2 解直角三角形及其应用同步习题(带答案) |  | |
| 格式 | zip | ||
| 文件大小 | 788.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 22:54:04 | ||
图片预览




文档简介
28.2 解直角三角形及其应用同步习题
一.选择题(共10小题)
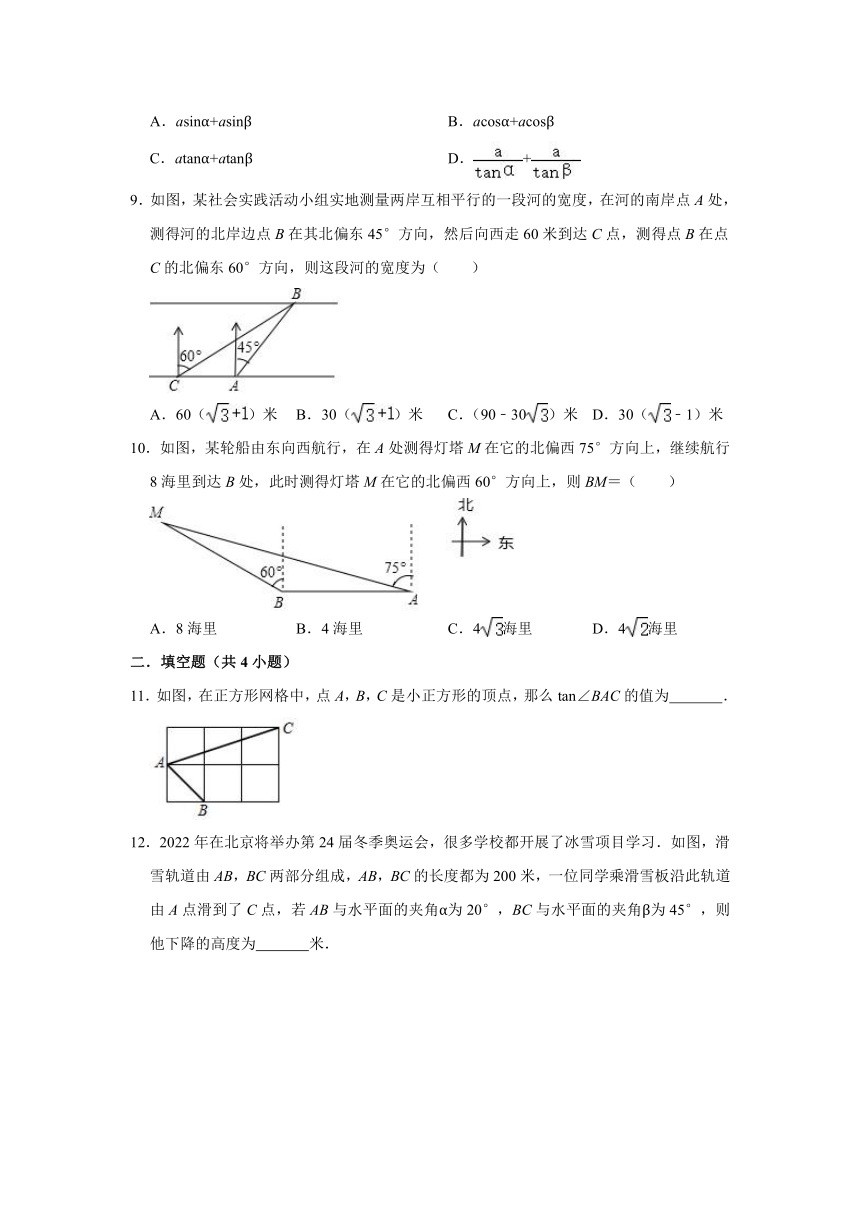
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴y的夹角α的余切值是( )
A. B. C. D.
2.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为( )
A. B. C. D.
3.如图,一根电线杆PO垂直于地面,并用两根拉线PA,PB固定,量得∠PAO=α,∠PBO=β,则拉线PA,PB的长度之比=( )
A. B. C. D.
4.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
5.某人沿着坡度为1:2.4的斜坡向上前进了130m,那么他的高度上升了( )
A.50m B.100m C.120m D.130m
6.如图是一斜坡的横截面,某人沿斜坡从M出发,走了13米到达N处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是( )
A.1:5 B.12:13 C.5:13 D.5:12
7.直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )
A.俯角67°方向 B.俯角23°方向
C.仰角67°方向 D.仰角23°方向
8.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
9.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )
A.60()米 B.30()米 C.(90﹣30)米 D.30(﹣1)米
10.如图,某轮船由东向西航行,在A处测得灯塔M在它的北偏西75°方向上,继续航行8海里到达B处,此时测得灯塔M在它的北偏西60°方向上,则BM=( )
A.8海里 B.4海里 C.4海里 D.4海里
二.填空题(共4小题)
11.如图,在正方形网格中,点A,B,C是小正方形的顶点,那么tan∠BAC的值为 .
12.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为 米.
13.小明沿着坡度i=1:2.5的斜坡前行了29米,那么他上升的高度是 米.
14.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= 米(结果保留根号).
三.解答题(共9小题)
15.在△ABC中,AB=6,BC=4,∠B为锐角且.
(1)求∠B的度数;
(2)求△ABC的面积;
(3)求tanC.
16.如图,Rt△ABC中,∠C=90°,AC=2,BC=6,解这个直角三角形.
17.如图,胡同左右两侧是竖直的墙,一架3米长的梯子斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,问:胡同左侧的通道拓宽了多少米(保留根号)?
18.图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
19.水务部门为加强防汛工作,决定对马边河上某电站大坝进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为20米,∠B=60°,背水面DC的长度为20米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号).
20.某仓储中心有一个坡度为i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE=2.5米,高EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH.
21.如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈,cos37°≈,tan37°≈).
22.水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:
如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
23.如图,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市150km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,120km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:≈1.732)
参考答案
一.选择题(共10小题)
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴y的夹角α的余切值是( )
A. B. C. D.
【解答】解:过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
在Rt△OAB中,cot∠AOB=cotα==,
故选:B.
2.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为( )
A. B. C. D.
【解答】解:如图所示:
由勾股定理得:AC==5,
∴tanA==;
故选:D.
3.如图,一根电线杆PO垂直于地面,并用两根拉线PA,PB固定,量得∠PAO=α,∠PBO=β,则拉线PA,PB的长度之比=( )
A. B. C. D.
【解答】解:如图,在直角△PAO中,∠POA=90°,∠PAO=α,则PA=.
如图,在直角△PBO中,∠POB=90°,∠PBO=β,则PA=.
所以==.
故选:D.
4.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
【解答】解:如图,延长BA、FE,交于点D,
∵AB⊥BC,EF∥BC,
∴BD⊥DF,即∠ADE=90°,
∵∠AEF=143°,
∴∠AED=37°,
在Rt△ADE中,
∵sin∠AED=,AE=1.2米,
∴AD=AEsin∠AED=1.2×sin37°≈0.72(米),
则BD=AB+AD=1.18+0.72=1.9(米),
故选:A.
5.某人沿着坡度为1:2.4的斜坡向上前进了130m,那么他的高度上升了( )
A.50m B.100m C.120m D.130m
【解答】解:如图,
根据题意知AB=130米,tanB==1:2.4,
设AC=x,则BC=2.4x,
则x2+(2.4x)2=1302,
解得x=50或x=﹣50(负值舍去),
即他的高度上升了50m,
故选:A.
6.如图是一斜坡的横截面,某人沿斜坡从M出发,走了13米到达N处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是( )
A.1:5 B.12:13 C.5:13 D.5:12
【解答】解:过点N作HG⊥地面AB于G再作MH⊥NG于H,
由题意得,MN=13,NH=5,
由勾股定理得,MH===12,
∴该斜坡的坡度为5:12,
故选:D.
7.直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )
A.俯角67°方向 B.俯角23°方向
C.仰角67°方向 D.仰角23°方向
【解答】解:∵BC⊥AB,∠BCA=67°,
∴∠BAC=90°﹣∠BCA=23°,
从低处A处看高处C处,那么点C在点A的仰角23°方向;
故选:D.
8.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
【解答】解:∵在Rt△ABC中,
BC=AB?tanα=atanα,
在Rt△ABD中,
BD=AB?tanβ=atanβ,
∴CD=BC+BD=atanα+atanβ.
故选:C.
9.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )
A.60()米 B.30()米 C.(90﹣30)米 D.30(﹣1)米
【解答】解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x==30(),
答:这段河的宽约为30()米.
故选:B.
10.如图,某轮船由东向西航行,在A处测得灯塔M在它的北偏西75°方向上,继续航行8海里到达B处,此时测得灯塔M在它的北偏西60°方向上,则BM=( )
A.8海里 B.4海里 C.4海里 D.4海里
【解答】解:由题意得,∠BAM=90°﹣75°=15°,
∴∠M=180°﹣90°﹣60°﹣15°=15°,
∴∠BAM=∠M,
∴BM=AB=8(海里),
故选:A.
二.填空题(共4小题)
11.如图,在正方形网格中,点A,B,C是小正方形的顶点,那么tan∠BAC的值为 2 .
【解答】解:连接BC,则AB⊥BC,在Rt△ABC中,
AB==,BC==2,
∴tan∠BAC===2,
故答案为:2.
12.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为 210 米.
【解答】解:过点A作AE⊥BD于点E,过点B作BG⊥CF于点G,
在Rt△ABE中,
∴sinα=,
∴AE=AB×sin20°≈68,
在Rt△BCG中,
∴sinβ=,
∴BG=BC×sin45°≈142,
∴他下降的高度为:AE+BG=210,
故答案为:210
13.小明沿着坡度i=1:2.5的斜坡前行了29米,那么他上升的高度是 2 米.
【解答】解:设小明上升的高度为x米,
∵坡度i=1:2.5,
∴小明前行的水平宽度为2.5x米,
由勾股定理得,x2+(2.5x)2=292,
解得,x=2,
故答案为:2.
14.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= (100+100) 米(结果保留根号).
【解答】解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD?sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:(100+100).
三.解答题(共9小题)
15.在△ABC中,AB=6,BC=4,∠B为锐角且.
(1)求∠B的度数;
(2)求△ABC的面积;
(3)求tanC.
【解答】解:(1)∵∠B为锐角且,
∴∠B=60°;
(2)作AD⊥BC于D,如图所示:
∵∠B=60°,
∴∠BAD=90°﹣60°=30°,
∴BD=AB=3,
∴AD=BD=3,
∴△ABC的面积=BC×AD=×4×3=6;
(3)∵BC=4,BD=3,
∴CD=BC﹣BD=1,
∴tanC===3.
16.如图,Rt△ABC中,∠C=90°,AC=2,BC=6,解这个直角三角形.
【解答】解:Rt△ABC中,∠C=90°,AC=2,BC=6,
由勾股定理得,AB==4,
∵tanB===,
∴∠B=30°,
∴∠A=90°﹣30°=60°,
17.如图,胡同左右两侧是竖直的墙,一架3米长的梯子斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,问:胡同左侧的通道拓宽了多少米(保留根号)?
【解答】解:在Rt△BCE中,∵BC=3,∠BEC=90°,∠BCE=45°,
∴BE=CE=BC?cos45°=3×=3,
在Rt△BDE中,DE=BE?tan30°=,
∴CD=CE﹣DE=3﹣,
答:胡同左侧的通道拓宽了(3﹣)米.
18.图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
【解答】解:过B作BG⊥OM于G,
过C′作C′H⊥BG于H,延长D′A交BG于E,
则C′H=D′E,HE=C′D′=8,
设AE=x,
∴C′H=D′E=16+x,
∵∠BC′H=45°,
∴BH=C′H=16+x,
∴BE=16+x+8=24+x,
∵∠BAO=160°,
∴∠BAE=70°,
∴tan70°===,
解得:x=13.5,
∴BE=37.5,
∴BG=BE+EG=BE+AO=37.5+7=44.5≈45cm,
答:B到水平桌面OM的距离为45cm.
19.水务部门为加强防汛工作,决定对马边河上某电站大坝进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为20米,∠B=60°,背水面DC的长度为20米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号).
【解答】解:(1)分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
在Rt△ABF中,AB=20米,∠B=60°,
sin∠B=,
∴AF=20×=10,
DG=10.
∴S△DCE=×CE?DG=5×10=25,
需要填方:100×25=2500(立方米);
(2)在直角三角形DGC中,DC=20,
∴GC===30,
∴GE=GC+CE=35,
坡度i===.
答:(1)需要土石方2500立方米.
(2)背水坡坡度为.
20.某仓储中心有一个坡度为i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE=2.5米,高EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH.
【解答】解:(1)∵坡度为i=1:2,AC=4m,
∴BC=4×2=8m.
∴AB===(米);
(2)∵∠DGM=∠BHM,∠DMG=∠BMH,
∴∠GDM=∠HBM,
∴,
∵DG=EF=2m,
∴GM=1m,
∴DM=,BM=BF+FM=3.5+(2.5﹣1)=5m,
设MH=xm,则BH=2xm,
∴x2+(2x)2=52,
∴x=m,
∴DH==m.
21.如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈,cos37°≈,tan37°≈).
【解答】解:过C作CF⊥AM于F,过C作CH⊥AD于H,则四边形AHCF是矩形,所以AF=CH,CF=AH.
在Rt△BCF中,BC=1,∠CBF=37°.
BF=BCcos37°=0.8,CF=BCsin37°=0.6,
在Rt△BAE中,∠BEA=53°,所以AE=AB,
在Rt△CDH中,∠CDH=45°,
∴CH=DH=FA=0.8+AB,
∴AD=AH+DH=0.6+0.8+AB=1.4+AB,
∵AD=AE+DE=AB+2.4,
∴1.4+AB=AB+2.4,
AB=4,
答:匾额悬挂的高度是4米.
22.水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:
如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
【解答】解:由题意得,∠ABD=90°,∠D=20°,∠ACB=31°,CD=13,
在Rt△ABD中,∵tan∠D=,
∴BD==,
在Rt△ABC中,∵tan∠ACB=,
∴BC==,
∵CD=BD﹣BC,
∴13=,
解得AB≈11.7米.
答:水城门AB的高为11.7米.
23.如图,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市150km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,120km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:≈1.732)
【解答】解:计划修建的这条高速铁路穿越保护区,
理由如下:作PH⊥AC于H,
由题意得,∠PBH=60°,∠PAH=30°,
∴∠APB=30°,
∴∠BAP=∠BPA,
∴PB=AB=150,
在Rt△PBH中,sin∠PBH=,
∴PH=PB?sin∠PBH=75≈129.9,
129.9>120,
∴计划修建的这条高速铁路不会穿越保护区.
