2020春北师大版七下数学2.3平行线的性质同步练习(含解析)
文档属性
| 名称 | 2020春北师大版七下数学2.3平行线的性质同步练习(含解析) | 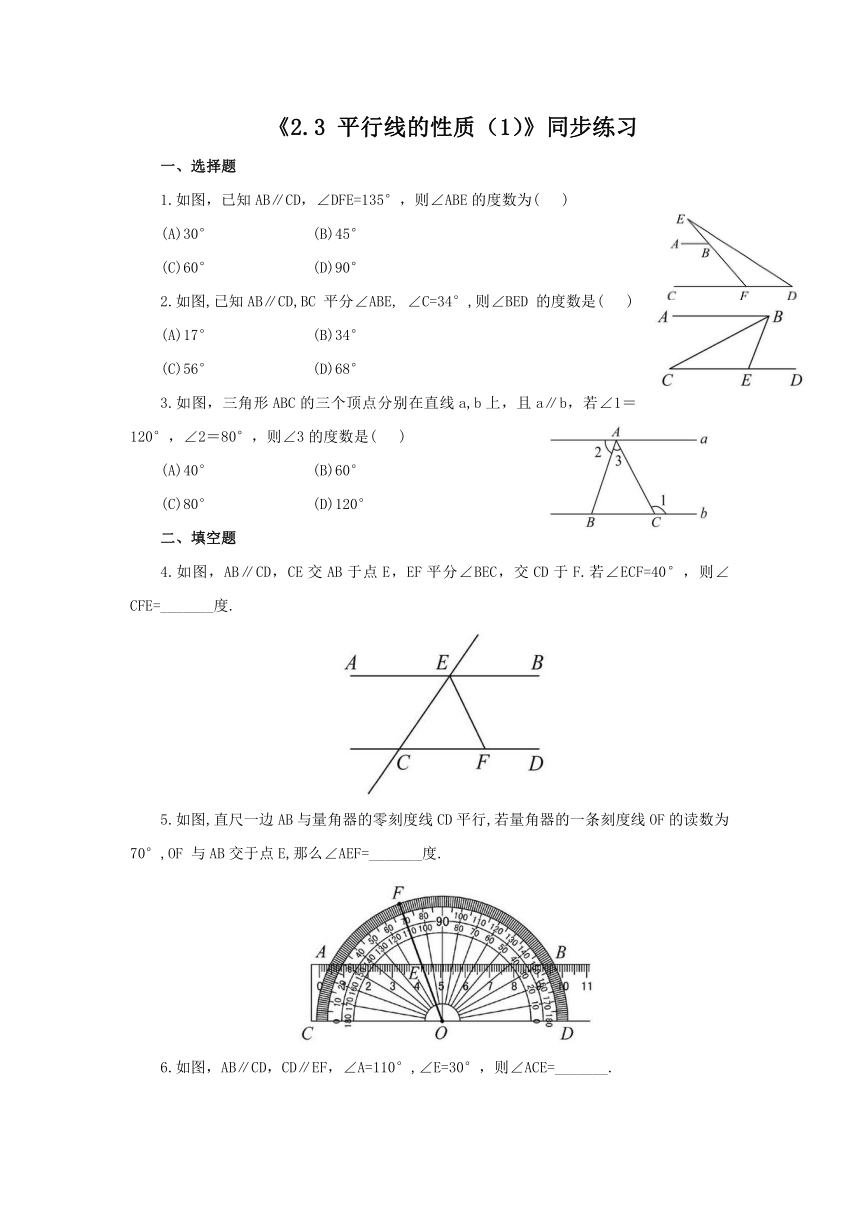 | |
| 格式 | zip | ||
| 文件大小 | 307.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 21:01:57 | ||
图片预览


文档简介
《2.3 平行线的性质(1)》同步练习
一、选择题
1.如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
(A)30° (B)45°
(C)60° (D)90°
2.如图,已知AB∥CD,BC 平分∠ABE, ∠C=34°,则∠BED 的度数是( )
(A)17° (B)34°
(C)56° (D)68°
3.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
(A)40° (B)60°
(C)80° (D)120°
二、填空题
4.如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=_______度.
5.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF 与AB交于点E,那么∠AEF=_______度.
6.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE=_______.
三、解答题
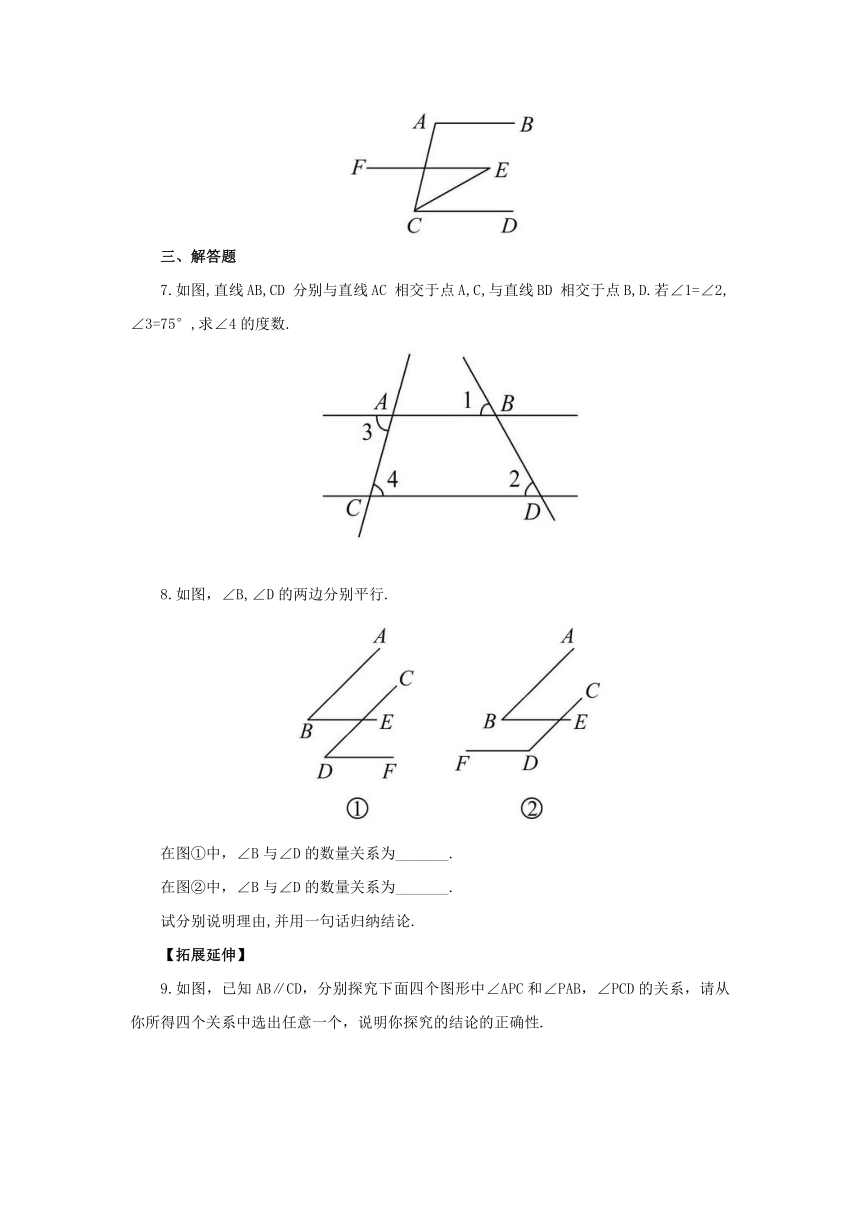
7.如图,直线AB,CD 分别与直线AC 相交于点A,C,与直线BD 相交于点B,D.若∠1=∠2, ∠3=75°,求∠4的度数.
8.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为_______.
在图②中,∠B与∠D的数量关系为_______.
试分别说明理由,并用一句话归纳结论.
【拓展延伸】
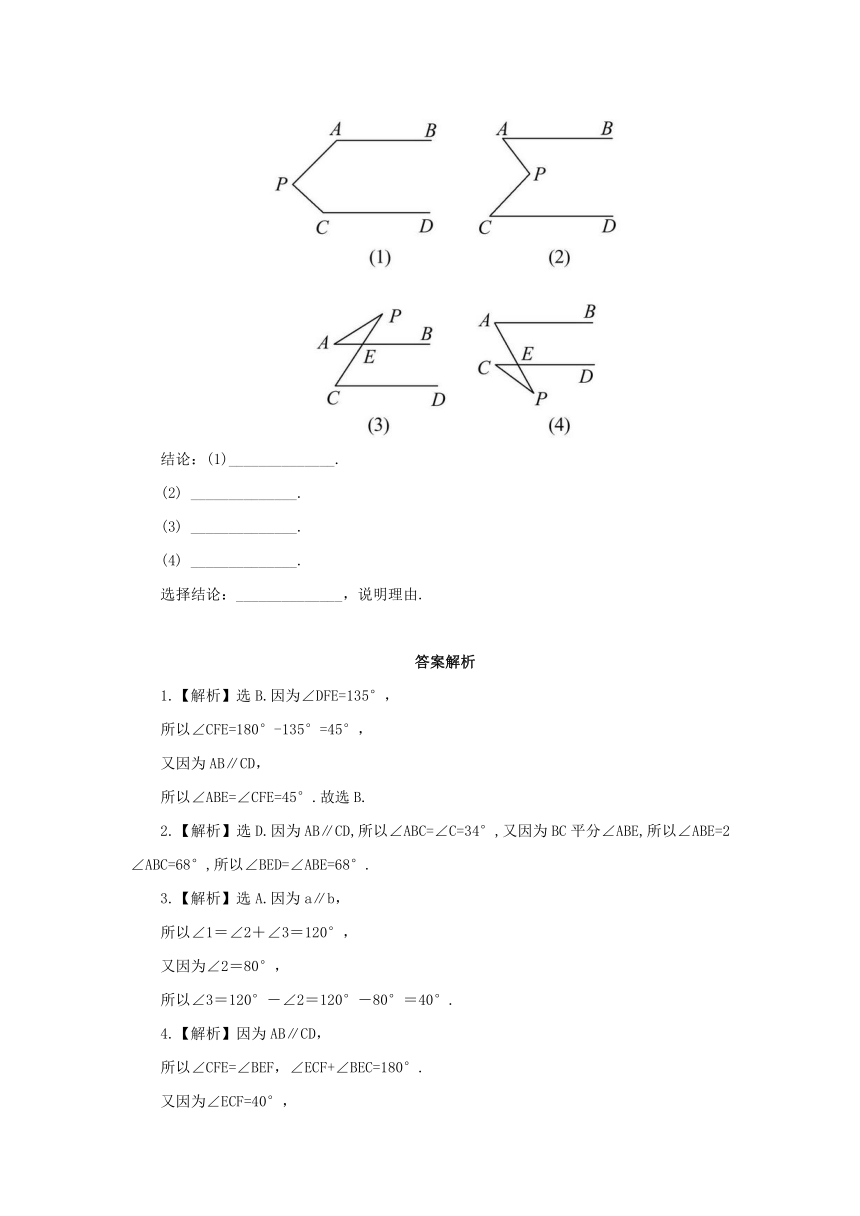
9.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1)______________.
(2) ______________.
(3) ______________.
(4) ______________.
选择结论:______________,说明理由.
答案解析
1.【解析】选B.因为∠DFE=135°,
所以∠CFE=180°-135°=45°,
又因为AB∥CD,
所以∠ABE=∠CFE=45°.故选B.
2.【解析】选D.因为AB∥CD,所以∠ABC=∠C=34°,又因为BC平分∠ABE,所以∠ABE=2∠ABC=68°,所以∠BED=∠ABE=68°.
3.【解析】选A.因为a∥b,
所以∠1=∠2+∠3=120°,
又因为∠2=80°,
所以∠3=120°-∠2=120°-80°=40°.
4.【解析】因为AB∥CD,
所以∠CFE=∠BEF,∠ECF+∠BEC=180°.
又因为∠ECF=40°,
所以∠BEC=140°.
因为EF平分∠BEC,
所以∠BEF=∠BEC=70°.
所以∠CFE=70°.
答案:70
5.【解析】直尺的对边互相平行,∠COF与∠AEF是同位角,又∠COF=70°,根据两直线平行,同位角相等,得∠AEF=70°.
答案:70
6.【解析】因为AB∥CD,∠A=110°,
所以∠ACD=180°-∠A=180°-110°=70°,
因为CD∥EF,∠E=30°,
所以∠ECD=∠E=30°,
所以∠ACE=∠ACD-∠ECD=70°-30°=40°.
答案:40°
7.【解析】因为∠1=∠2,
所以AB∥CD.
所以∠3=∠4.
因为∠3=75°,
所以∠4=75°.
8.【解析】图①中∠B与∠D相等.理由:
如图(1),因为BE∥DF,
所以∠CME=∠D,
因为AB∥DC,
所以∠B=∠CME,
所以∠B=∠D.
图②中∠B与∠D互补.理由:
如图(2),因为BE∥DF,
所以∠BND+∠D=180°,
因为AB∥DC,
所以∠B=∠BND,
所以∠B+∠D=180°.
结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
9.【解析】结论:(1)∠PAB+∠APC+∠PCD=360°
(2)∠APC =∠PAB+∠PCD
(3)∠APC =∠PCD-∠PAB
(4)∠APC =∠PAB-∠PCD
选择结论: 答案不惟一,
理由:(1)过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB+∠APQ=180°;由PQ∥CD得∠PCD+∠CPQ=180°,所以∠PAB+∠APQ+∠PCD+
∠CPQ=360°,即∠PAB+∠APC+∠PCD=360°.
(2)过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB=∠APQ;由PQ∥CD得∠PCD=∠CPQ,所以∠APC =∠PAB+∠PCD.
(3)因为AB∥CD,所以∠PEB=∠PCD,又因为∠AEP+∠APC+∠PAB=180°,∠PEB+∠AEP=180°,所以∠APC+∠PAB=∠PCD,
即∠APC =∠PCD-∠PAB.
(4) 因为AB∥CD,所以∠PED=∠PAB,又因为∠CEP+∠APC+∠DCP=180°,
∠PED+∠CEP=180°,所以∠APC+∠PCD=∠PAB,
即∠APC =∠PAB-∠PCD.
《2.3 平行线的性质(2)》同步练习
一、选择题
1.如图,AB∥ED,∠ECF=70°,则∠BAF的度数是( )
(A)130° (B)110°
(C) 70° (D)20°
2.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(A)30° (B)25° (C)20° (D)15°
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
(A)先向左转130°,再向左转50°
(B)先向左转50°,再向右转50°
(C)先向左转50°,再向右转40°
(D)先向左转50°,再向左转40°
二、填空题
4.如图,直线a∥b,∠1=130°,∠2=70°,则∠3的度数是______.
5.如图,已知∠1=∠2=∠3=59°,则∠4=______.
6.如图,将平行四边形ABCD的一边BC延长至E,若∠A=
110°,则∠1=______.
三、解答题
7.如图,AB∥CD,AD∥BC,∠B和∠D相等吗?为什么?
8.如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.
【拓展延伸】
9.如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的关系,并说明理由.
答案解析
1.【解析】选B.因为∠FCD与∠ECF互为补角,
所以∠FCD=180°-70°=110°,
又因为AB∥ED,
所以∠BAF=∠FCD=110°.
2.【解析】选B.因为a∥b,∠1=20°,所以∠3=∠1=20°,所以∠2=45°-
20°=25°.
3.【解析】选B.先向左转a°,再向右转b°形成的两个角是同位角关系,因为两次拐弯后,仍在原来的方向平行行驶,即两直线平行,所以a°=b°,故选B.
4.【解析】由两直线平行,同旁内角互补和对顶角相等得∠3=180°-(180°-∠1+∠2)=60°.
答案:60°
5.【解析】因为∠1=∠3,所以AB∥CD,
因为∠2=59°,
所以∠AOG=180°-∠2=121°,
所以∠4=121°.
答案:121°
6.【解析】因为平行四边形对边平行,所以AD∥BC,AB∥CD.又因为∠A=110°,根据平行线的特征:两直线平行,同旁内角互补,同位角相等,所以∠1=∠B=
180°-∠A=70°.
答案:70°
7.【解析】∠B和∠D相等.
因为AB∥CD,AD∥BC(已知),
所以∠A+∠D=180°,∠A+∠B=180°(两直线平行,同旁内角互补),
所以∠B=∠D(同角的补角相等).
8.【解析】因为AD∥BC,∠2=40°,
所以∠ADB=∠2=40°,
又因为∠1=78°,
所以∠ADC=∠ADB+∠1=40°+78°=118°.
9.【解析】∠AED=∠ACB.
理由如下:
因为∠1=∠DFG(对顶角相等),
又因为∠1+∠2=180°(已知),
所以∠DFG+∠2=180°(等量代换),
所以AB∥EG(同旁内角互补,两直线平行).
所以∠B=∠EGC(两直线平行,同位角相等),
又因为∠3=∠B(已知),
所以∠3=∠EGC(等量代换),
所以DE∥BC(内错角相等,两直线平行),
所以∠AED=∠ACB(两直线平行,同位角相等).
一、选择题
1.如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
(A)30° (B)45°
(C)60° (D)90°
2.如图,已知AB∥CD,BC 平分∠ABE, ∠C=34°,则∠BED 的度数是( )
(A)17° (B)34°
(C)56° (D)68°
3.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
(A)40° (B)60°
(C)80° (D)120°
二、填空题
4.如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=_______度.
5.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF 与AB交于点E,那么∠AEF=_______度.
6.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE=_______.
三、解答题
7.如图,直线AB,CD 分别与直线AC 相交于点A,C,与直线BD 相交于点B,D.若∠1=∠2, ∠3=75°,求∠4的度数.
8.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为_______.
在图②中,∠B与∠D的数量关系为_______.
试分别说明理由,并用一句话归纳结论.
【拓展延伸】
9.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1)______________.
(2) ______________.
(3) ______________.
(4) ______________.
选择结论:______________,说明理由.
答案解析
1.【解析】选B.因为∠DFE=135°,
所以∠CFE=180°-135°=45°,
又因为AB∥CD,
所以∠ABE=∠CFE=45°.故选B.
2.【解析】选D.因为AB∥CD,所以∠ABC=∠C=34°,又因为BC平分∠ABE,所以∠ABE=2∠ABC=68°,所以∠BED=∠ABE=68°.
3.【解析】选A.因为a∥b,
所以∠1=∠2+∠3=120°,
又因为∠2=80°,
所以∠3=120°-∠2=120°-80°=40°.
4.【解析】因为AB∥CD,
所以∠CFE=∠BEF,∠ECF+∠BEC=180°.
又因为∠ECF=40°,
所以∠BEC=140°.
因为EF平分∠BEC,
所以∠BEF=∠BEC=70°.
所以∠CFE=70°.
答案:70
5.【解析】直尺的对边互相平行,∠COF与∠AEF是同位角,又∠COF=70°,根据两直线平行,同位角相等,得∠AEF=70°.
答案:70
6.【解析】因为AB∥CD,∠A=110°,
所以∠ACD=180°-∠A=180°-110°=70°,
因为CD∥EF,∠E=30°,
所以∠ECD=∠E=30°,
所以∠ACE=∠ACD-∠ECD=70°-30°=40°.
答案:40°
7.【解析】因为∠1=∠2,
所以AB∥CD.
所以∠3=∠4.
因为∠3=75°,
所以∠4=75°.
8.【解析】图①中∠B与∠D相等.理由:
如图(1),因为BE∥DF,
所以∠CME=∠D,
因为AB∥DC,
所以∠B=∠CME,
所以∠B=∠D.
图②中∠B与∠D互补.理由:
如图(2),因为BE∥DF,
所以∠BND+∠D=180°,
因为AB∥DC,
所以∠B=∠BND,
所以∠B+∠D=180°.
结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
9.【解析】结论:(1)∠PAB+∠APC+∠PCD=360°
(2)∠APC =∠PAB+∠PCD
(3)∠APC =∠PCD-∠PAB
(4)∠APC =∠PAB-∠PCD
选择结论: 答案不惟一,
理由:(1)过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB+∠APQ=180°;由PQ∥CD得∠PCD+∠CPQ=180°,所以∠PAB+∠APQ+∠PCD+
∠CPQ=360°,即∠PAB+∠APC+∠PCD=360°.
(2)过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB=∠APQ;由PQ∥CD得∠PCD=∠CPQ,所以∠APC =∠PAB+∠PCD.
(3)因为AB∥CD,所以∠PEB=∠PCD,又因为∠AEP+∠APC+∠PAB=180°,∠PEB+∠AEP=180°,所以∠APC+∠PAB=∠PCD,
即∠APC =∠PCD-∠PAB.
(4) 因为AB∥CD,所以∠PED=∠PAB,又因为∠CEP+∠APC+∠DCP=180°,
∠PED+∠CEP=180°,所以∠APC+∠PCD=∠PAB,
即∠APC =∠PAB-∠PCD.
《2.3 平行线的性质(2)》同步练习
一、选择题
1.如图,AB∥ED,∠ECF=70°,则∠BAF的度数是( )
(A)130° (B)110°
(C) 70° (D)20°
2.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(A)30° (B)25° (C)20° (D)15°
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
(A)先向左转130°,再向左转50°
(B)先向左转50°,再向右转50°
(C)先向左转50°,再向右转40°
(D)先向左转50°,再向左转40°
二、填空题
4.如图,直线a∥b,∠1=130°,∠2=70°,则∠3的度数是______.
5.如图,已知∠1=∠2=∠3=59°,则∠4=______.
6.如图,将平行四边形ABCD的一边BC延长至E,若∠A=
110°,则∠1=______.
三、解答题
7.如图,AB∥CD,AD∥BC,∠B和∠D相等吗?为什么?
8.如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.
【拓展延伸】
9.如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的关系,并说明理由.
答案解析
1.【解析】选B.因为∠FCD与∠ECF互为补角,
所以∠FCD=180°-70°=110°,
又因为AB∥ED,
所以∠BAF=∠FCD=110°.
2.【解析】选B.因为a∥b,∠1=20°,所以∠3=∠1=20°,所以∠2=45°-
20°=25°.
3.【解析】选B.先向左转a°,再向右转b°形成的两个角是同位角关系,因为两次拐弯后,仍在原来的方向平行行驶,即两直线平行,所以a°=b°,故选B.
4.【解析】由两直线平行,同旁内角互补和对顶角相等得∠3=180°-(180°-∠1+∠2)=60°.
答案:60°
5.【解析】因为∠1=∠3,所以AB∥CD,
因为∠2=59°,
所以∠AOG=180°-∠2=121°,
所以∠4=121°.
答案:121°
6.【解析】因为平行四边形对边平行,所以AD∥BC,AB∥CD.又因为∠A=110°,根据平行线的特征:两直线平行,同旁内角互补,同位角相等,所以∠1=∠B=
180°-∠A=70°.
答案:70°
7.【解析】∠B和∠D相等.
因为AB∥CD,AD∥BC(已知),
所以∠A+∠D=180°,∠A+∠B=180°(两直线平行,同旁内角互补),
所以∠B=∠D(同角的补角相等).
8.【解析】因为AD∥BC,∠2=40°,
所以∠ADB=∠2=40°,
又因为∠1=78°,
所以∠ADC=∠ADB+∠1=40°+78°=118°.
9.【解析】∠AED=∠ACB.
理由如下:
因为∠1=∠DFG(对顶角相等),
又因为∠1+∠2=180°(已知),
所以∠DFG+∠2=180°(等量代换),
所以AB∥EG(同旁内角互补,两直线平行).
所以∠B=∠EGC(两直线平行,同位角相等),
又因为∠3=∠B(已知),
所以∠3=∠EGC(等量代换),
所以DE∥BC(内错角相等,两直线平行),
所以∠AED=∠ACB(两直线平行,同位角相等).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
