沪教版高中数学高一第二学期第四章T同步《对数函数》教案
文档属性
| 名称 | 沪教版高中数学高一第二学期第四章T同步《对数函数》教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 643.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 11:46:54 | ||
图片预览

文档简介
同步 对数函数 ★★
情境引入 .10min.
我们研究指数函数时,曾讨论过细胞分裂问题,某种细胞分裂时,由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂成次后,得到细胞个数是分裂次数的函数,这个函数可以用指数函数 表示.
反过来,1个细胞经过多少次分裂,大约可以等于1万个、10万个……细胞?已知细胞个数,如何求分裂次数?得到怎样一个新的函数?
1 2 4
根据对数的定义,这个函数可以写成对数的形式就是
如果用表示自变量,用表示函数,这个函数就是
由反函数的概念,可知函数与指数函数互为反函数.
对数函数:一般地,函数叫做对数函数,其中是自变量,函数的定义域是.
一般地,函数就是指函数的反函数,因为得值域是,所以,函数的定义域是.
问题1:当且时,比较函数与函数,它们的定义域和值域有什么关系?
答:函数的定义域、值域分别是函数的值域和定义域.
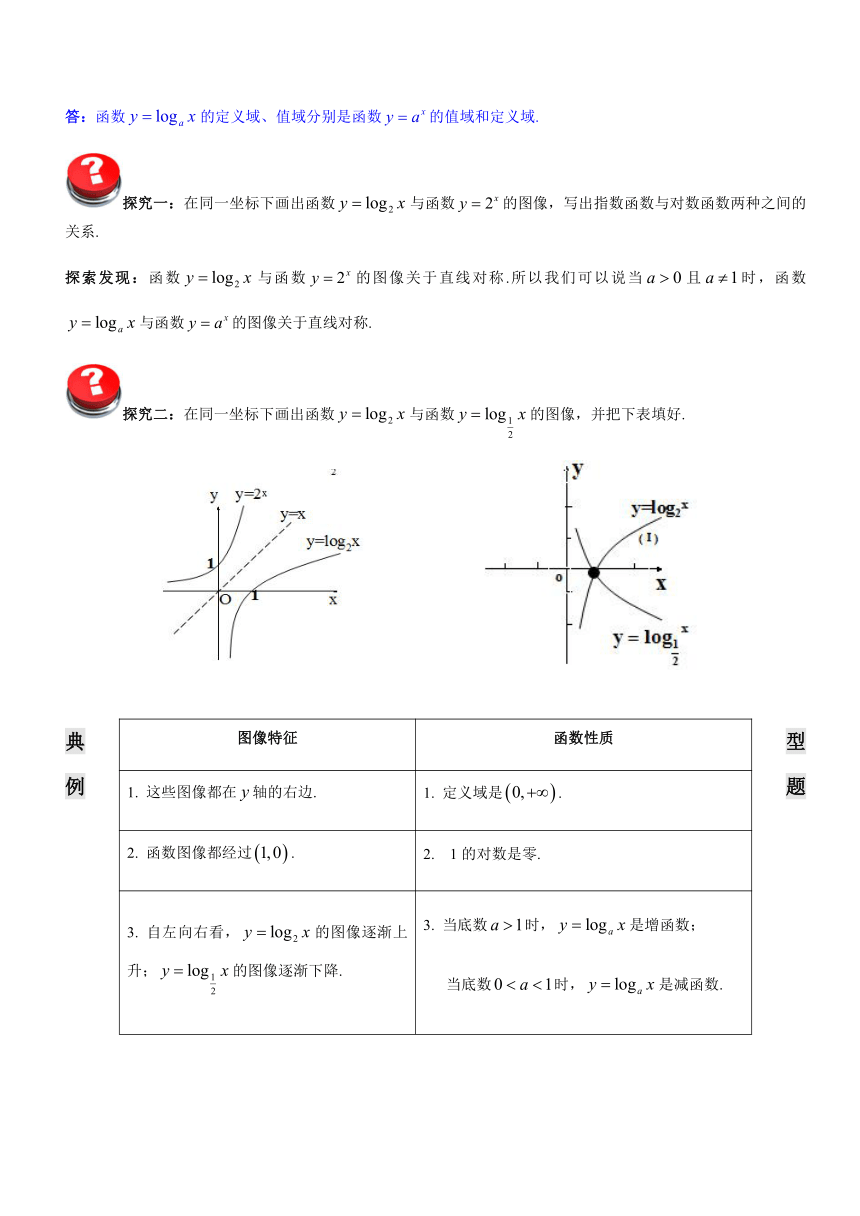
探究一:在同一坐标下画出函数与函数的图像,写出指数函数与对数函数两种之间的关系.
探索发现:函数与函数的图像关于直线对称.所以我们可以说当且时,函数与函数的图像关于直线对称.
探究二:在同一坐标下画出函数与函数的图像,并把下表填好.
图像特征 函数性质
1. 这些图像都在轴的右边. 1. 定义域是.
2. 函数图像都经过. 2. 1的对数是零.
3. 自左向右看,的图像逐渐上升;的图像逐渐下降. 3. 当底数时,是增函数;当底数时,是减函数.
典型例题 .27min.
例1. (★★)求下列函数的定义域:
(1) (2) (3)
解:(1)因为即, 所以函数的定义域为.
(2)因为,即,所以函数的定义域是.
(3)因为,即,所以函数的定义域是.
例2. (★★)比较大小:
(1)和; (2)和; (3)和,其中.
解:(1)因为对数函数在上是增函数,又,所以.
(2)因为对数函数在上是减函数,又,所以.
(3)(i)当时,因为对数函数在上是增函数,
又,所以.
(ii)当时,因为对数函数在上是减函数,
又,所以.
【小结】两个同底数的对数比较大小的一般步骤:
1 确定所要考查的对数函数;
2 根据对数底数判断对数函数增减性;
3 比较真数大小,然后利用对数函数的增减性判断两对数值的大小;
4 若底数与1的大小关系未明确指定时,要分情况对底数进行讨论来比较大小.
例3. (★★)“学习曲线”可以用来描述学习某一任务的速度,假设函数中,表示达到某一英文打字水平(字/分)所需的学习时间(时),表示每分钟打出的字数(字/分). 计算要达到20字/分、40字/分水平所需要的学习时间;(精确到“时”).
解:用计算器计算,得时,;时,.
所以,要达到这两个水平分别需学习时间16小时和37小时.
课堂练习
1. (★★)求下列函数的定义域:
(1),其中; (2),.
解:(1)因为, 所以函数的定义域为.
(2)因为,即,所以函数的定义域是.
2. (★★)比较大小:
(1)和; (2)和;
(3)和,其中.
解:(1)因为对数函数在上是增函数,又,所以.
(2)因为对数函数在上是减函数,又,所以.
(3)(i)当时,因为对数函数在上是增函数,
又,所以.
(ii)当时,因为对数函数在上是减函数,
又,所以.
思考题
(★★★)若真数相同而底数不同时,又如何比较两个对数值的大小呢? 试判断的大小.
解:
【小结】两个底数不相同时底的对数比较大小的一般步骤:
若底数不相同,可在两个对数中插入一个已知 数(如1或0等),间接比较大小.
回顾总结 .3min.
