第1节 比例的意义和基本性质(共20张PPT)
文档属性
| 名称 | 第1节 比例的意义和基本性质(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
在具体的情境中经历比例的形成过程,理解比例的意义,掌握组成比例的关键条件,并能正确地判断两个比能否组成比例。
培养学生进行初步的观察、分析、概括的能力,培养学生学习数学的兴趣。
理解比例的基本性质,认识比例的各部分名称。并能用比例的基本性质正确判断两个比能否组成比例。
同学们都在哪些地方见过国旗呢?
上图中操场上和教室里的两面国旗长和宽的比值有什么关系?
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
操场上的国旗:
教室里的国旗:
长 宽
长 宽
通过计算你发现了什么?
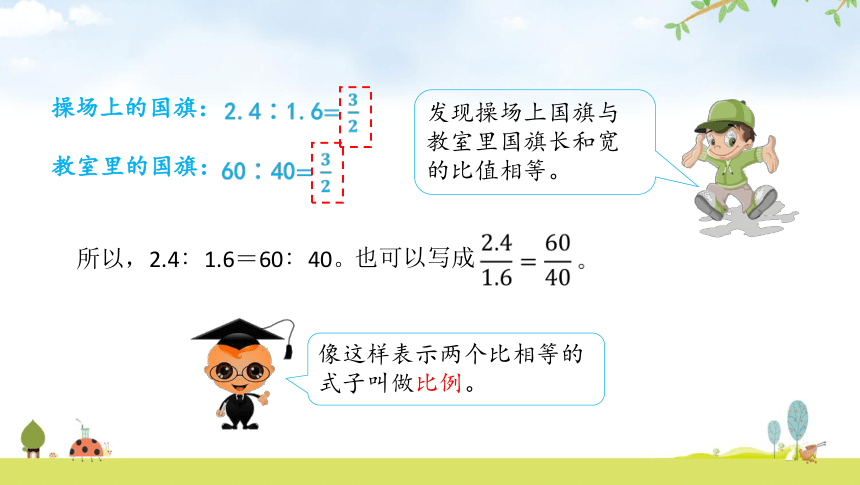
操场上的国旗:
教室里的国旗:
发现操场上国旗与教室里国旗长和宽的比值相等。
像这样表示两个比相等的式子叫做比例。
所以,2.4∶1.6=60∶40。
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
在上图的三面国旗的尺寸中,还有哪些比可以组成比例?
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
2.4:1.6=60:40
如:
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
2.4:1.6=60:40
2.4和40仍然是外项,
1.6和60仍然是内项。
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(1)2.4∶1.6=60∶40
2.4×40=96
1.6×60=96
3×15=____
5×9=____
45
45
两个外项的乘积=两个内项的乘积
两个外项的乘积=两个内项的乘积
再举例子验证你的发现。
例如:2.5∶4和5∶8
2.5×8=20
4×5=20
两个外项的乘积=两个内项的乘积
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
用字母表示比例的基本性质:
=
或
ad= bc
a:b=c:d(b、d≠0)
比例的相关概念
组成比例的四个数叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
表示两个比相等的式子叫做比例。
比例的基本性质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
下面哪组中的两个比可以组成比例?把能组成的比例写出来。
(1)6∶10和9∶15
(2)20∶5和1∶4
6∶10=0.6
9∶15=0.6
所以, 6∶10=9∶15可以组成比例。
20∶5=4
1∶4=0.25
所以, 20∶5和1∶4不能组成比例。
规范解答:
2. 下列各比中哪些能组成比例,请写出来。
0.6∶0.8
3∶1.2
0.5∶0.2
0.6∶0.8=
3∶1.2=0.5∶0.2
规范解答:
计算比值:
0.6∶0.8=3∶4
3∶1.2=5∶2
0.5∶0.2=5∶2
=10∶9
=10∶3
=3∶4
规范解答:
3. 用图中的4个数据可以组成多少个比例?
3∶1.5=4 ∶ 2
3∶4=1.5∶2
2∶1.5=4 ∶ 3
2∶ 4=1.5∶3
1.5∶3=2∶ 4
1.5∶2=3∶4
4∶3=2∶1.5
4∶2=3∶1.5
4. 应用比例的基本性质,判断下面哪组中的两个比可以
组成比例。
(1)6∶3和8∶5
6×5=30
3×8=24
不能组成比例
(2)0.2∶2.5和4∶50
0.2×50=10
2.5×4=10
可以组成比例
规范解答:
0.2∶2.5=4∶50
5. 判断2、4、8、16这四个数能否组成比例?
规范解答:
根据比例的意义判断。
根据比例的基本性质判断。
所以2、4、8、16这四个数能组成比例。
因为
因为
所以
所以
判断:8∶2=4是比例。 ( )
√
×
判断: 8∶2=4是比例。 ( )
错因分析:在比例中,等号的两侧必须都是比。
8∶2=4∶1是比例。
1.从课后习题中选取;
2.完成练习册本课时的习题。
在具体的情境中经历比例的形成过程,理解比例的意义,掌握组成比例的关键条件,并能正确地判断两个比能否组成比例。
培养学生进行初步的观察、分析、概括的能力,培养学生学习数学的兴趣。
理解比例的基本性质,认识比例的各部分名称。并能用比例的基本性质正确判断两个比能否组成比例。
同学们都在哪些地方见过国旗呢?
上图中操场上和教室里的两面国旗长和宽的比值有什么关系?
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
操场上的国旗:
教室里的国旗:
长 宽
长 宽
通过计算你发现了什么?
操场上的国旗:
教室里的国旗:
发现操场上国旗与教室里国旗长和宽的比值相等。
像这样表示两个比相等的式子叫做比例。
所以,2.4∶1.6=60∶40。
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
在上图的三面国旗的尺寸中,还有哪些比可以组成比例?
国旗长2.4m,宽1.6m
国旗长60cm,宽40cm
2.4:1.6=60:40
如:
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
2.4:1.6=60:40
2.4和40仍然是外项,
1.6和60仍然是内项。
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(1)2.4∶1.6=60∶40
2.4×40=96
1.6×60=96
3×15=____
5×9=____
45
45
两个外项的乘积=两个内项的乘积
两个外项的乘积=两个内项的乘积
再举例子验证你的发现。
例如:2.5∶4和5∶8
2.5×8=20
4×5=20
两个外项的乘积=两个内项的乘积
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
用字母表示比例的基本性质:
=
或
ad= bc
a:b=c:d(b、d≠0)
比例的相关概念
组成比例的四个数叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
表示两个比相等的式子叫做比例。
比例的基本性质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
下面哪组中的两个比可以组成比例?把能组成的比例写出来。
(1)6∶10和9∶15
(2)20∶5和1∶4
6∶10=0.6
9∶15=0.6
所以, 6∶10=9∶15可以组成比例。
20∶5=4
1∶4=0.25
所以, 20∶5和1∶4不能组成比例。
规范解答:
2. 下列各比中哪些能组成比例,请写出来。
0.6∶0.8
3∶1.2
0.5∶0.2
0.6∶0.8=
3∶1.2=0.5∶0.2
规范解答:
计算比值:
0.6∶0.8=3∶4
3∶1.2=5∶2
0.5∶0.2=5∶2
=10∶9
=10∶3
=3∶4
规范解答:
3. 用图中的4个数据可以组成多少个比例?
3∶1.5=4 ∶ 2
3∶4=1.5∶2
2∶1.5=4 ∶ 3
2∶ 4=1.5∶3
1.5∶3=2∶ 4
1.5∶2=3∶4
4∶3=2∶1.5
4∶2=3∶1.5
4. 应用比例的基本性质,判断下面哪组中的两个比可以
组成比例。
(1)6∶3和8∶5
6×5=30
3×8=24
不能组成比例
(2)0.2∶2.5和4∶50
0.2×50=10
2.5×4=10
可以组成比例
规范解答:
0.2∶2.5=4∶50
5. 判断2、4、8、16这四个数能否组成比例?
规范解答:
根据比例的意义判断。
根据比例的基本性质判断。
所以2、4、8、16这四个数能组成比例。
因为
因为
所以
所以
判断:8∶2=4是比例。 ( )
√
×
判断: 8∶2=4是比例。 ( )
错因分析:在比例中,等号的两侧必须都是比。
8∶2=4∶1是比例。
1.从课后习题中选取;
2.完成练习册本课时的习题。
