18.2.3 正方形教学课件
图片预览





文档简介
课件15张PPT。2020年春人教版八年级下数学教学课件18.2.3 正方形 创设情景一?问题: 从这个图形中你能得到什么?
你是怎样想到的??┓90° 当? =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.问题: 情景二1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)2.当CD移动到C?D?位置,且 AD? =AB时,此
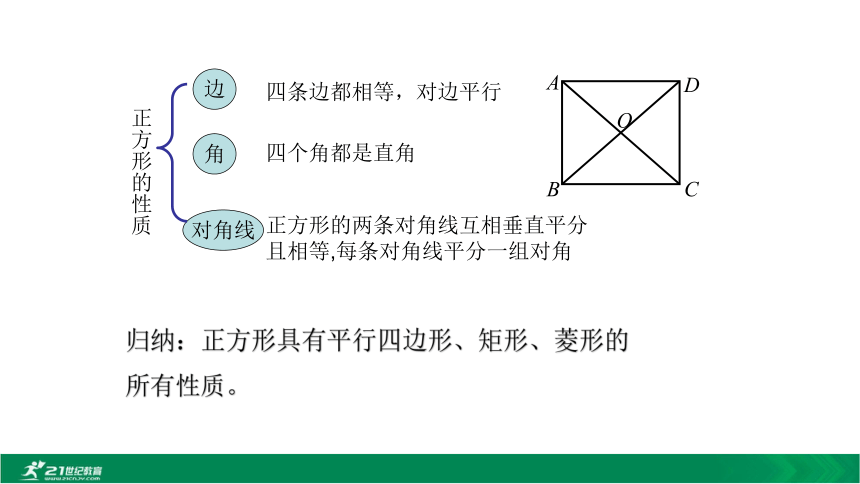
时的图形还是矩形吗?AB 当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.矩 形〃〃正方形邻边相等〃〃一组邻边相等的矩形是正方形一个角是直角正方形∟一个角为直角的菱形是正方形定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.正方形判定正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角四条边都相等,对边平行四个角都是直角边对角线角正方形的性质归纳:正方形具有平行四边形、矩形、菱形的所有性质。平行四边形矩形菱形正
方
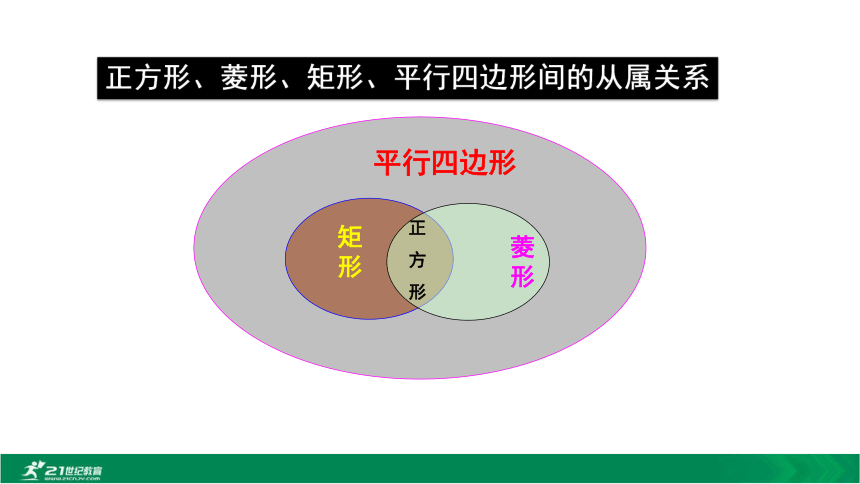
形正方形、菱形、矩形、平行四边形间的从属关系例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °D12cm112.5 °4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.530°5.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.6.正方形具有而矩形不一定具有的性质是( )
A、四个角相等
B、对角线互相垂直
C、对角互补
D、对角线相等7.正方形具有而菱形不一定具有的性质( )
A、四条边相等
B、对角线互相垂直平分
C、对角线平分一组对角
D、对角线相等 BD8.根据图形所具有的性质,在下表中相应的空格里打“ √ ” √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
你是怎样想到的??┓90° 当? =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.问题: 情景二1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)2.当CD移动到C?D?位置,且 AD? =AB时,此
时的图形还是矩形吗?AB 当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.矩 形〃〃正方形邻边相等〃〃一组邻边相等的矩形是正方形一个角是直角正方形∟一个角为直角的菱形是正方形定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.正方形判定正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角四条边都相等,对边平行四个角都是直角边对角线角正方形的性质归纳:正方形具有平行四边形、矩形、菱形的所有性质。平行四边形矩形菱形正
方
形正方形、菱形、矩形、平行四边形间的从属关系例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °D12cm112.5 °4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.530°5.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.6.正方形具有而矩形不一定具有的性质是( )
A、四个角相等
B、对角线互相垂直
C、对角互补
D、对角线相等7.正方形具有而菱形不一定具有的性质( )
A、四条边相等
B、对角线互相垂直平分
C、对角线平分一组对角
D、对角线相等 BD8.根据图形所具有的性质,在下表中相应的空格里打“ √ ” √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
