人教版高中物理必修2第五章 5.1 曲线运动课件(共32张PPT)
文档属性
| 名称 | 人教版高中物理必修2第五章 5.1 曲线运动课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-26 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
第五章 曲线运动
第 1 节:曲线运动
人教版高中物理必修二
1. 知道曲线运动是一种变速运动。
2. 初步认识运动的合成与分解。
3. 知道曲线运动的位移和瞬时速度的方向,能在曲线运动的轨迹图上画出各点的速度方向。
4. 知道物体做曲线运动的条件,能运用牛顿第二定律分析做曲线运动的条件。
首先利用视频《生活中的曲线运动》及嫦娥一号轨迹模拟图,向学生展示一些常见的曲线运动形式,导入新课并总结出曲线运动的概念;接着根据位移为矢量的特点,利用平面直角坐标系与数学中的切线概念,分析做曲线运动物体的位移与速度 ,得出曲线运动是变速运动的结论;之后通过分析蜡块的运动实例,让学生体会分析物体在平面中运动的一种方法;最后利用三个对比试验得出物体做曲线运动的条件。
本节课的重点是曲线运动速度方向的理解及曲线运动的分析方法,课件首先通过分析链球运动与小球在分段管道内的运动,得出曲线运动的速度是时刻变化的,再利用切线的概念结合动画的直观性得出曲线运动的速度方向;在研究蜡块运动时,从轨迹、位移、速度等刚面入手,逐步分析出蜡块运动的特点,让学生体会利用速度的合成与分解来分析曲线运动过程。
生活中的曲线运动
地球
月球
嫦娥一号轨迹模拟图
曲线运动
物体运动轨迹为曲线的运动叫曲线运动。
曲线运动是普遍的运动情形。
大到宏观世界(如天体运行),小到微观世界(如电子绕原子核旋转),生活中如烟花、投标枪、铁饼、跳高、跳远等均为曲线运动。
怎样描述曲线运动呢?
O
x
y
A
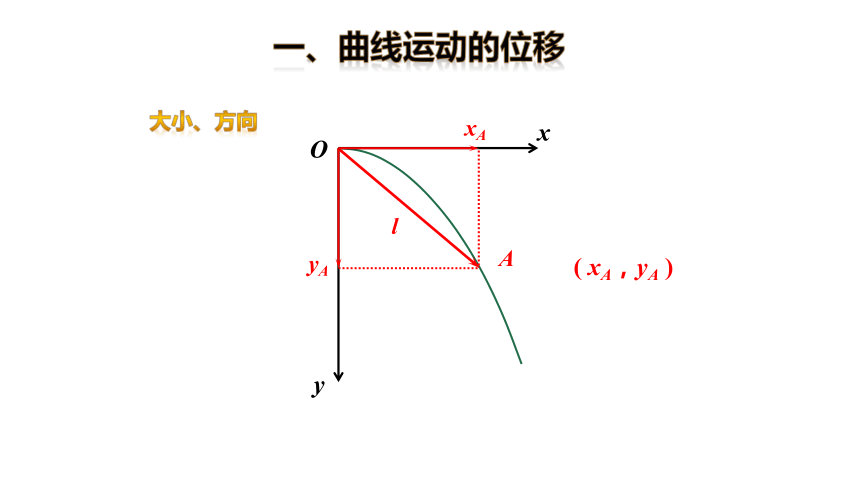
xA
yA
( xA,yA )
l
一、曲线运动的位移
大小、方向
放手的位置不同,链球飞出去的方向相同吗?
这说明了什么?
速度方向时刻在改变!
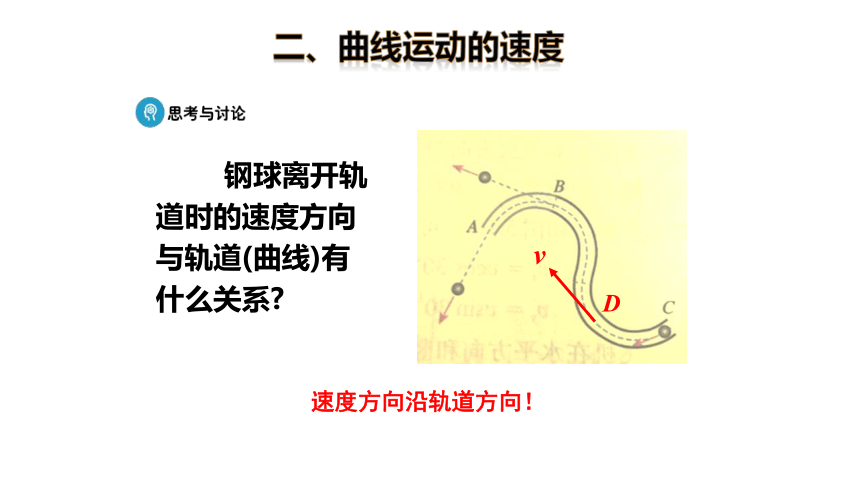
二、曲线运动的速度
D
v
二、曲线运动的速度
钢球离开轨道时的速度方向与轨道(曲线)有什么关系?
速度方向沿轨道方向!
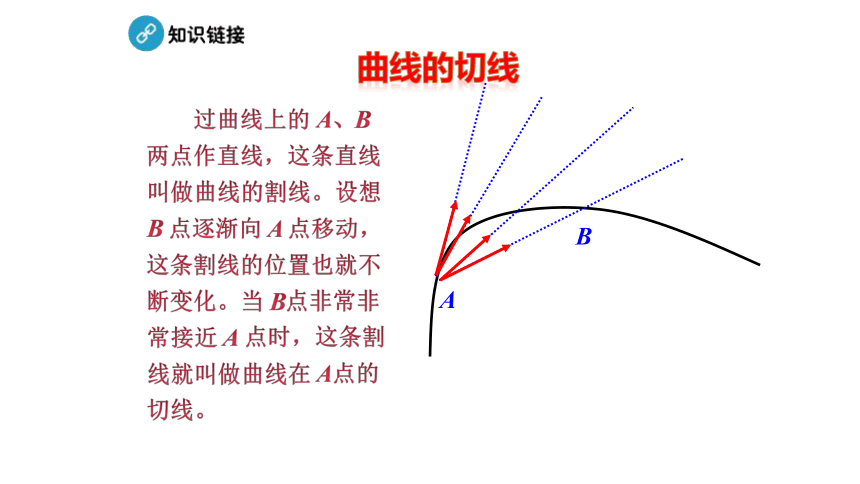
A
B
过曲线上的 A、B 两点作直线,这条直线叫做曲线的割线。设想 B 点逐渐向 A 点移动,这条割线的位置也就不断变化。当 B点非常非常接近 A 点时,这条割线就叫做曲线在 A点的切线。
曲线的切线
质点在某一点(或某一时刻)的速度方向,沿曲线在这一点的切线方向。
结 论
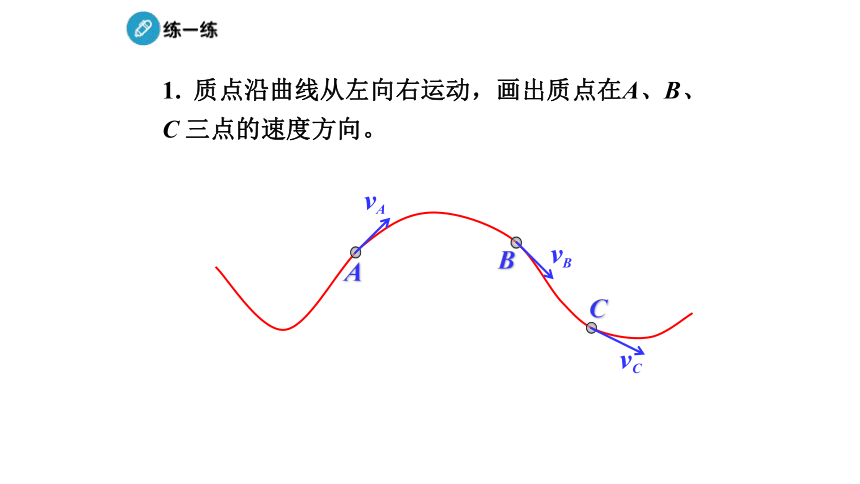
1. 质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
A
B
C
vA
vB
vC
O
x
y
A
xA
yA
l
v
θ
vx
vy
vy= vsin θ
vx= vcos θ
曲线运动是变速运动
2. 飞机起飞时以 300 km/h 的速度斜向上飞,飞行方向与水平方向的夹角为 30 度。求水平方向的分速度和竖直方向的分速度。
v
vx
vy
30°
vy= vsin 30°= 150 km/h
vx= vcos 30°= 260 km/h
1. 曲线运动是变速运动,但变速运动不一定是曲线运动。
2. 曲线运动的速度大小不一定变化,但方向一定变化。
3. 曲线运动的速度方向时刻发生变化,故加速度不为 0,即做曲线运动的物体的合力一定不为零。
曲线运动的性质
三、运动的描述实例
蜡块在做什么样的运动?
红蜡块的运动
蜡块任一时刻的位置
设蜡块竖直向上的速度为 vy
蜡块水平向右的速度为 vx
任一时刻的 x 坐标 x = vx t
任一时刻的 y 坐标 y = vy t
蜡块在 P 点的位置可以用它的坐标 ( x,y ) 表示
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
蜡块的实际运动轨迹是一条倾斜的直线
蜡块的运动轨迹
x = vx t
y = vy t
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
由于 vx 和 vy 都是定值
是过原点的直线
在 t 时刻蜡块运动的位移大小
蜡块运动的位移的方向
蜡块的运动位移
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
求出 θ 就可得知蜡块运动的位移的方向
θ
蜡块做的是速度为 v 的匀速直线运动
蜡块的运动速度
蜡块运动的速度
O
x
y
P
x = vx t
y = vy t
v
是定值
θ
O
x
y
蜡块的实际运动 v
沿着 OP 做匀速直线运动
分运动
合运动
分运动
v
蜡块的运动
vx
vy
P
蜡块的实际运动 v 是由水平运动 vx 和竖直运动 vy 合成的
1. 合运动:物体实际发生的运动
2. 分运动:物体同时参与几个运动
3. 运动的合成:已知分运动求合运动
4. 运动的分解:已知合运动求分运动
运动的合成与分解
5. 合运动与分运动的关系及特点
(1) 等时性:分运动和合运动同时开始,同时进行,同时结束。
(2) 独立性:物体可同时参与几个不同的分运动,各分运动独立进行,互不影响
(3) 等效性:合运动与分运动在效果上是等效替代的关系。
(4) 同一性:合运动与分运动必须对同一物体。
位移的合成
速度的合成
加速度的合成
速度、位移、加速度都是矢量,合成时均遵循平行四边形定则。
6. a、v、x 的合成与分解
分位移 x1
合位移 x
分位移x2
分速度 v1
合速度 v
分速度 v2
分运动的加速度 a1
合运动的加速度 a
分运动的加速度a2
7. 运动分解的原则
(1) 等效性原则:两个分运动的效果与合运动的实际效果,完全等效,可以互相替代。
(2) 符合实际的原则:根据分运动的实际效果将合运动分解。
(3) 解题方便的原则:根据解题的需要按具体情况进行分解。
四、物体做曲线运动的条件
三个对比实验
1. 在光滑的水平面上具有某一初速度的小球在不受外力时
将如何运动?
2. 在光滑的水平面上具有某一初速度的小球在运动方向的
正前方向或正后方向放一条形磁铁将如何运动?
由于小球在运动方向受磁铁作用,会使小球加速或减速,
但仍做直线运动
匀速直线运动
v
3. 在光滑的水平面上具有某一初速度的小球在运动方
向一侧放一条形磁铁时小球将如何运动?
由于小球在运动过程中受到一个侧力,小球将改变轨迹而做曲线运动
当物体所受的合力方向跟它的速度方向不在同一直线上时,物体做曲线运动。
v
质点在某一点(或某一时刻)的速度方向,沿曲线在这一点的切线方向。
1. 曲线运动的位移
2. 曲线运动的速度
3. 运动描述的实例
4. 物体做曲线运动的条件
当物体所受的合力方向跟它的速度方向不在同一直线上时,物体做曲线运动。
1. 某物体做曲线运动,在一段时间内其位移大小为 50 m,则这段时间内物体通过的路程一定 50 m。
大于
2. 小球在水平桌面上做匀速直线运动,当它受到如图
所示方向的力的作用时,小球可能运动的方向是 ( )
A. Oa B. Ob C. Oc D. Od
D
3.如图所示,曲线为质点运动的轨迹,在通过位置 P 时速度、加速度及 P 附近的一段轨迹都在图上标出,其中可能正确的是 ( )
BD
C
4. 如图所示,物体在恒力的作用下沿从 A 曲线运动到 B,
此时突然使力反向,物体的运动情况是 ( )
A. 物体可能沿曲线 Ba 运动
B. 物体可能沿直线 Bb 运动
C. 物体可能沿曲线 Bc 运动
D. 物体可能沿曲线 B 返回 A
null
null
谢谢欣赏!
第五章 曲线运动
第 1 节:曲线运动
人教版高中物理必修二
1. 知道曲线运动是一种变速运动。
2. 初步认识运动的合成与分解。
3. 知道曲线运动的位移和瞬时速度的方向,能在曲线运动的轨迹图上画出各点的速度方向。
4. 知道物体做曲线运动的条件,能运用牛顿第二定律分析做曲线运动的条件。
首先利用视频《生活中的曲线运动》及嫦娥一号轨迹模拟图,向学生展示一些常见的曲线运动形式,导入新课并总结出曲线运动的概念;接着根据位移为矢量的特点,利用平面直角坐标系与数学中的切线概念,分析做曲线运动物体的位移与速度 ,得出曲线运动是变速运动的结论;之后通过分析蜡块的运动实例,让学生体会分析物体在平面中运动的一种方法;最后利用三个对比试验得出物体做曲线运动的条件。
本节课的重点是曲线运动速度方向的理解及曲线运动的分析方法,课件首先通过分析链球运动与小球在分段管道内的运动,得出曲线运动的速度是时刻变化的,再利用切线的概念结合动画的直观性得出曲线运动的速度方向;在研究蜡块运动时,从轨迹、位移、速度等刚面入手,逐步分析出蜡块运动的特点,让学生体会利用速度的合成与分解来分析曲线运动过程。
生活中的曲线运动
地球
月球
嫦娥一号轨迹模拟图
曲线运动
物体运动轨迹为曲线的运动叫曲线运动。
曲线运动是普遍的运动情形。
大到宏观世界(如天体运行),小到微观世界(如电子绕原子核旋转),生活中如烟花、投标枪、铁饼、跳高、跳远等均为曲线运动。
怎样描述曲线运动呢?
O
x
y
A
xA
yA
( xA,yA )
l
一、曲线运动的位移
大小、方向
放手的位置不同,链球飞出去的方向相同吗?
这说明了什么?
速度方向时刻在改变!
二、曲线运动的速度
D
v
二、曲线运动的速度
钢球离开轨道时的速度方向与轨道(曲线)有什么关系?
速度方向沿轨道方向!
A
B
过曲线上的 A、B 两点作直线,这条直线叫做曲线的割线。设想 B 点逐渐向 A 点移动,这条割线的位置也就不断变化。当 B点非常非常接近 A 点时,这条割线就叫做曲线在 A点的切线。
曲线的切线
质点在某一点(或某一时刻)的速度方向,沿曲线在这一点的切线方向。
结 论
1. 质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
A
B
C
vA
vB
vC
O
x
y
A
xA
yA
l
v
θ
vx
vy
vy= vsin θ
vx= vcos θ
曲线运动是变速运动
2. 飞机起飞时以 300 km/h 的速度斜向上飞,飞行方向与水平方向的夹角为 30 度。求水平方向的分速度和竖直方向的分速度。
v
vx
vy
30°
vy= vsin 30°= 150 km/h
vx= vcos 30°= 260 km/h
1. 曲线运动是变速运动,但变速运动不一定是曲线运动。
2. 曲线运动的速度大小不一定变化,但方向一定变化。
3. 曲线运动的速度方向时刻发生变化,故加速度不为 0,即做曲线运动的物体的合力一定不为零。
曲线运动的性质
三、运动的描述实例
蜡块在做什么样的运动?
红蜡块的运动
蜡块任一时刻的位置
设蜡块竖直向上的速度为 vy
蜡块水平向右的速度为 vx
任一时刻的 x 坐标 x = vx t
任一时刻的 y 坐标 y = vy t
蜡块在 P 点的位置可以用它的坐标 ( x,y ) 表示
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
蜡块的实际运动轨迹是一条倾斜的直线
蜡块的运动轨迹
x = vx t
y = vy t
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
由于 vx 和 vy 都是定值
是过原点的直线
在 t 时刻蜡块运动的位移大小
蜡块运动的位移的方向
蜡块的运动位移
O
x
y
P
(vx t,vy t )
x = vx t
y = vy t
求出 θ 就可得知蜡块运动的位移的方向
θ
蜡块做的是速度为 v 的匀速直线运动
蜡块的运动速度
蜡块运动的速度
O
x
y
P
x = vx t
y = vy t
v
是定值
θ
O
x
y
蜡块的实际运动 v
沿着 OP 做匀速直线运动
分运动
合运动
分运动
v
蜡块的运动
vx
vy
P
蜡块的实际运动 v 是由水平运动 vx 和竖直运动 vy 合成的
1. 合运动:物体实际发生的运动
2. 分运动:物体同时参与几个运动
3. 运动的合成:已知分运动求合运动
4. 运动的分解:已知合运动求分运动
运动的合成与分解
5. 合运动与分运动的关系及特点
(1) 等时性:分运动和合运动同时开始,同时进行,同时结束。
(2) 独立性:物体可同时参与几个不同的分运动,各分运动独立进行,互不影响
(3) 等效性:合运动与分运动在效果上是等效替代的关系。
(4) 同一性:合运动与分运动必须对同一物体。
位移的合成
速度的合成
加速度的合成
速度、位移、加速度都是矢量,合成时均遵循平行四边形定则。
6. a、v、x 的合成与分解
分位移 x1
合位移 x
分位移x2
分速度 v1
合速度 v
分速度 v2
分运动的加速度 a1
合运动的加速度 a
分运动的加速度a2
7. 运动分解的原则
(1) 等效性原则:两个分运动的效果与合运动的实际效果,完全等效,可以互相替代。
(2) 符合实际的原则:根据分运动的实际效果将合运动分解。
(3) 解题方便的原则:根据解题的需要按具体情况进行分解。
四、物体做曲线运动的条件
三个对比实验
1. 在光滑的水平面上具有某一初速度的小球在不受外力时
将如何运动?
2. 在光滑的水平面上具有某一初速度的小球在运动方向的
正前方向或正后方向放一条形磁铁将如何运动?
由于小球在运动方向受磁铁作用,会使小球加速或减速,
但仍做直线运动
匀速直线运动
v
3. 在光滑的水平面上具有某一初速度的小球在运动方
向一侧放一条形磁铁时小球将如何运动?
由于小球在运动过程中受到一个侧力,小球将改变轨迹而做曲线运动
当物体所受的合力方向跟它的速度方向不在同一直线上时,物体做曲线运动。
v
质点在某一点(或某一时刻)的速度方向,沿曲线在这一点的切线方向。
1. 曲线运动的位移
2. 曲线运动的速度
3. 运动描述的实例
4. 物体做曲线运动的条件
当物体所受的合力方向跟它的速度方向不在同一直线上时,物体做曲线运动。
1. 某物体做曲线运动,在一段时间内其位移大小为 50 m,则这段时间内物体通过的路程一定 50 m。
大于
2. 小球在水平桌面上做匀速直线运动,当它受到如图
所示方向的力的作用时,小球可能运动的方向是 ( )
A. Oa B. Ob C. Oc D. Od
D
3.如图所示,曲线为质点运动的轨迹,在通过位置 P 时速度、加速度及 P 附近的一段轨迹都在图上标出,其中可能正确的是 ( )
BD
C
4. 如图所示,物体在恒力的作用下沿从 A 曲线运动到 B,
此时突然使力反向,物体的运动情况是 ( )
A. 物体可能沿曲线 Ba 运动
B. 物体可能沿直线 Bb 运动
C. 物体可能沿曲线 Bc 运动
D. 物体可能沿曲线 B 返回 A
null
null
谢谢欣赏!
