北师大版八年级数学下册 1.1 等腰三角形课件(第2课时 共32张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 1.1 等腰三角形课件(第2课时 共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 12:06:37 | ||
图片预览






文档简介
(共33张PPT)
1.1 等腰三角形
第2课时 等边三角形的性质
第1章 三角形的证明
北师版八年级数学下册
等腰三角形有哪些性质?
1.等腰三角形的性质:等边对等角.
2.等腰三角形性质的推论:三线合一,即等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
复习导入
一. 等腰三角形中相等的线段
在等腰三角形中画出一些线段(如角平分线、中线、高等),你能发现其 中一些相等的线段吗?能证明你的结论吗?
新知探究
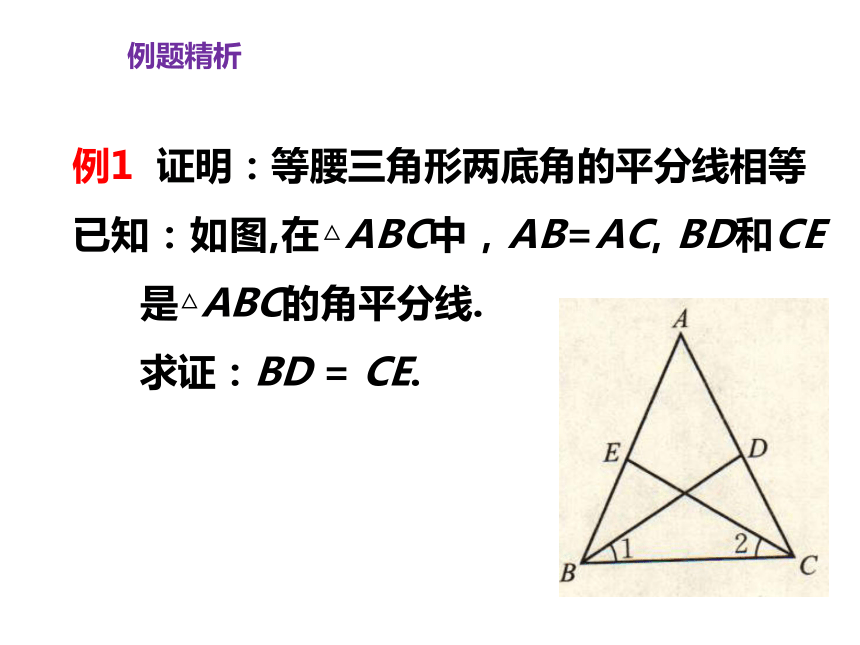
例1 证明:等腰三角形两底角的平分线相等
已知:如图,在△ABC中,AB=AC, BD和CE是△ABC的角平分线.
求证:BD = CE.
例题精析
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD,CE分别平分∠ABC 和∠ACB ,
∴ ∠1=∠2.
在△BDC和△CEB中,
∠ ACB=∠ ABC, BC=CB, ∠1=∠2,
∴△BDC≌△CEB (ASA).
∴BD=CE(全等三角形的对应边相等).
证明:
例题精析
例2 求证:等腰三角形两腰上的中线相等.
思路点拨:
先根据命题分析出题设和结论,画出图形,写出已知和求证,然后利用等腰三角形的性质和三角形全等的知识证明.
例题精析
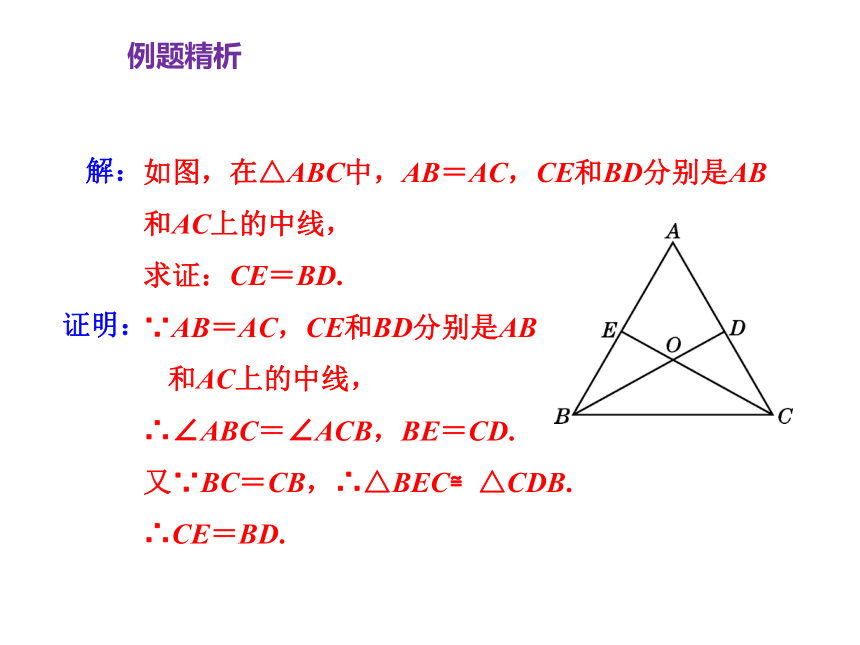
解:
如图,在△ABC中,AB=AC,CE和BD分别是AB
和AC上的中线,
求证:CE=BD.
∵AB=AC,CE和BD分别是AB
和AC上的中线,
∴∠ABC=∠ACB,BE=CD.
又∵BC=CB,∴△BEC≌△CDB.
∴CE=BD.
证明:
例题精析
二. 等边三角形的性质
1.等边三角形的定义是什么?
2.想一想
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
新知探究
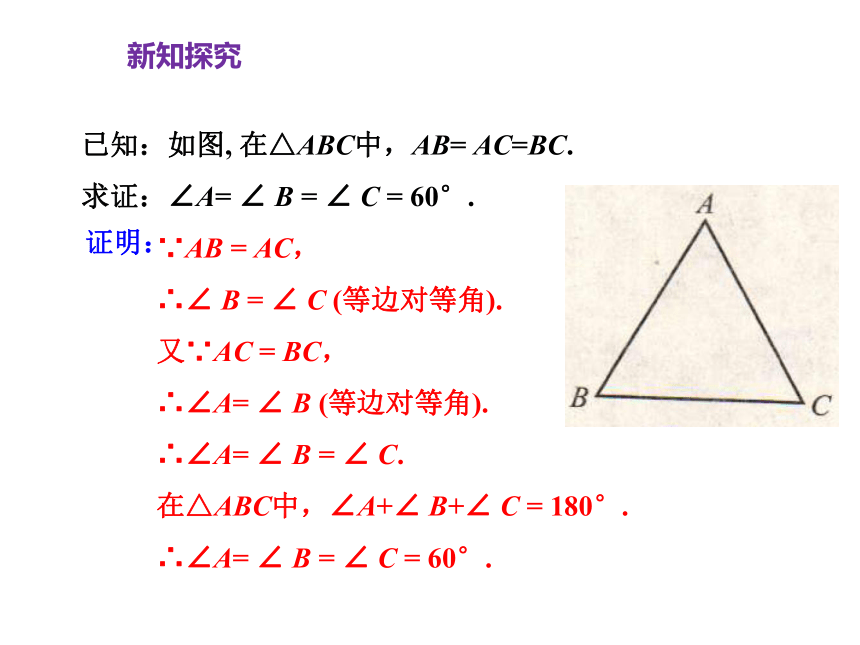
定理 等边三角形的三个内角都相等,并且每个角都等于60°.
已知:如图, 在△ABC中,AB= AC=BC.
求证:∠A= ∠ B = ∠ C = 60°.
∵AB = AC,
∴∠ B = ∠ C (等边对等角).
又∵AC = BC,
∴∠A= ∠ B (等边对等角).
∴∠A= ∠ B = ∠ C.
在△ABC中,∠A+∠ B+∠ C = 180°.
∴∠A= ∠ B = ∠ C = 60°.
证明:
新知探究
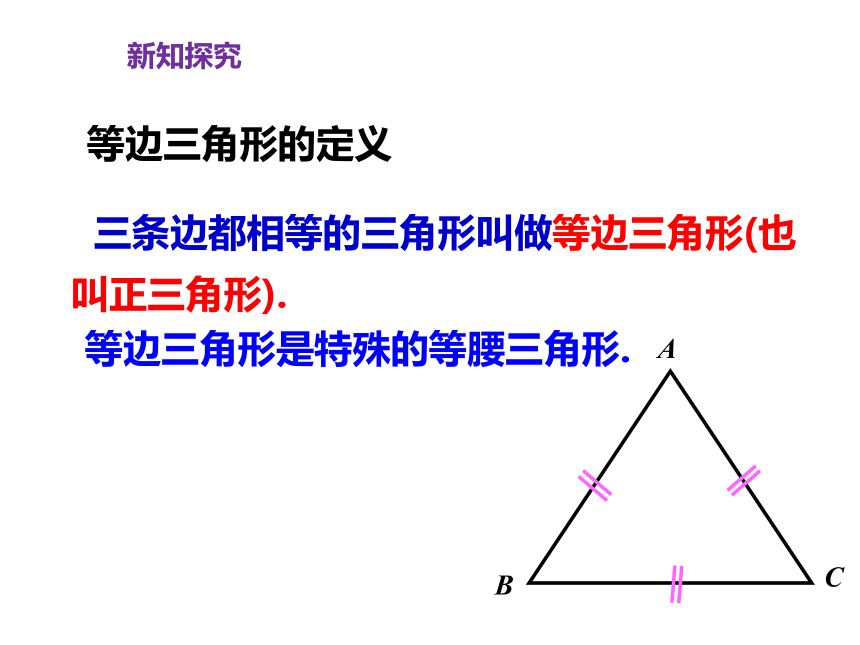
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形).
等边三角形是特殊的等腰三角形.
新知探究
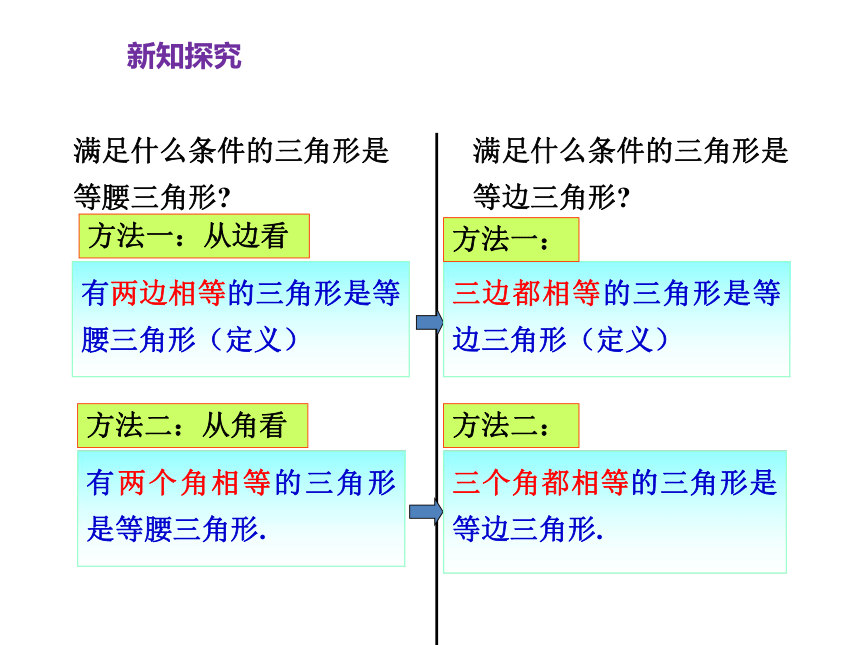
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
方法一:
方法二:
新知探究
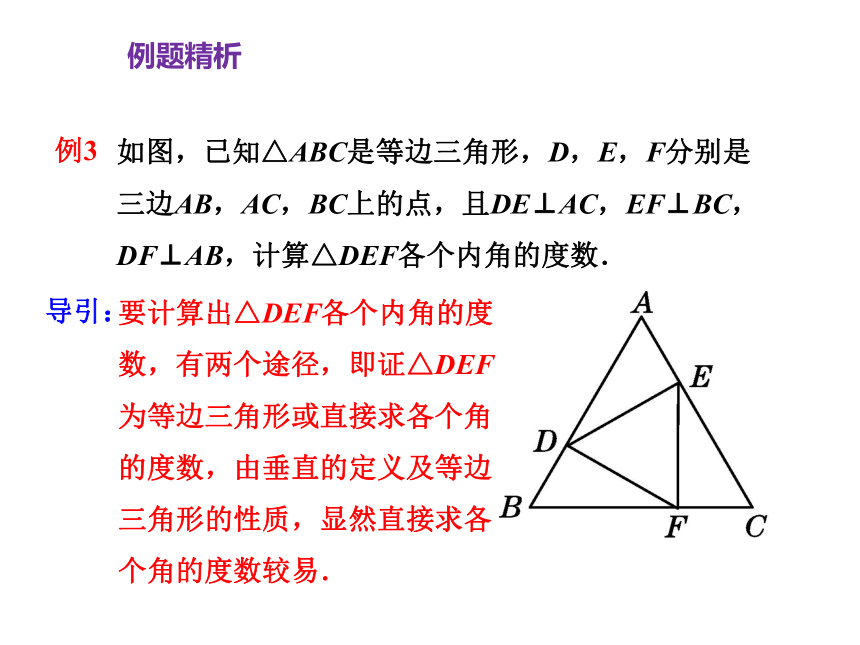
如图,已知△ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点,且DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF各个内角的度数.
例3
导引:
要计算出△DEF各个内角的度
数,有两个途径,即证△DEF
为等边三角形或直接求各个角
的度数,由垂直的定义及等边
三角形的性质,显然直接求各
个角的度数较易.
例题精析
因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°.
因为DE⊥AC,EF⊥BC,DF⊥AB,
所以∠AED=∠EFC=∠FDB=90°.
所以∠ADE=90°-∠A=90°-60°=30°.
所以∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
解:
例题精析
方法总结
利用等边三角形的性质求角的度数时,通过利
用等边三角形的三个内角都相等,并且每一个角都等于60°的性质,找出要求角与已知角间的关系来进行相关计算;有时还要结合全等图形等知识来解决.
例题精析
如图,已知△ABC,△BDE都是等边三角形.
求证:AE=CD.
例4
导引:
要证AE=CD,可通过证AE,
CD所在的两个三角形全等来
实现,即证△ABE≌△CBD,
条件可从等边三角形中去寻
找.
例题精析
∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).
∴AE=CD.
证明:
例题精析
方法总结
运用等边三角形性质证明线段相等的方法:
把要证的两条线段放到一个三角形中证其为等腰或
等边三角形或者放到两个三角形中,利用全等三角
形的性质证明;注意等边三角形的三个内角相等、
三条边相等、三线合一是隐含的已知条件.
例题精析
1. 在等腰三角形ABC中,AB=AC,那么下列说法中不正确的是( )
A.BC边上的高线和中线互相重合
B.AB和AC边上的中线相等
C.顶点B处的角平分线和顶点C处的角平分线相等D.AB,BC边上的高线相等
课堂精练
D
2. 如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE为AC,AB边上的高
B.BD,CE都为△ABC的角平分线
C.∠ABD= ∠ABC,
∠ACE= ∠ACB
D.∠ABD=∠BCE
D
课堂精练
3. 求等边三角形两条中线相交所成锐角的度数.
解:
如图,在等边三角形ABC中,CE,BF分别是AB,AC边上的中线,且CE与BF相交于点O,
则CE垂直平分AB,BF垂直平分AC,
在Rt△ABF中,∵∠A=60°,
∴∠ABF=30°.
在Rt△BEO中,∵∠EBO=30°,∴∠EOB=60°,
即等边三角形两条中线相交所成锐角的度数为60°.
课堂精练
4. 如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.
解:
由题意易知,
BD=DE=AD,
∴∠DBA=∠BAD.
又∵∠DBA+∠BAD=∠ADE=60°,
∴∠BAD=30°.同理可得,∠CAE=30°,
∴∠BAC=∠BAD+∠DAE+∠CAE
=30°+60°+30°=120°.
课堂精练
5. 下面关于等边三角形的说法正确的有( )
①三个角都相等;②三条边都相等;③是一种特殊的等腰三角形;④是一种特殊的直角三角形.
A.1个 B.2个
C.3个 D.4个
C
课堂精练
6. 已知AD是等边三角形ABC的高,且BD=1 cm,那么BC的长是( )
A.1 cm B.2 cm
C.3 cm D.4 cm
B
课堂精练
7. 如图,在等边三角形ABC中,BD,CE是两条中线,则∠1的度数为( )
A.90°
B.30°
C.120°
D.150°
C
课堂精练
8.【中考·南充】如图,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1,1)
B.( ,1)
C.( , )
D.(1, )
D
课堂精练
9. 如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3
B.2
C.1
D.0
A
课堂精练
10. 如图,l∥m,等边三角形ABC的顶点B在直线m上,边BC与直线m所夹角为20°,则∠α的度数为( )
A.60°
B.45°
C.40°
D.30°
C
课堂精练
11. 如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45°
B.55°
C.60°
D.75°
C
课堂精练
已知△ABC是等边三角形,设AB,BC,AC边上的中线交于点G,∠BAC,∠ABC,∠ACB的平分线交于点I,AB,BC,AC边上的高交于点H,则下列结论:①点G与点I一定重合;②点G与点H一定重合;③点I与点H一定重合;④点G,点I与点H一定重合.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
易错点拨
因为等边三角形的三条边相等,所以等边三角形每条边上的中线、高与该边对角的平分线互相重合,所以点G,点I与点H一定重合.
易错点拨
1.等腰三角形的特殊性质:
(1)等腰三角形两底角的平分线相等;
(2)等腰三角形两腰上的高相等;
(3)等腰三角形两腰上的中线相等;
课堂小结
2.等边三角形的性质:
(1) 等边三角形的三边都相等;
(2) 等边三角形的三个内角都相等,并且每个角都等
于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分
别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长
度相等.
课堂小结
1.1 等腰三角形
第2课时 等边三角形的性质
第1章 三角形的证明
北师版八年级数学下册
等腰三角形有哪些性质?
1.等腰三角形的性质:等边对等角.
2.等腰三角形性质的推论:三线合一,即等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
复习导入
一. 等腰三角形中相等的线段
在等腰三角形中画出一些线段(如角平分线、中线、高等),你能发现其 中一些相等的线段吗?能证明你的结论吗?
新知探究
例1 证明:等腰三角形两底角的平分线相等
已知:如图,在△ABC中,AB=AC, BD和CE是△ABC的角平分线.
求证:BD = CE.
例题精析
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD,CE分别平分∠ABC 和∠ACB ,
∴ ∠1=∠2.
在△BDC和△CEB中,
∠ ACB=∠ ABC, BC=CB, ∠1=∠2,
∴△BDC≌△CEB (ASA).
∴BD=CE(全等三角形的对应边相等).
证明:
例题精析
例2 求证:等腰三角形两腰上的中线相等.
思路点拨:
先根据命题分析出题设和结论,画出图形,写出已知和求证,然后利用等腰三角形的性质和三角形全等的知识证明.
例题精析
解:
如图,在△ABC中,AB=AC,CE和BD分别是AB
和AC上的中线,
求证:CE=BD.
∵AB=AC,CE和BD分别是AB
和AC上的中线,
∴∠ABC=∠ACB,BE=CD.
又∵BC=CB,∴△BEC≌△CDB.
∴CE=BD.
证明:
例题精析
二. 等边三角形的性质
1.等边三角形的定义是什么?
2.想一想
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
新知探究
定理 等边三角形的三个内角都相等,并且每个角都等于60°.
已知:如图, 在△ABC中,AB= AC=BC.
求证:∠A= ∠ B = ∠ C = 60°.
∵AB = AC,
∴∠ B = ∠ C (等边对等角).
又∵AC = BC,
∴∠A= ∠ B (等边对等角).
∴∠A= ∠ B = ∠ C.
在△ABC中,∠A+∠ B+∠ C = 180°.
∴∠A= ∠ B = ∠ C = 60°.
证明:
新知探究
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形).
等边三角形是特殊的等腰三角形.
新知探究
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
方法一:
方法二:
新知探究
如图,已知△ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点,且DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF各个内角的度数.
例3
导引:
要计算出△DEF各个内角的度
数,有两个途径,即证△DEF
为等边三角形或直接求各个角
的度数,由垂直的定义及等边
三角形的性质,显然直接求各
个角的度数较易.
例题精析
因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°.
因为DE⊥AC,EF⊥BC,DF⊥AB,
所以∠AED=∠EFC=∠FDB=90°.
所以∠ADE=90°-∠A=90°-60°=30°.
所以∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
解:
例题精析
方法总结
利用等边三角形的性质求角的度数时,通过利
用等边三角形的三个内角都相等,并且每一个角都等于60°的性质,找出要求角与已知角间的关系来进行相关计算;有时还要结合全等图形等知识来解决.
例题精析
如图,已知△ABC,△BDE都是等边三角形.
求证:AE=CD.
例4
导引:
要证AE=CD,可通过证AE,
CD所在的两个三角形全等来
实现,即证△ABE≌△CBD,
条件可从等边三角形中去寻
找.
例题精析
∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).
∴AE=CD.
证明:
例题精析
方法总结
运用等边三角形性质证明线段相等的方法:
把要证的两条线段放到一个三角形中证其为等腰或
等边三角形或者放到两个三角形中,利用全等三角
形的性质证明;注意等边三角形的三个内角相等、
三条边相等、三线合一是隐含的已知条件.
例题精析
1. 在等腰三角形ABC中,AB=AC,那么下列说法中不正确的是( )
A.BC边上的高线和中线互相重合
B.AB和AC边上的中线相等
C.顶点B处的角平分线和顶点C处的角平分线相等D.AB,BC边上的高线相等
课堂精练
D
2. 如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE为AC,AB边上的高
B.BD,CE都为△ABC的角平分线
C.∠ABD= ∠ABC,
∠ACE= ∠ACB
D.∠ABD=∠BCE
D
课堂精练
3. 求等边三角形两条中线相交所成锐角的度数.
解:
如图,在等边三角形ABC中,CE,BF分别是AB,AC边上的中线,且CE与BF相交于点O,
则CE垂直平分AB,BF垂直平分AC,
在Rt△ABF中,∵∠A=60°,
∴∠ABF=30°.
在Rt△BEO中,∵∠EBO=30°,∴∠EOB=60°,
即等边三角形两条中线相交所成锐角的度数为60°.
课堂精练
4. 如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.
解:
由题意易知,
BD=DE=AD,
∴∠DBA=∠BAD.
又∵∠DBA+∠BAD=∠ADE=60°,
∴∠BAD=30°.同理可得,∠CAE=30°,
∴∠BAC=∠BAD+∠DAE+∠CAE
=30°+60°+30°=120°.
课堂精练
5. 下面关于等边三角形的说法正确的有( )
①三个角都相等;②三条边都相等;③是一种特殊的等腰三角形;④是一种特殊的直角三角形.
A.1个 B.2个
C.3个 D.4个
C
课堂精练
6. 已知AD是等边三角形ABC的高,且BD=1 cm,那么BC的长是( )
A.1 cm B.2 cm
C.3 cm D.4 cm
B
课堂精练
7. 如图,在等边三角形ABC中,BD,CE是两条中线,则∠1的度数为( )
A.90°
B.30°
C.120°
D.150°
C
课堂精练
8.【中考·南充】如图,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1,1)
B.( ,1)
C.( , )
D.(1, )
D
课堂精练
9. 如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3
B.2
C.1
D.0
A
课堂精练
10. 如图,l∥m,等边三角形ABC的顶点B在直线m上,边BC与直线m所夹角为20°,则∠α的度数为( )
A.60°
B.45°
C.40°
D.30°
C
课堂精练
11. 如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45°
B.55°
C.60°
D.75°
C
课堂精练
已知△ABC是等边三角形,设AB,BC,AC边上的中线交于点G,∠BAC,∠ABC,∠ACB的平分线交于点I,AB,BC,AC边上的高交于点H,则下列结论:①点G与点I一定重合;②点G与点H一定重合;③点I与点H一定重合;④点G,点I与点H一定重合.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
易错点拨
因为等边三角形的三条边相等,所以等边三角形每条边上的中线、高与该边对角的平分线互相重合,所以点G,点I与点H一定重合.
易错点拨
1.等腰三角形的特殊性质:
(1)等腰三角形两底角的平分线相等;
(2)等腰三角形两腰上的高相等;
(3)等腰三角形两腰上的中线相等;
课堂小结
2.等边三角形的性质:
(1) 等边三角形的三边都相等;
(2) 等边三角形的三个内角都相等,并且每个角都等
于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分
别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长
度相等.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
