青岛版七年级数学下册 8.3角的度量 学案(含答案)
文档属性
| 名称 | 青岛版七年级数学下册 8.3角的度量 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 11:57:52 | ||
图片预览

文档简介
§8.3角的度量
【目标导航】
1.理解角的概念,学会角的表示方法;
2.认识角的度量单位度、分、秒,会进行简单的换算和角度计算;
3.会用量角器测一个角的大小,并借助三角板画出一些特殊角,会用尺规作一个角等于已知角,熟悉画法语言.
【预习引领】
观察发现:
⑴时钟的时针和分针,棱锥相交的两条棱,五角星的两条边给我们 的形象.
⑵这个图形是由什么基本图形构成的?
【要点梳理】
知识点一:角的概念及表示方法
1.静态定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线叫做角的边.
2.动态定义:一条射线绕着端点从一个位置旋转到另一个位置所形成的图形叫做角,起始位置称为角的始边,终止位置称为角的终边.射线旋转时覆盖的部分称为角的内部,其余部分称为角的外部.
3.角的表示方法:用符号“∠”,读作“角”.
⑴ ⑵ ⑶
⑴当顶点处只有一个角时,用一个字母表示,如“”;
⑵用三个大写字母表示,如“” ,其中A、B分别为两边上的任意点,O是顶点字母,要写在中间位置.;
⑶用阿拉伯字母或希腊字母表示, 如“” , “” .要在靠近顶点位置加上弧线,并注上数字或希腊字母.
例1 用适当的方法表示图1中的角.
图1 图2
⑴以O为顶点的角有 ;
⑵以D为顶点的角有 ;
⑶以E为顶点的角有 .
针对性练习:如图2:
⑴图中共有 个角;
⑵写出能用一个字母表示的角 ;
⑶写出以B为顶点的角 .
知识点二:角的度量
1.角度制:角的度量单位是度、分、秒,它们为60进制,即,.
角的度量制度还有弧度制.
2.特殊角:
1周角= ,1平角= ,
1直角= .
注:角的大小与边的长短无关,只与射线的张开幅度有关.
例2 填空
⑴平角= °,15°= 平角= 周角.
⑵91.28°=_____°_____′ ″;
3.32°=_____°_____′ ″.
例3 计算
⑴
⑵
⑶
⑷
知识点三:角的画法
1.用量角器可以画出任意给定角度的角.
2.借助三角尺,可以画出15°及其倍数的角.一副三角尺中的特殊角: .
3.尺规作图,可以画出一个角等于已知角.
例4 用一副三角尺画出下列角度的角.
⑴ 105° ⑵165°
例5 已知:,求作.
作法:⑴画一条 ;
⑵以O为圆心,任意长为半径画弧,交OA于点C,交OB于点D;
⑶以 为圆心, 长为半径画弧,交 _ 于点 ;
⑷以 为圆心, 长为半径画弧,交 于
⑸过点 画射线 ,则即为所求.
【课堂操练】
1.下列关于角的说法正确的个数是 ( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1个 B.2个 C.3个 D.4个
2.下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是 ( )
3.下列图中角的表示方法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4. 用一副三角板的内角可以画出大于0?但小于180?的不同角度的角共有 ( )
A.9种 B.10种 C.11种 D.12种
5.八点三十分,这一时刻,时针与分针夹角是 ( )
A.70° B.75° C.80° D.85°
6.从∠AOB的顶点O引出两条射线OC、OD两条射线,图中共有角的个数为 ( )
A.4个 B.5个 C.6个 D.7个
7.角的本质要点有两个:一是两条____,二是两条___ _;角的组成包括____,_____及角的内部,角不是射线,两条射线不一定组成角,角的大小与角的两边长短____.
8.用三个字母表示角时,必须把表示角的顶点的字母写在____.
9.角的单位――角度制是采用____进制.
10.当时钟的时间为6:30分时,时针与分针的夹角为 度.
11.从8点10分到8点40分,时钟的时针转过 度,时钟的分针转过 度.
12.108°42ˊ= °;
35.48°= 度 分 秒.
13.如果一个角是30°,用10倍的望远镜观察,这个角应是______°
14.30.6°=_____°_____′=_______′;
30°6′=_______′=______°.
15.计算:
⑴49°38′+66°22′
⑵180°-79°19′
⑶22°16′×5
⑷182°36′÷4
【课后盘点】
一、判断
?1.所有的直角都相等. ( ?)
2.大于直角的角都是钝角. ( ?)
?3. 由同一端点出发的两条直线组成的图形叫做角. ( )
?4.120.5°=120°50′. ( )
二、填空:
5.角是有公共端点的两条_______组成的图形,也可以看成是由一条___ ___绕?它的端点旋转而成的图形.____ __ ____叫做角的顶点,_ _____叫做角的始边,__ _____叫做?角的终边.
6.1周角=__ ___°;1平角=_ ___°;
7.18.32°=18° ″,
216°42′=_ __°.
8.若时钟表示的时间为5点15分时,时钟的时针和分针所成的锐角是 ___°.
9.13°39ˊ+64°45ˊ= ;
__ _______;
82°32′5″+ ____=180°.
三、选择
10.已知A、O、B三点,,则下列说法中,不正确的是 ( )
A. A、O、B三点共线
B.射线OA与射线OB共线
C.射线OA、OB互为反向延长线
D.
11.下列说法正确的是 ( )
A.角的两边可以度量;
B.角是由两条射线构成的图形.
C.一条直线可以看成是一个平角;
D.平角的两边可以看成直线.
12. 图中,小于平角的角有 ( )
A.5个 B.6个
C.7个 D.8个
13.下列各角中, ( ?)是钝角.
A.周角? B.?平角 C.平角? D.平角
14.用一副三角板的内角可以画出大于0°且小于176°的不同度数的角共有 (? )
?A.8种? B.9种 ?C.10种 ?D.11种
四、计算:
15.(1)36°54′+ 143°6′;
(2)50°20′36″+ 40°32′10″;
(3)90°-25°41′39″;
(4)180°-100°32′40″ ;
(5)25°40′5″×4;
(6)180°÷7(精确到分);
⑺;
16.根据下列语句画图:
(1)画∠AOB=100°;
(2)在∠AOB的内部画射线OC,∠BOC=50°;
(3)在∠AOB的外部画射线OD,∠DOA=40°;
(4)在射线OD上取E点,在射线OA上取F,使∠OEF=90°.
17.任意画一个三角形,估计其中三个角的度数,再用量角器检验你的估计是否准确.
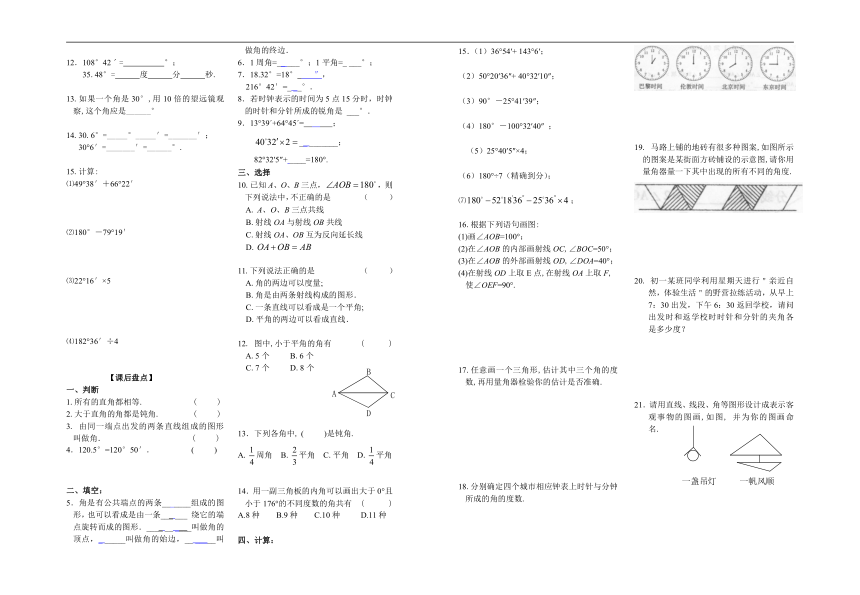
18.分别确定四个城市相应钟表上时针与分钟所成的角的度数.
19. 马路上铺的地砖有很多种图案,如图所示的图案是某街面方砖铺设的示意图,请你用量角器量一下其中出现的所有不同的角度.
20. 初一某班同学利用星期天进行"亲近自然,体验生活"的野营拉练活动,从早上7:30出发,下午6:30返回学校,请问出发时和返学校时时针和分针的夹角各是多少度?
21.请用直线、线段、角等图形设计成表示客观事物的图画,如图, 并为你的图画命名.
22.如果在∠AOD的内部从顶点O引出2条射线,求图中有多少个角?如果引出3条射线呢?如果引出100条射线呢?你发现了什么规律?
§8.3角的度量
参考答案:
知识点一:角的概念及表示方法
例1(1)答案:∠EOA, ∠EOB, ∠EOC, ∠AOB, ∠AOC, ∠BOC.
(2)答案:∠EOD, ∠CDF, ∠ODF, ∠EDC.
(3)答案:∠E
针对性练习:(1)答案:7
(2)答案: ∠A, ∠C
(3)答案:∠ABC, ∠ABD, ∠DBC
知识点二:角的度量
例2(1)答案:150°,,
(2)答案:91,16,48;3,19,12.
例3答案:(1)94°9_′
(2)64°27_′47″
(3)61°32_′32″
(4)21°32_′36″
知识点三:角的画法
例4解:(略)
例5(1)射线O′B′(3)O′,同样,O′B′,C′(4)C′,CD, 前弧, D′
(5) O′、D′, O′B′图(略)
【课堂操练】
1.A 2.B 3.B 4.C 5.B 6.C
7. 答案: 射线, 射线有公共端点,角的顶点,角的边,无关。
8. 答案:中间
9. 答案:六十
10. 答案:15
11. 答案:15,180
12. 答案:108.7,35,28,48
13. 答案:30
14. 答案:30,36,1836;1806,30.1
15.(1) 解:49°38′+66°22′
=116°
(2) 解:180°-79°19′
=100°41′
(3) 解:22°16′×5
=110°80′
=111°20′
(4) 解:182°36′÷4
=45°39
【课后盘点】
一、答案:1. √ 2. × 3. × 4. ×
二、5. 射线, 射线,射线的端点, 起始位置,终止位置
6.360,180
7. 19 ′12 ″,216.7
8. _67.5_
9. 78°24 ′,81°4,97°27′45″
三、10.B 11.D 12.D 13.B 14.D
四、15.(1)36°54′+ 143°6′
=180°
(2) 解:50°20′36″+ 40°32′10″
=90°52′46″
(3) 解:90°-25°41′39″
=64°18′21″
(4) 解:180°-100°32′40″
= 79°27′20″
(5) 解:25°40′5″×4
=100°160′20″
=102°40′20″
(6) 解:180°÷7
25°43′
(7) 解:;
=127°41′26″-102°24′
=25°17′26″
16. 解:(略)17解:(略)
18. 解:30°, 0°, 120 °,90°
19. 解:60°或120°
20. 解:出发时时针和分针的夹角是:45°
返学校时时针和分针的夹角是:15°
21. 解:(略)
22. 解:在∠AOD的内部从顶点O引出2条射线,图中有6个角;在∠AOD的内部从顶点O引出3条射线,求图中有10个角;在∠AOD的内部从顶点O引出100射线,图中有4950个角。
发现的规律:如果在∠AOD的内部从顶点O引出n条射线,则有个角
.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
