2020年北师大版初中数学七年级下学期《第2章 相交线与平行线》单元测试卷解析版
文档属性
| 名称 | 2020年北师大版初中数学七年级下学期《第2章 相交线与平行线》单元测试卷解析版 |
|
|
| 格式 | zip | ||
| 文件大小 | 121.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 00:00:00 | ||
图片预览




文档简介
北师大新版初中数学七年级下学期《第2章 相交线与平行线》2020年单元测试卷
一.选择题(共10小题)
1.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
2.如图,直线a,b相交于点O,若∠1等于30°,则∠2等于( )
A.60° B.70° C.150° D.170°
3.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
4.如图,AO⊥BO,垂足为点O,直线CD经过点O,下列结论正确的是( )
A.∠1+∠2=180° B.∠1﹣∠2=90° C.∠1﹣∠3=∠2 D.∠1+∠2=90°
5.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.两点之间,线段最短
B.垂线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
6.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;
③AB>AC>CD;④线段BC是B到AC的距离;⑤CD<BC<AB.
A.2个 B.3个 C.4个 D.5个
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则点B到直线CD的距离是指( )
A.线段BC的长度 B.线段CD的长度
C.线段AD的长度 D.线段BD的长度
8.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
9.下列各组线中一定互相垂直的是( )
A.对顶角的平分线 B.同位角的平分线
C.内错角的平分线 D.邻补角的平分线
10.如图,AB∥EF,设∠C=90°,那么x、y和z的关系是( )
A.y=x+z B.x+y﹣z=90° C.x+y+z=180° D.y+z﹣x=90°
二.填空题(共8小题)
11.如图,直线a、b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示138°的点在直线b上,则∠1= °.
12.已知一个角的两边分别垂直于另一个角的两边,且这两个角的差是30°,则这两个角的度数分别是 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
15.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .
16.如图,点D在△ABC的边AC的延长线上,DE∥BC,若∠A=65°,∠B=40°,则∠D的度数为 .
17.如图,若要说明AC∥DE,则可以添加的条件是 .
18.若∠A与∠B的两边分别平行,且∠A比∠B的5倍少20°,则∠A的度数为 .
三.解答题(共3小题)
19.直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,∠MGD+∠EAB=180°,MC平分∠AMG.
①∠AMG和∠EAB满足怎么样的数量关系时EC⊥AM?
②若∠AMG=36°,求∠ACD的度数.
20.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
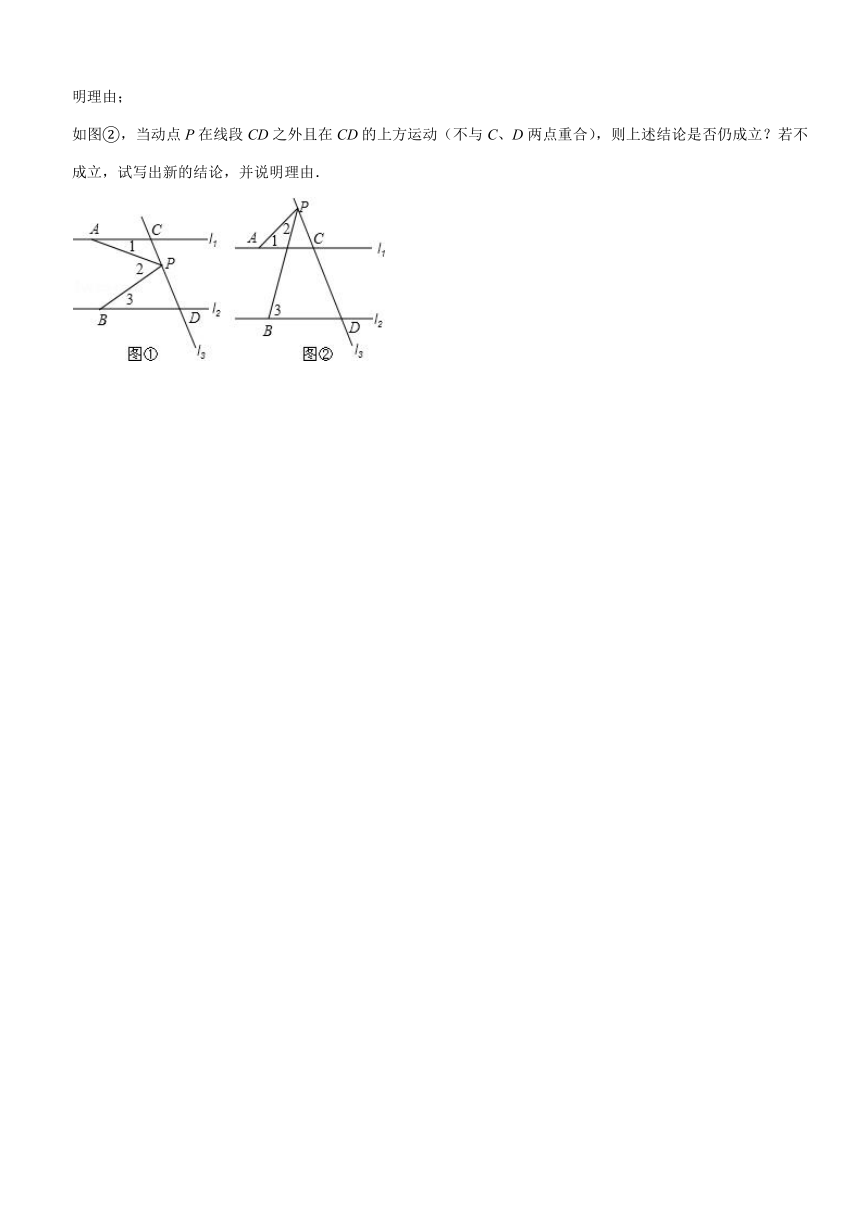
21.已知直线l1∥l2,直线l3与l1、l2分别交于C、D两点,点P是直线l3上的一动点,如图①,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有∠3+∠1=∠2这一相等关系?试说明理由;
如图②,当动点P在线段CD之外且在CD的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由.
北师大新版初中数学七年级下学期《第2章 相交线与平行线》2020年单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
2.【解答】解:∵∠1+∠2=180°,且∠1=30°,
∴∠2=150°.
故选:C.
3.【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.
故选:B.
4.【解答】解:∵如图,AO⊥BO,
∴∠AOB=90°.
A、∠1+∠3=180°,只有当∠2=∠3时,等式∠1+∠2=180°才成立,故本选项不符合题意.
B、∠1=180°﹣∠3,则∠1﹣∠2=180°﹣∠3﹣∠2=90°,故本选项符合题意.
C、∠1>90°,∠2+∠3=90°,则∠1≠∠3+∠2,即∠1﹣∠3=∠2,故本选项不符合题意.
D、∠2+∠3=90°,只有当∠1=∠3时,等式∠1+∠2=90°才成立,故本选项不符合题意.
故选:B.
5.【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故选:B.
6.【解答】解:①线段CD的长度是C点到AB的距离,正确;
②线段AC的长度是A点到BC的距离,错误;
③AB>AC>CD,正确;
④线段BC的长度是B到AC的距离,错误;
⑤CD<BC<AB,正确;
故选:B.
7.【解答】解:∵BD⊥CD于D,
∴点B到直线CD的距离是指线段BD的长度.
故选:D.
8.【解答】解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
9.【解答】解:A、对顶角的平分线在同一直线上,故本选项错误;
B、两条平行线被第三条直线所截,同位角的平分线互相平行,故本选项错误;
C、两条平行线被第三条直线所截,内错角的平分线互相平行,故本选项错误;
D、邻补角的平分线互相垂直,故本选项正确.
故选:D.
10.【解答】解:过C作CM∥AB,延长CD交EF于N,
则∠CDE=∠E+∠CNE,
即∠CNE=y﹣z
∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,
∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,
∴∠1+∠2=90°,
∴x+y﹣z=90°.
故选:B.
二.填空题(共8小题)
11.【解答】解:根据题意得:∠1=138°﹣60°=78°,
故答案为:78
12.【解答】解:∵一个角的两边分别垂直于另一个角的两边,
∴这两个角相等或互补.
又∵这两个角的差是30°,
∴这两个角互补.
设一个角为x,则另一个角为x+30°,
根据题意可知:x+x+30°=180°.
解得:x=75°,x+30°=75°+30°=105°.
故答案为:75°、105°.
13.【解答】解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.【解答】解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180°,
解得:x=20,
∴∠1=20°.
故答案为:20°.
15.【解答】解:用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是同位角相等,两直线平行;
故答案为:同位角相等,两直线平行.
16.【解答】解:如图所示:
∵∠A+∠B+∠ACB=180°,
∠A=65°,∠B=40°,
∴∠ACB=180°﹣∠A﹣∠B
=108°﹣65°﹣40°
=75°,
又∵DE∥BC,
∴∠ACB=∠D,
∴∠D=75°.
故答案为75°,
17.【解答】解:由题可得,当∠A=∠EDB时,AC∥DE,(同位角相等,两直线平行)
当∠A+∠ADE=180°时,AC∥DE,(同旁内角互补,两直线平行)
当∠C=∠CDE时,AC∥DE,(内错角相等,两直线平行)
故答案为:∠A=∠EDB(答案不唯一).
18.【解答】解:设∠B=x,则∠A=5x﹣20°,
由题意x=5x﹣20°,或x+5x﹣20°=180°,
解得x=5°或()°,
∴∠A=5°或()°
故答案为5°或()°.
三.解答题(共3小题)
19.【解答】解:(1)∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
∴∠BAC=180°﹣110°=70°,
又∵AM⊥EF,
∴∠MAN=90°﹣70°=20°;
(2)①当∠AMG=∠EAB=90°时EC⊥AM,理由如下:
∵CM是∠ACD的平分线,MC平分∠AMG,
∴∠ACM=∠GCM,∠AMC=∠GMC,
又∵CM=CM,
∴△AMC≌△GMC(ASA),
∴∠CGM=∠CAM,
∵EC⊥AM,
∴∠CGM=∠CAM=90°,
∴∠MGD=90°,
∵∠MGD+∠EAB=180°,
∴∠EAB=∠BAF=90°,
∵AB∥CD,
∴∠ACG=90°,
∴∠AMG=360°﹣90°﹣90°﹣90°=90°;
②∵MC平分∠AMG且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∴∠MCG=∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,则∠MCG=∠ACD=α,∠BAC=∠MGD=180°﹣α,
∵∠MGD是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即180°﹣α=α+18°,
解得α=108°,
∴∠ACD=108°.
20.【解答】证明:∵∠1=55°(已知),
∴∠CNM=55°(对顶角相等),
∵∠2=125°(已知),
∴∠CNM+∠2=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
21.【解答】解:(1)∠3+∠1=∠2成立,理由如下:
如图①,过点P作PE∥l1,
∴∠1=∠AEP,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2;
(2)∠3+∠1=∠2不成立,新的结论为∠3﹣∠1=∠2,理由为:
如图②,过P作PE∥l1,
∴∠1=∠APE,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE﹣∠APE=∠2,
∴∠3﹣∠1=∠2.
一.选择题(共10小题)
1.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
2.如图,直线a,b相交于点O,若∠1等于30°,则∠2等于( )
A.60° B.70° C.150° D.170°
3.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
4.如图,AO⊥BO,垂足为点O,直线CD经过点O,下列结论正确的是( )
A.∠1+∠2=180° B.∠1﹣∠2=90° C.∠1﹣∠3=∠2 D.∠1+∠2=90°
5.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.两点之间,线段最短
B.垂线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
6.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;
③AB>AC>CD;④线段BC是B到AC的距离;⑤CD<BC<AB.
A.2个 B.3个 C.4个 D.5个
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则点B到直线CD的距离是指( )
A.线段BC的长度 B.线段CD的长度
C.线段AD的长度 D.线段BD的长度
8.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
9.下列各组线中一定互相垂直的是( )
A.对顶角的平分线 B.同位角的平分线
C.内错角的平分线 D.邻补角的平分线
10.如图,AB∥EF,设∠C=90°,那么x、y和z的关系是( )
A.y=x+z B.x+y﹣z=90° C.x+y+z=180° D.y+z﹣x=90°
二.填空题(共8小题)
11.如图,直线a、b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示138°的点在直线b上,则∠1= °.
12.已知一个角的两边分别垂直于另一个角的两边,且这两个角的差是30°,则这两个角的度数分别是 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
15.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .
16.如图,点D在△ABC的边AC的延长线上,DE∥BC,若∠A=65°,∠B=40°,则∠D的度数为 .
17.如图,若要说明AC∥DE,则可以添加的条件是 .
18.若∠A与∠B的两边分别平行,且∠A比∠B的5倍少20°,则∠A的度数为 .
三.解答题(共3小题)
19.直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,∠MGD+∠EAB=180°,MC平分∠AMG.
①∠AMG和∠EAB满足怎么样的数量关系时EC⊥AM?
②若∠AMG=36°,求∠ACD的度数.
20.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
21.已知直线l1∥l2,直线l3与l1、l2分别交于C、D两点,点P是直线l3上的一动点,如图①,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有∠3+∠1=∠2这一相等关系?试说明理由;
如图②,当动点P在线段CD之外且在CD的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由.
北师大新版初中数学七年级下学期《第2章 相交线与平行线》2020年单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
2.【解答】解:∵∠1+∠2=180°,且∠1=30°,
∴∠2=150°.
故选:C.
3.【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.
故选:B.
4.【解答】解:∵如图,AO⊥BO,
∴∠AOB=90°.
A、∠1+∠3=180°,只有当∠2=∠3时,等式∠1+∠2=180°才成立,故本选项不符合题意.
B、∠1=180°﹣∠3,则∠1﹣∠2=180°﹣∠3﹣∠2=90°,故本选项符合题意.
C、∠1>90°,∠2+∠3=90°,则∠1≠∠3+∠2,即∠1﹣∠3=∠2,故本选项不符合题意.
D、∠2+∠3=90°,只有当∠1=∠3时,等式∠1+∠2=90°才成立,故本选项不符合题意.
故选:B.
5.【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故选:B.
6.【解答】解:①线段CD的长度是C点到AB的距离,正确;
②线段AC的长度是A点到BC的距离,错误;
③AB>AC>CD,正确;
④线段BC的长度是B到AC的距离,错误;
⑤CD<BC<AB,正确;
故选:B.
7.【解答】解:∵BD⊥CD于D,
∴点B到直线CD的距离是指线段BD的长度.
故选:D.
8.【解答】解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
9.【解答】解:A、对顶角的平分线在同一直线上,故本选项错误;
B、两条平行线被第三条直线所截,同位角的平分线互相平行,故本选项错误;
C、两条平行线被第三条直线所截,内错角的平分线互相平行,故本选项错误;
D、邻补角的平分线互相垂直,故本选项正确.
故选:D.
10.【解答】解:过C作CM∥AB,延长CD交EF于N,
则∠CDE=∠E+∠CNE,
即∠CNE=y﹣z
∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,
∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,
∴∠1+∠2=90°,
∴x+y﹣z=90°.
故选:B.
二.填空题(共8小题)
11.【解答】解:根据题意得:∠1=138°﹣60°=78°,
故答案为:78
12.【解答】解:∵一个角的两边分别垂直于另一个角的两边,
∴这两个角相等或互补.
又∵这两个角的差是30°,
∴这两个角互补.
设一个角为x,则另一个角为x+30°,
根据题意可知:x+x+30°=180°.
解得:x=75°,x+30°=75°+30°=105°.
故答案为:75°、105°.
13.【解答】解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.【解答】解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180°,
解得:x=20,
∴∠1=20°.
故答案为:20°.
15.【解答】解:用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是同位角相等,两直线平行;
故答案为:同位角相等,两直线平行.
16.【解答】解:如图所示:
∵∠A+∠B+∠ACB=180°,
∠A=65°,∠B=40°,
∴∠ACB=180°﹣∠A﹣∠B
=108°﹣65°﹣40°
=75°,
又∵DE∥BC,
∴∠ACB=∠D,
∴∠D=75°.
故答案为75°,
17.【解答】解:由题可得,当∠A=∠EDB时,AC∥DE,(同位角相等,两直线平行)
当∠A+∠ADE=180°时,AC∥DE,(同旁内角互补,两直线平行)
当∠C=∠CDE时,AC∥DE,(内错角相等,两直线平行)
故答案为:∠A=∠EDB(答案不唯一).
18.【解答】解:设∠B=x,则∠A=5x﹣20°,
由题意x=5x﹣20°,或x+5x﹣20°=180°,
解得x=5°或()°,
∴∠A=5°或()°
故答案为5°或()°.
三.解答题(共3小题)
19.【解答】解:(1)∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
∴∠BAC=180°﹣110°=70°,
又∵AM⊥EF,
∴∠MAN=90°﹣70°=20°;
(2)①当∠AMG=∠EAB=90°时EC⊥AM,理由如下:
∵CM是∠ACD的平分线,MC平分∠AMG,
∴∠ACM=∠GCM,∠AMC=∠GMC,
又∵CM=CM,
∴△AMC≌△GMC(ASA),
∴∠CGM=∠CAM,
∵EC⊥AM,
∴∠CGM=∠CAM=90°,
∴∠MGD=90°,
∵∠MGD+∠EAB=180°,
∴∠EAB=∠BAF=90°,
∵AB∥CD,
∴∠ACG=90°,
∴∠AMG=360°﹣90°﹣90°﹣90°=90°;
②∵MC平分∠AMG且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∴∠MCG=∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,则∠MCG=∠ACD=α,∠BAC=∠MGD=180°﹣α,
∵∠MGD是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即180°﹣α=α+18°,
解得α=108°,
∴∠ACD=108°.
20.【解答】证明:∵∠1=55°(已知),
∴∠CNM=55°(对顶角相等),
∵∠2=125°(已知),
∴∠CNM+∠2=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
21.【解答】解:(1)∠3+∠1=∠2成立,理由如下:
如图①,过点P作PE∥l1,
∴∠1=∠AEP,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2;
(2)∠3+∠1=∠2不成立,新的结论为∠3﹣∠1=∠2,理由为:
如图②,过P作PE∥l1,
∴∠1=∠APE,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE﹣∠APE=∠2,
∴∠3﹣∠1=∠2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
