苏教版高中数学必修四第三章第一节《两角和与差的余弦》课件(共15张PPT)
文档属性
| 名称 | 苏教版高中数学必修四第三章第一节《两角和与差的余弦》课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第三章
三角恒等变换
§3.1.1两角和与差的余弦
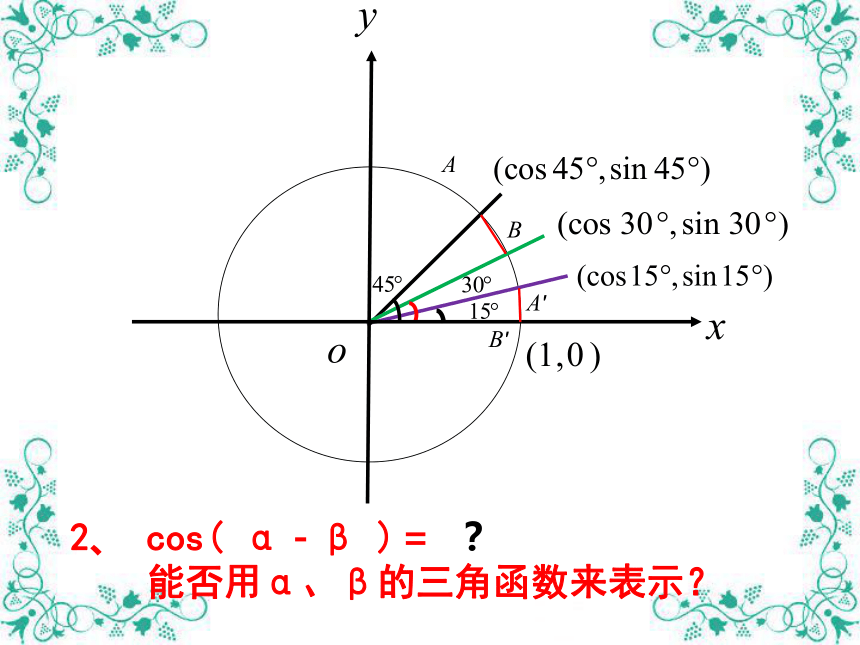
2、 cos( α-β )= ?
能否用α、β的三角函数来表示?
单位圆上的点的坐标表示
两角差的余弦公式
结
论
归
纳
【问】:根据两角差的余弦公式,我们可以猜猜
公式特征: 1.公式中两边的符号正好相反(一正一负)
2.式子右边同名三角函数相乘再加减,且
余弦在前正弦在后
3.式子中α、β是任意的
4.式子的逆用,变形用
1、请用特殊角分别代替公式中α、β,你能求哪些非特殊角的值呢?cos15°、cos75°、sin15°、tan15°?
说明:两角和与差的余弦公式可以将非特
殊角余弦转化为特殊角的余弦去求解。
若β固定,分别用
代替α,你将会发现什么结论呢?
2、
说明:特殊角度起到了化简的作用,诱导公式本质是特殊的两角和与差的余弦公式.
说明:是公式的逆用,注意公式结构
3、(1)求 cos80°cos20°+sin80°sin20°的值
(3)求cos?15°-sin?15° 的值
(2)求 cos15°sin75°-sin15°cos75°的值
解:原式= cos15°sin(90°-15°)-sin15°cos(90°-15°)
= cos15°cos15°-sin15°sin15°
解:原式=cos(15°+15°)=cos30°=
注意:任意角α、β的象限,也就是三角函数符号问题.
例2、已知
解:由 知
由余弦的差角公式得
公式的推导与记忆
如何根据条件与结论的关系对公式中的角进行分解、
组合和代换。
(1)计算三角值,用特殊角表示非特殊角
(2)更一般的用已知角表示未知角
(3)公式的正用求三角函数值和逆用公式进行化简。
第三章
三角恒等变换
§3.1.1两角和与差的余弦
2、 cos( α-β )= ?
能否用α、β的三角函数来表示?
单位圆上的点的坐标表示
两角差的余弦公式
结
论
归
纳
【问】:根据两角差的余弦公式,我们可以猜猜
公式特征: 1.公式中两边的符号正好相反(一正一负)
2.式子右边同名三角函数相乘再加减,且
余弦在前正弦在后
3.式子中α、β是任意的
4.式子的逆用,变形用
1、请用特殊角分别代替公式中α、β,你能求哪些非特殊角的值呢?cos15°、cos75°、sin15°、tan15°?
说明:两角和与差的余弦公式可以将非特
殊角余弦转化为特殊角的余弦去求解。
若β固定,分别用
代替α,你将会发现什么结论呢?
2、
说明:特殊角度起到了化简的作用,诱导公式本质是特殊的两角和与差的余弦公式.
说明:是公式的逆用,注意公式结构
3、(1)求 cos80°cos20°+sin80°sin20°的值
(3)求cos?15°-sin?15° 的值
(2)求 cos15°sin75°-sin15°cos75°的值
解:原式= cos15°sin(90°-15°)-sin15°cos(90°-15°)
= cos15°cos15°-sin15°sin15°
解:原式=cos(15°+15°)=cos30°=
注意:任意角α、β的象限,也就是三角函数符号问题.
例2、已知
解:由 知
由余弦的差角公式得
公式的推导与记忆
如何根据条件与结论的关系对公式中的角进行分解、
组合和代换。
(1)计算三角值,用特殊角表示非特殊角
(2)更一般的用已知角表示未知角
(3)公式的正用求三角函数值和逆用公式进行化简。
