必修4第一章《三角函数》期末复习课件
文档属性
| 名称 | 必修4第一章《三角函数》期末复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
第一章 三角函数
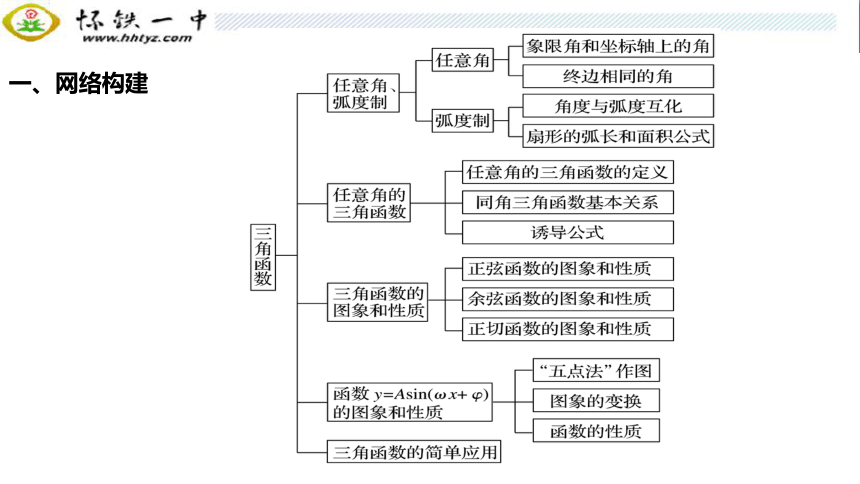
一、网络构建
二、要点归纳
1.任意角三角函数的定义
在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的 ,记作 ,即 .
(2)x叫做α的 ,记作 ,即 .
(3) 叫做α的 ,记作 ,即 .
2.同角三角函数的基本关系式
(1)平方关系: .
(2)商数关系:tan α=
正弦
sin α
sin α=y
余弦
cos α
cos α=x
正切
tan α
sin2α+cos2α=1
3.诱导公式
一、函数名不变,符号看象限
二、函数名互余,符号看象限
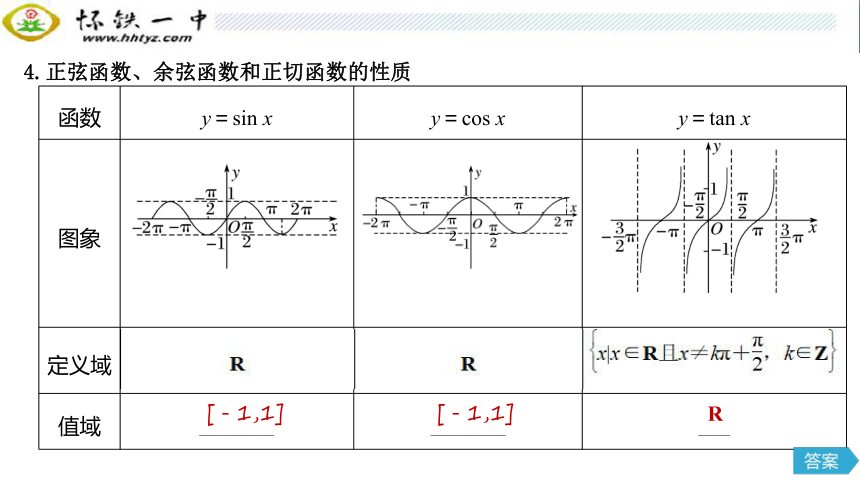
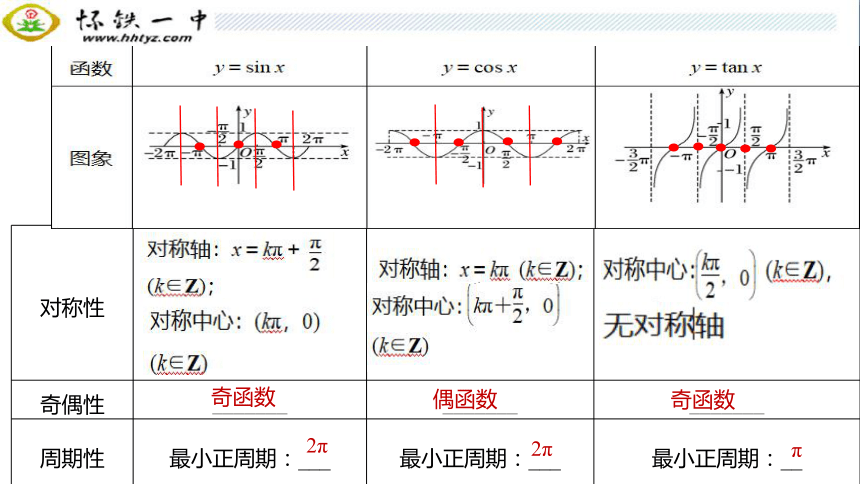
4.正弦函数、余弦函数和正切函数的性质
[-1,1]
[-1,1]
R
函数 y=sin x y=cos x y=tan x
图象
定义域
值域 _______ _______ ___
奇函数
偶函数
奇函数
2π
2π
π
对称性
奇偶性 _______ _______ _______
周期性 最小正周期:___ 最小正周期:___ 最小正周期:__
2
题型探究
PART TWO
题型一 三角函数的化简与求值
(1)化简f(α);
(cos α-sin α)2=cos2α-2sin α·cos α+sin2α
解决三角函数的化简与求值问题一般先化简再求值.在应用中,要注意掌握解题的技巧.比如:已知sin α±cos α的值,可求cos αsin α,注意应用(cos α±sin α)2=1±2sin αcos α.
(1)求tan α的值;
因为α是三角形的内角,所以sin α>0,cos α<0,
题型二 三角函数的图象与性质
(1)写出f(x)的最小正周期及图中x0,y0的值;
研究y=Asin(ωx+φ)的单调性、最值问题,把ωx+φ看作一个整体来解决.
2sin(2×π+φ)=2sin φ=-1,
题型三 三角函数的最值或值域
命题角度1 可化为y=Asin(ωx+φ)+k型
多维探究
利用y=Asin(ωx+φ)+k求值域时要注意角的取值范围对函数式取值的影响.
√
故选A.
命题角度2 可化为二次函数型
[-4,4]
令tan x=t,则t∈[-1,1],
∴y=-t2+4t+1=-(t-2)2+5.
故所求函数的值域为[-4,4].
在换元时要立刻写出新元的范围,否则极易出错.
1
题型四 数形结合思想在三角函数中的应用
解 sin2x-(2+a)sin x+2a=0,
即(sin x-2)(sin x-a)=0.
∵sin x-2≠0,∴sin x=a,
数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图象时,常利用数形结合思想.
A.4 B.5 C.6 D.7
当x>0时,两函数图象如图所示,
两图象有3个公共点,
同理,当x<0时,两图象也有3个公共点,
故两图象共有6个公共点,从而方程有6个实数根,
故选C.
√
3
达标检测
PART THREE
√
1
2
3
4
5
1
2
3
4
5
√
√
1
2
3
4
5
解析 平移后的图象对应的函数为
因为此函数为偶函数,
1
2
3
4
5
A.2 B.-2 C.1 D.-1
√
1
2
3
4
5
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
1
2
3
4
5
1
2
3
4
5
所以当x=0时,f(x)取得最小值,
(2)求函数f(x)在区间[-2,-1]上的最值.
任取x1,x2∈[-2,-1],且x1∵-2≤x1∴x1-x2<0,x1x2>1,x1x2-1>0,
∴f(x1)-f(x2)<0,即f(x1)∴函数f(x)在[-2,-1]上为增函数.
爱生活,爱数学!
第一章 三角函数
一、网络构建
二、要点归纳
1.任意角三角函数的定义
在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的 ,记作 ,即 .
(2)x叫做α的 ,记作 ,即 .
(3) 叫做α的 ,记作 ,即 .
2.同角三角函数的基本关系式
(1)平方关系: .
(2)商数关系:tan α=
正弦
sin α
sin α=y
余弦
cos α
cos α=x
正切
tan α
sin2α+cos2α=1
3.诱导公式
一、函数名不变,符号看象限
二、函数名互余,符号看象限
4.正弦函数、余弦函数和正切函数的性质
[-1,1]
[-1,1]
R
函数 y=sin x y=cos x y=tan x
图象
定义域
值域 _______ _______ ___
奇函数
偶函数
奇函数
2π
2π
π
对称性
奇偶性 _______ _______ _______
周期性 最小正周期:___ 最小正周期:___ 最小正周期:__
2
题型探究
PART TWO
题型一 三角函数的化简与求值
(1)化简f(α);
(cos α-sin α)2=cos2α-2sin α·cos α+sin2α
解决三角函数的化简与求值问题一般先化简再求值.在应用中,要注意掌握解题的技巧.比如:已知sin α±cos α的值,可求cos αsin α,注意应用(cos α±sin α)2=1±2sin αcos α.
(1)求tan α的值;
因为α是三角形的内角,所以sin α>0,cos α<0,
题型二 三角函数的图象与性质
(1)写出f(x)的最小正周期及图中x0,y0的值;
研究y=Asin(ωx+φ)的单调性、最值问题,把ωx+φ看作一个整体来解决.
2sin(2×π+φ)=2sin φ=-1,
题型三 三角函数的最值或值域
命题角度1 可化为y=Asin(ωx+φ)+k型
多维探究
利用y=Asin(ωx+φ)+k求值域时要注意角的取值范围对函数式取值的影响.
√
故选A.
命题角度2 可化为二次函数型
[-4,4]
令tan x=t,则t∈[-1,1],
∴y=-t2+4t+1=-(t-2)2+5.
故所求函数的值域为[-4,4].
在换元时要立刻写出新元的范围,否则极易出错.
1
题型四 数形结合思想在三角函数中的应用
解 sin2x-(2+a)sin x+2a=0,
即(sin x-2)(sin x-a)=0.
∵sin x-2≠0,∴sin x=a,
数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图象时,常利用数形结合思想.
A.4 B.5 C.6 D.7
当x>0时,两函数图象如图所示,
两图象有3个公共点,
同理,当x<0时,两图象也有3个公共点,
故两图象共有6个公共点,从而方程有6个实数根,
故选C.
√
3
达标检测
PART THREE
√
1
2
3
4
5
1
2
3
4
5
√
√
1
2
3
4
5
解析 平移后的图象对应的函数为
因为此函数为偶函数,
1
2
3
4
5
A.2 B.-2 C.1 D.-1
√
1
2
3
4
5
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
1
2
3
4
5
1
2
3
4
5
所以当x=0时,f(x)取得最小值,
(2)求函数f(x)在区间[-2,-1]上的最值.
任取x1,x2∈[-2,-1],且x1
∴f(x1)-f(x2)<0,即f(x1)
爱生活,爱数学!
