5.1 相交线同步练习（含解析）

中小学教育资源及组卷应用平台


人教版2019-2020学年七年级数学下学期5.1相交线
（时间60分钟 总分100分）
一、选择题（每小题5分，共30分）
1.下列各图中，∠1与∠2互为邻补角的是（ ）
A. B. C. D.
2.如图，，直线BD经过点0，且，则∠COD的度数为（ ）

A.70° B.110° C.140° D.160°
3.点P为直线l外一点，点A，B，C为直线l上三点，PA=2cm，PB=3cm，PC=4cm，则点P到直线l的距离（ ）
A.等于2cm B.小于2cm C.大于2cm D.不大于2cm
4.如图，三条直线相交于一点，则∠1+∠2+∠3等于（ ）

A. B. C. D.
5.如图，，下列结论中，正确的结论有（ ）
①线段CD的长度是点C到AB的距离；②线段AC是点A到BC的距离；③AB>AC>CD；④线段BC是点B到AC的距离；⑤CD
A.2个 B.3个 C.4个 D.5个
6.如图，给出下列四个结论：
①∠2与∠6是内错角；②∠3与∠4是内错角；
③∠5与∠6是同旁内角；④∠1与∠4是同旁内角.
其中正确的是（ ）

A.①② B.②③④ C.①②④ D.①②③④

二、填空题（每小题5分，共20分）
7.如图所示，在直角三角形ABC中，，过点A作，垂足为D，已知AB=6cm，AD=5cm.

（1）点B到AC的距离为______，点A到BC的距离为______；
（2）CD______AC（填“>“<”或“=”），依据是.
8.如图，填空：

（1）∠1和∠B是直线______，______被直线______所截形成的角；
（2）∠2和∠A是直线______，______被直线______所截形成的角；
（3）∠B和∠ECB是直线______，______被直线______所截形成的角.
9.如图，，若∠AOD=150°，则∠BOC的度数是_______

10.如图（1），两条直线相交所组成的角中，互为对顶角的角有两对：∠AOD和∠COB，
∠AOC和∠BOD.
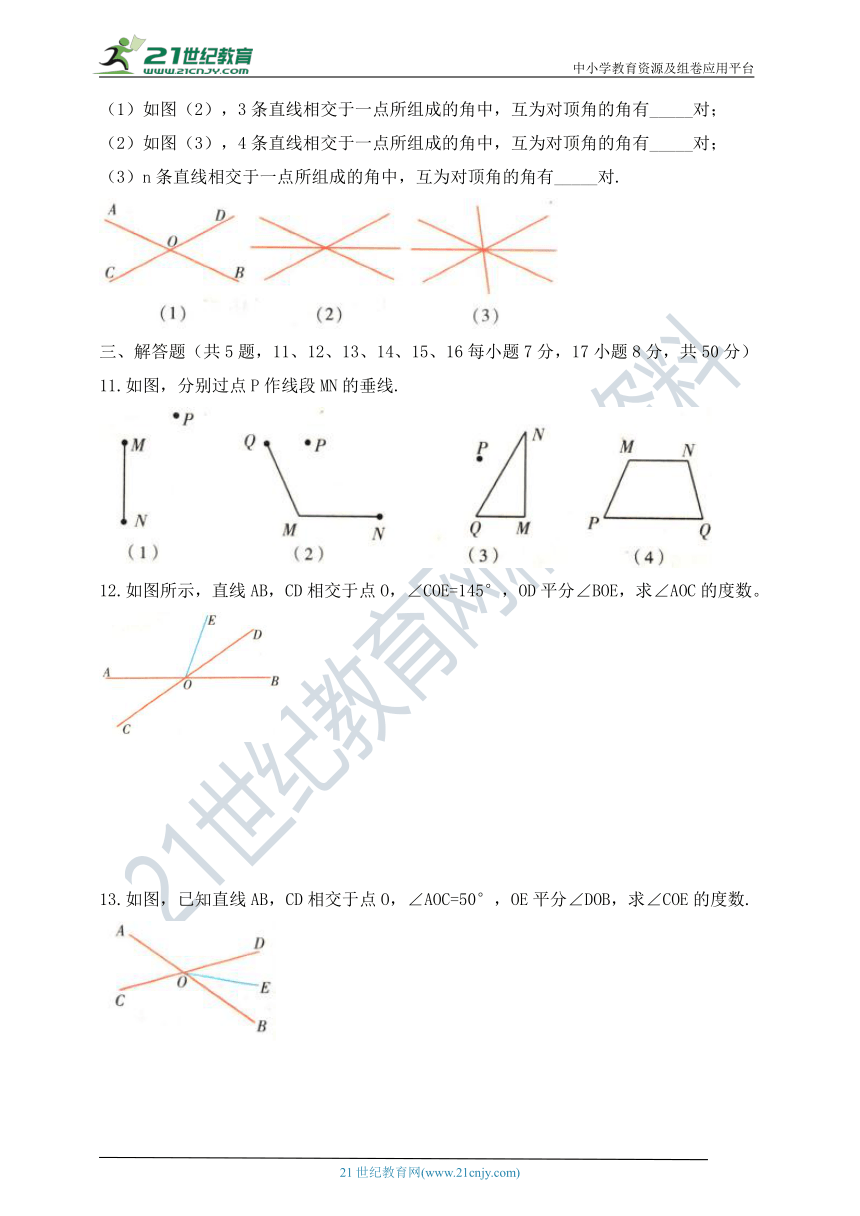
（1）如图（2），3条直线相交于一点所组成的角中，互为对顶角的角有_____对；
（2）如图（3），4条直线相交于一点所组成的角中，互为对顶角的角有_____对；
（3）n条直线相交于一点所组成的角中，互为对顶角的角有_____对.

三、解答题（共5题，11、12、13、14、15、16每小题7分，17小题8分，共50分）
11.如图，分别过点P作线段MN的垂线.

12.如图所示，直线AB，CD相交于点O，∠COE=145°，OD平分∠BOE，求∠AOC的度数。





13.如图，已知直线AB，CD相交于点O，∠AOC=50°，OE平分∠DOB，求∠COE的度数.




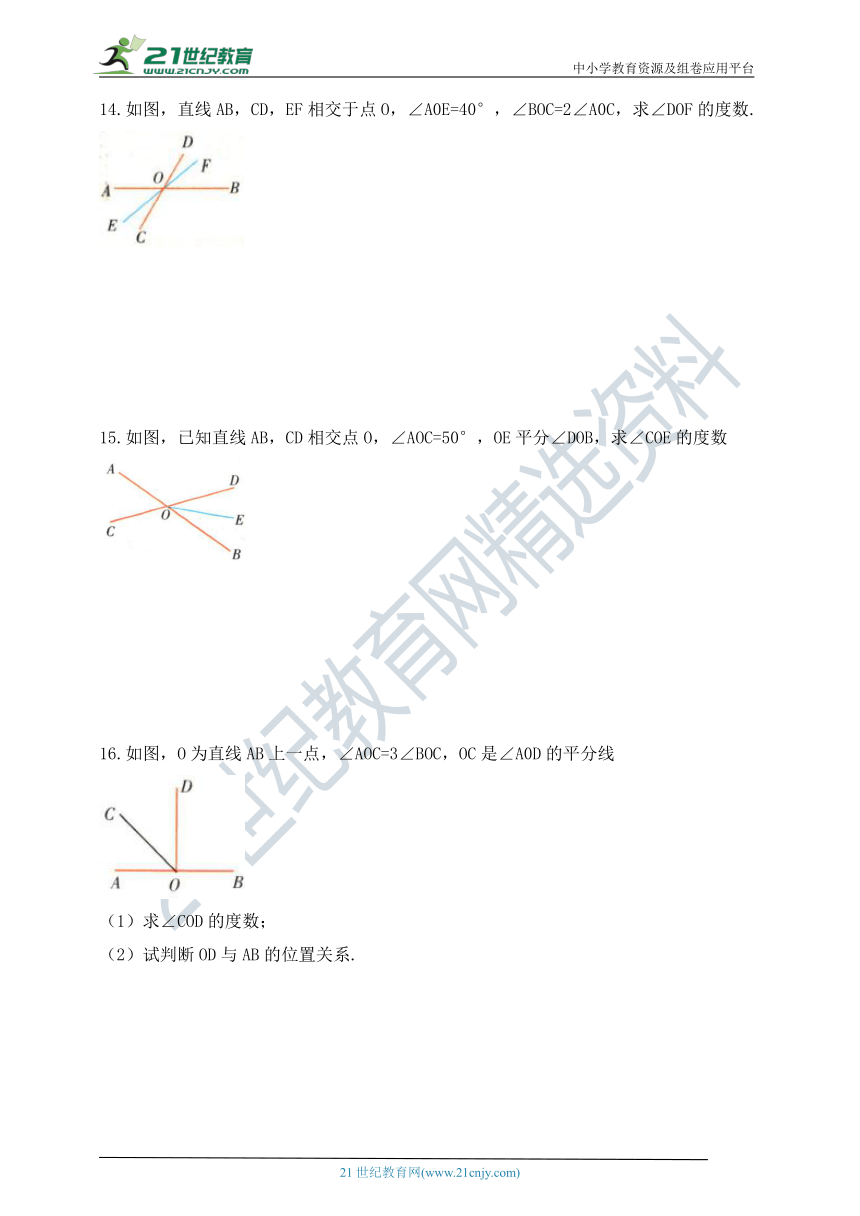
14.如图，直线AB，CD，EF相交于点O，∠A0E=40°，∠BOC=2∠A0C，求∠DOF的度数.






15.如图，已知直线AB，CD相交点O，∠AOC=50°，OE平分∠DOB，求∠COE的度数






16.如图，O为直线AB上一点，∠AOC=3∠BOC，OC是∠A0D的平分线

（1）求∠COD的度数；
（2）试判断OD与AB的位置关系.





17.如图，直线AB，CD相交于点O，OE是∠COB的平分线，FOLOE于点0，已知
∠AOD=70°.

（1）求∠BOE的度数；
（2）OF平分∠AOC吗？为什么？



















答案
1.【解析】根据邻补角的定义可知，只有选项D中的∠1与∠2互为邻补角.
答案：D
2.【解析】因为，所以∠AOC=90°.因为∠1=20°，所以∠COB=70°，所以∠COD=180°-70°=110°.
答案：B
3.【解析】当时，点P到直线l的距离为PA=2cm；当PA与l不垂直时，点P到直线l的距离小于PA.综上可知，点P到直线l的距离不大于2cm.
答案：D
4.【解析】因为∠2的对顶角与∠1，∠3的和正好等于180°，根据对顶角相等，得∠1+∠2+∠3=180°.
答案：C
5.【解析】线段CD的长度是点C到AB的距离，故①正确；线段AC的长度是点A到BC的距离，故②错误；AB>AC>CD，故③正确；线段BC的长度是点B到AC的距离，故
④错误；CD答案：B
6.【解析】∠2与∠6是直线DF，DC被直线AB所截形成的内错角，故①正确；∠3与∠4是直线AB，AC被直线DF所截形成的内错角，故②正确；根据同旁内角的定义可知∠5与∠6不是同旁内角，故③不正确；∠1与∠4是直线AB，AC被直线DF所截形成的同旁内角，故④正确。故选C.
答案：C
7.【解析】（1）点B到AC的距离为线段AB的长度，为6cm；点A到BC的距离为线段AD的长度，为5cm.
（2）CD是点C到AD的垂线段，根据垂线段最短，可知CD8.【解析】（1）∠1和∠B都有一条边落在直线BD上，则BD为截线，另两条边所在的直线EC和AB是被截直线，由同位角的定义可知∠1和∠B是同位角.
（2）∠2和∠A都有一条边落在直线AC上，则AC为截线，另两条边所在的直线EC和AB是被截直线，由内错角的定义可知∠2和∠A是内错角.
（3）∠B和∠ECB都有一条边落在直线BD上，则BD为截线，另两条边所在的直线AB和EC是被截直线，由同旁内角的定义可知∠B和∠ECB是同旁内角
9.【解析】因为，所以∠AOC=∠DOB=90°，所以∠BOC=∠AOC+∠DOB-∠AOD=180°-150°=30°.
10.【解析】3条直线两两配对，形成了3个“又”，每个“叉”中有2对对顶角，所以互为对顶角的角有6对.
4条直线两两配对，形成了6个“叉”，所以互为对顶角的角有12对
n条直线两两配对，共有个“又”，所以互为对顶角的角有n（n-1）对
11.【解析】

12.【解析】解析，因为∠COE=145°，所以∠DOE=180°-∠COE=180°-145°=35°.
因为OD平分∠BOE，所以∠BOD=∠DOE=35°，所以∠AOC=∠BOD=35°.
13.【解析】因为∠AOC=50°，所以∠COB=180°-∠AOC=130°，∠DOB=∠AOC=50°.
因为OE平分∠DOB，所以∠BOE=∠B0D=25°，所以∠COE=∠COB+∠B0E=130°+250=155°.
14.【解析】设∠AOC=x，则∠BOC=2x.由邻补角的性质可得x+2x=180°，解得x=60°，即∠A0C=60°，所以∠EOC=∠A0C-∠A0E=60°-40°=20°，由对顶角相等得∠DOF=∠EOC=20°.
15.【解析】因为∠AOC=50°，所以∠COB=180°-∠AOC=130°，∠DOB=∠AOC=50°.
因为OE平分∠DOB，所以∠BOE=-∠BOD=25°，所以∠COE=∠COB+∠BOE=130°+25°=155°.
16.【解析】（1）设∠AOC=x°，因为OC是∠AOD的平分线，所以∠COD=∠AOC=x°.
因为∠AOC=-∠B0C，所以∠BOC=3∠AOC=3x°.因为∠A0C+∠BOC=180°，所以x+3x=180，所以x=45，所以∠COD=x°=45°.
（2）因为∠A0D=∠AOC+∠COD=90°，所以.
17.【解析】（1）根据对顶角相等，得∠BOC=∠AOD=70°.因为OE是∠BOC的平分线，所以∠B0E=-∠BOC=35°
（2）OF平分∠AOC.理由如下：因为∠AOD=70°，所以∠AOC=180°-∠AOD=180°-70°=110°，又∠FOC=∠FOE-∠COE=90°-350=55°，所以∠FOC=∠F0A=∠AOC，所以OF平分∠AOC.







21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)