北师大版七年级数学下册4.3 探索三角形全等的条件课件(第1课时)(31张PPT)
文档属性
| 名称 | 北师大版七年级数学下册4.3 探索三角形全等的条件课件(第1课时)(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 17:10:02 | ||
图片预览








文档简介
(共31张PPT)
北师大七年级数学下册
第四章 三角形
3 探索三角形全等的条件(第1课时)
教学目标
1、经历探索三角形全等条件的过程,体会利用
操作、归纳得出数学结论的过程;在探索三角
形全等条件及应用的过程中,能够进行有条理
的思考,并能进行简单的推理。
2、掌握三角形全等的 “边边边”(“SSS”)条
件,并能利用这些条件判别两个三角形是否全
等。
3、了解三角形的稳定性及其在生活中的应用。
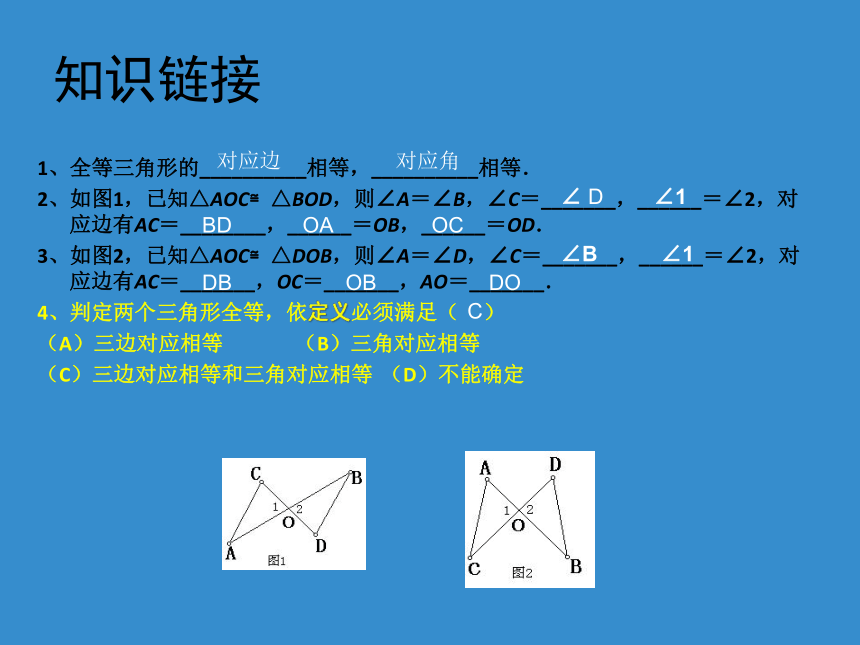
知识链接
1、全等三角形的__________相等,__________相等.
2、如图1,已知△AOC≌△BOD,则∠A=∠B,∠C=_______,______=∠2,对应边有AC=________,______=OB,______=OD.
3、如图2,已知△AOC≌△DOB,则∠A=∠D,∠C=_______,______=∠2,对应边有AC=_______,OC=_______,AO=_______.
4、判定两个三角形全等,依定义必须满足( )
(A)三边对应相等 (B)三角对应相等
(C)三边对应相等和三角对应相等 (D)不能确定
对应边
对应角
∠ D
∠1
BD
OA
OC
∠B
∠1
DB
OB
DO
C
新知探究
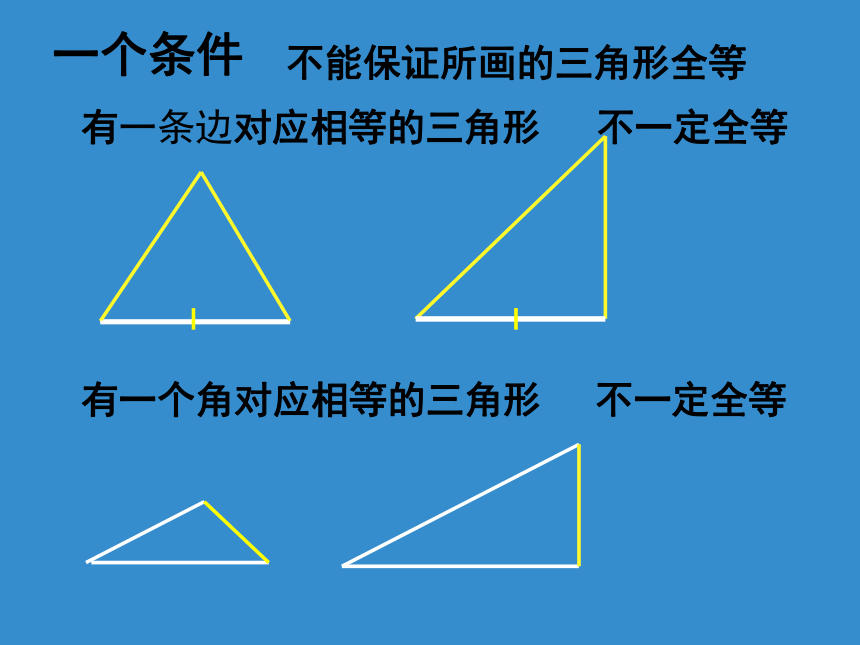
提出问题:我们知道能够完全重合的两个三角形叫做全等三角形。那么判断两个三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?…….
动手操作问题一:
1. 只给一个条件画三角形,这个条件可以是_________,画一画,大家画出的三角形一定全等吗?
一条边或一个角
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
给出两个条件画三角形,有几种可能的情况?画一画,大家画出的三角形全等吗?
1、一边和一角
2、两个角
3、两条边
动手操作问题二:
分别按照下面的条件做一做。
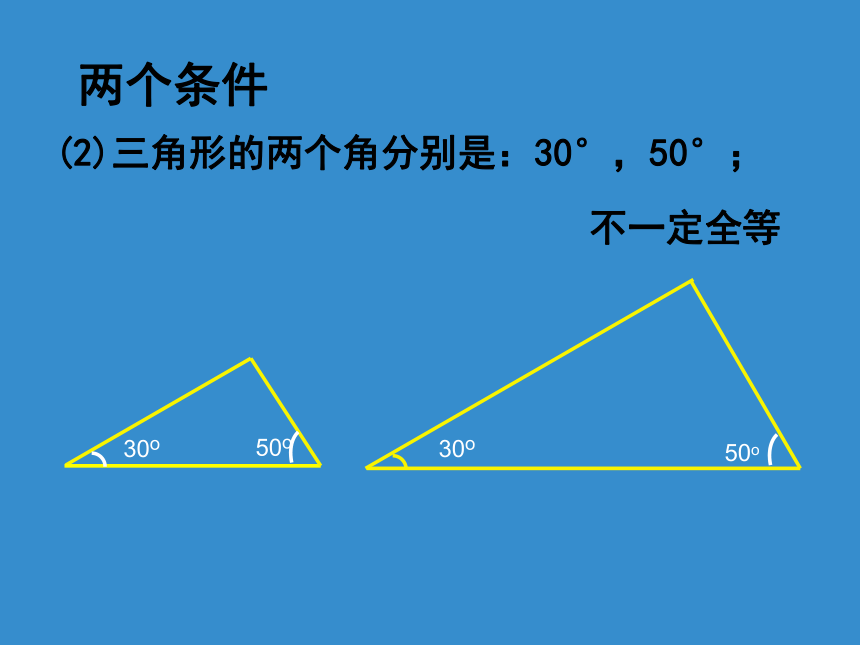
两个条件
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个角为30°,一条边为3cm;
不一定全等
两个条件
30o
3cm
30o
3cm
(2)三角形的两个角分别是:30°,50°;
不一定全等
50o
两个条件
50o
30o
30o
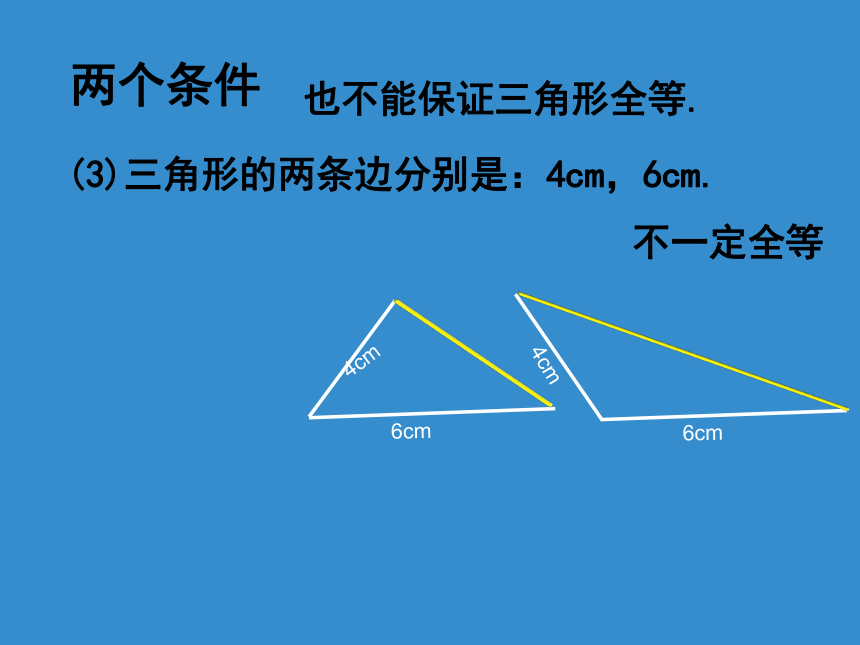
(3)三角形的两条边分别是:4cm,6cm.
不一定全等
6cm
4cm
也不能保证三角形全等.
两个条件
4cm
6cm
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
动手操作问题一二总结:
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
不一定全等
动手操作问题三:
只给一个条件,或只给两个条件,都不能保证画出的三角形一定全等,那么如果给出三个条件画三角形呢?你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
三个条件
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角分别相等的两个三角形不一定全等
三个条件
(2) 给出长度分别为4cm,5cm和7cm的木棒,你能摆出这个三角形吗?把你摆的三角形与同伴摆出的进行比较,它们一定全等吗?
三边分别相等的两个三角形全等
三角形全等判定方法1.
三边分别相等的两个三角形全等。 简写成“边边边”或“SSS”
AB=DE
AC= DF
BC= EF
(SSS)
D
E
F
A
B
C
在△ABC和△DEF中
ABC ≌ DEF
所以
用符号语言表达为:
如右图在四边形ACBD中,AC=AD,BD=BC,则∠C=∠D,请说明理由
例1
A
B
C
D
解:在△ABC与△ABD中
AB= ( )
∵ AC= ( )
=BD ( )
∴△ABC≌ △ABD ( )
∴∠C=∠D ( )
公共边
已知
已知
全等三角形的对应角相等
SSS
AB
AD
BC
变式:已知:如图,AC=AD,BD=BC
求证:AB平分∠ DAC
A
D
B
C
动手操作四:
准备几根硬纸条
(1)取出三根木棒钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根木棒钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?
(3)上面的现象说明了什么?
用三根木棒钉成的一个三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。用四根木棒钉成的框架它的形状是可以改变的,因此,四边形具有不稳定性。
思考:你有办法使四边形的框架的形状不发生变化吗?
图片欣赏
你能说出为什么这些地方是三角形吗?
说说看你有什么收获?
1. 三角形全等的条件:
2. 三角形具有稳定性。
达标测评
1. 两个锐角对应相等的两个直角三角形全等吗?为什么?
不一定全等
解:
A
B
C
D
E
F
RtΔABC和RtΔDEF不全等
2、如图,ΔABC中,AB=AC,BE=EC,则由“SSS”可判定…………………………( )
ΔABD≌ΔACD B、ΔABE≌ΔACE C、ΔBED≌ΔCED D、以上答案都不对
3、如图,已知AB=CD,AD=BC, 则( )≌( )
4、如图,AB=CD,BF=DE。AF=CE。那么△ABF与△CDE全等吗?并说明理由。
?5、如图,AB=DC,BF=CE,AF=DE,你能找到一对全等的三角形吗?说明你的理由
6、如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF你能找到哪两个三角形全等?说明你的理由.
7、如图,AD=CB,AB=CD 求证:∠B=∠D
E
D
A
B
C
能力提升
2. 已知:如图AB=CD,AD=BC,E,F是BD上两点,且AE=CF,DE=BF,那么图中共有几对全等的三角形?说明理由.
A
B
C
D
E
F
分析:可先通过观察,初步判断有哪几对三角形全等,然后再根据条件判断。
解: 图中共有3对全等的三角形.
3. 已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
能力提升
A
B
C
D
分析:要说明∠A与∠C相等,可设法使它们在两个可以全等的三角形中,那么,全等三角形的对应角相等,为此变四边形为两个三角形。
解: ∠A=∠C.
连接BD.
因为AB=CD,AD=CB,BD=DB
所以ΔABD≌ΔCDB
所以∠A=∠C.
布置作业:
1、课本99页1、2、3
2、伴你学
谢谢大家
北师大七年级数学下册
第四章 三角形
3 探索三角形全等的条件(第1课时)
教学目标
1、经历探索三角形全等条件的过程,体会利用
操作、归纳得出数学结论的过程;在探索三角
形全等条件及应用的过程中,能够进行有条理
的思考,并能进行简单的推理。
2、掌握三角形全等的 “边边边”(“SSS”)条
件,并能利用这些条件判别两个三角形是否全
等。
3、了解三角形的稳定性及其在生活中的应用。
知识链接
1、全等三角形的__________相等,__________相等.
2、如图1,已知△AOC≌△BOD,则∠A=∠B,∠C=_______,______=∠2,对应边有AC=________,______=OB,______=OD.
3、如图2,已知△AOC≌△DOB,则∠A=∠D,∠C=_______,______=∠2,对应边有AC=_______,OC=_______,AO=_______.
4、判定两个三角形全等,依定义必须满足( )
(A)三边对应相等 (B)三角对应相等
(C)三边对应相等和三角对应相等 (D)不能确定
对应边
对应角
∠ D
∠1
BD
OA
OC
∠B
∠1
DB
OB
DO
C
新知探究
提出问题:我们知道能够完全重合的两个三角形叫做全等三角形。那么判断两个三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?…….
动手操作问题一:
1. 只给一个条件画三角形,这个条件可以是_________,画一画,大家画出的三角形一定全等吗?
一条边或一个角
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
给出两个条件画三角形,有几种可能的情况?画一画,大家画出的三角形全等吗?
1、一边和一角
2、两个角
3、两条边
动手操作问题二:
分别按照下面的条件做一做。
两个条件
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个角为30°,一条边为3cm;
不一定全等
两个条件
30o
3cm
30o
3cm
(2)三角形的两个角分别是:30°,50°;
不一定全等
50o
两个条件
50o
30o
30o
(3)三角形的两条边分别是:4cm,6cm.
不一定全等
6cm
4cm
也不能保证三角形全等.
两个条件
4cm
6cm
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
动手操作问题一二总结:
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
不一定全等
动手操作问题三:
只给一个条件,或只给两个条件,都不能保证画出的三角形一定全等,那么如果给出三个条件画三角形呢?你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
三个条件
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角分别相等的两个三角形不一定全等
三个条件
(2) 给出长度分别为4cm,5cm和7cm的木棒,你能摆出这个三角形吗?把你摆的三角形与同伴摆出的进行比较,它们一定全等吗?
三边分别相等的两个三角形全等
三角形全等判定方法1.
三边分别相等的两个三角形全等。 简写成“边边边”或“SSS”
AB=DE
AC= DF
BC= EF
(SSS)
D
E
F
A
B
C
在△ABC和△DEF中
ABC ≌ DEF
所以
用符号语言表达为:
如右图在四边形ACBD中,AC=AD,BD=BC,则∠C=∠D,请说明理由
例1
A
B
C
D
解:在△ABC与△ABD中
AB= ( )
∵ AC= ( )
=BD ( )
∴△ABC≌ △ABD ( )
∴∠C=∠D ( )
公共边
已知
已知
全等三角形的对应角相等
SSS
AB
AD
BC
变式:已知:如图,AC=AD,BD=BC
求证:AB平分∠ DAC
A
D
B
C
动手操作四:
准备几根硬纸条
(1)取出三根木棒钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根木棒钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?
(3)上面的现象说明了什么?
用三根木棒钉成的一个三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。用四根木棒钉成的框架它的形状是可以改变的,因此,四边形具有不稳定性。
思考:你有办法使四边形的框架的形状不发生变化吗?
图片欣赏
你能说出为什么这些地方是三角形吗?
说说看你有什么收获?
1. 三角形全等的条件:
2. 三角形具有稳定性。
达标测评
1. 两个锐角对应相等的两个直角三角形全等吗?为什么?
不一定全等
解:
A
B
C
D
E
F
RtΔABC和RtΔDEF不全等
2、如图,ΔABC中,AB=AC,BE=EC,则由“SSS”可判定…………………………( )
ΔABD≌ΔACD B、ΔABE≌ΔACE C、ΔBED≌ΔCED D、以上答案都不对
3、如图,已知AB=CD,AD=BC, 则( )≌( )
4、如图,AB=CD,BF=DE。AF=CE。那么△ABF与△CDE全等吗?并说明理由。
?5、如图,AB=DC,BF=CE,AF=DE,你能找到一对全等的三角形吗?说明你的理由
6、如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF你能找到哪两个三角形全等?说明你的理由.
7、如图,AD=CB,AB=CD 求证:∠B=∠D
E
D
A
B
C
能力提升
2. 已知:如图AB=CD,AD=BC,E,F是BD上两点,且AE=CF,DE=BF,那么图中共有几对全等的三角形?说明理由.
A
B
C
D
E
F
分析:可先通过观察,初步判断有哪几对三角形全等,然后再根据条件判断。
解: 图中共有3对全等的三角形.
3. 已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
能力提升
A
B
C
D
分析:要说明∠A与∠C相等,可设法使它们在两个可以全等的三角形中,那么,全等三角形的对应角相等,为此变四边形为两个三角形。
解: ∠A=∠C.
连接BD.
因为AB=CD,AD=CB,BD=DB
所以ΔABD≌ΔCDB
所以∠A=∠C.
布置作业:
1、课本99页1、2、3
2、伴你学
谢谢大家
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
