人教版九年级数学下册第28章:锐角三角函数全章复习 课件(共34张ppt)
文档属性
| 名称 | 人教版九年级数学下册第28章:锐角三角函数全章复习 课件(共34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
小结与复习
第二十八章锐角三角函数
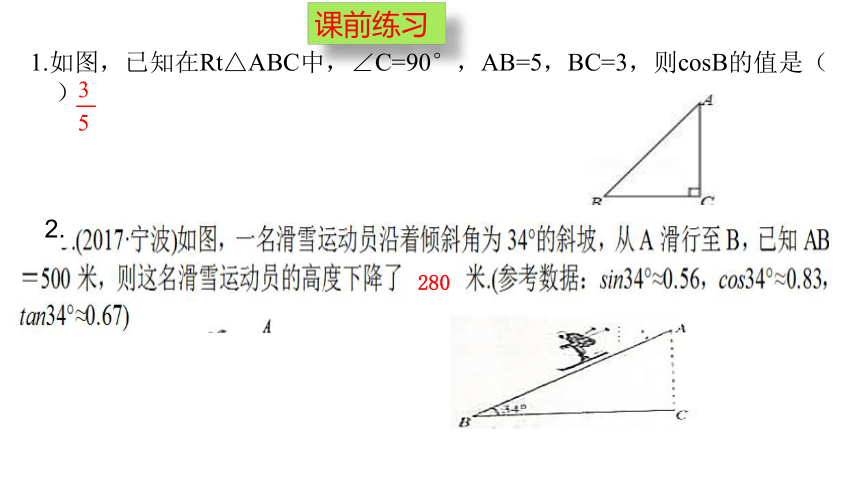
课前练习
1.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
280
2.
3、 Rt△ABC中,∠C=90°,若sinA= ,则cosB的值为( )
17
E
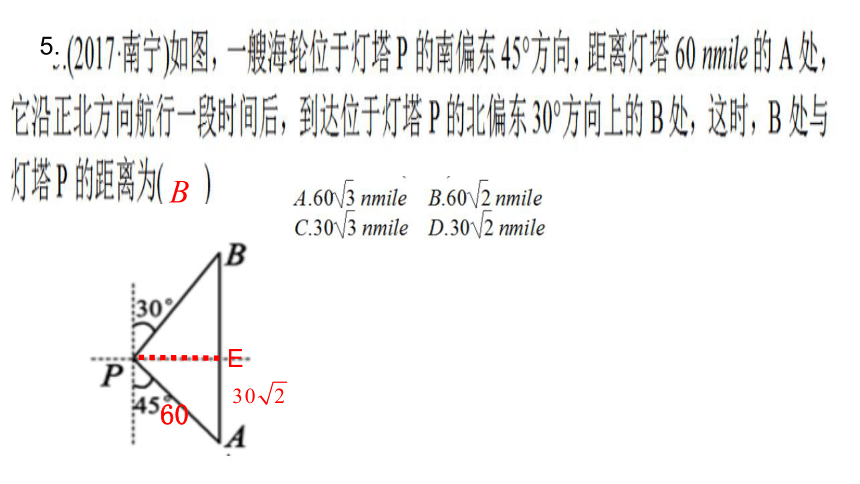
5.
60
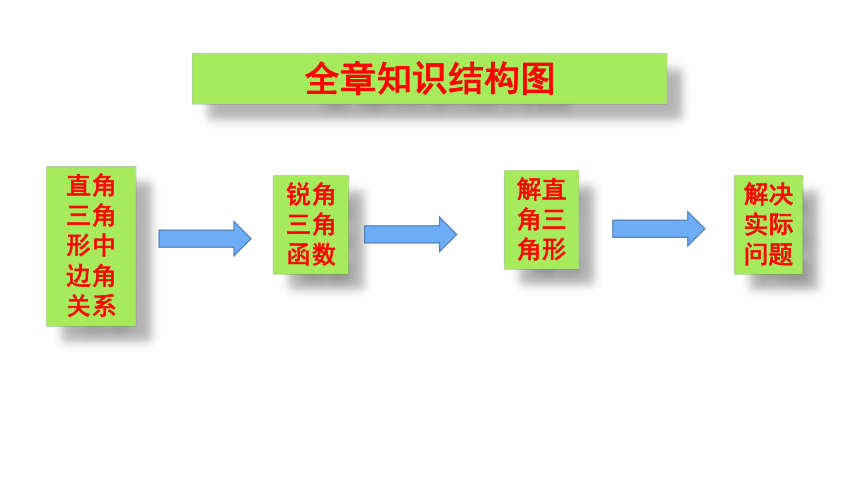
直角三角形中边角关系
锐角三角函数
解直角三角形
解决实际问题
全章知识结构图
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
1. 锐角三角函数定义
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
要点梳理
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
2. 特殊角的三角函数
1
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B,∠C的对边.常用对应关系
三边关系:_______________;
三角关系:_________________ ;
边角关系:sinA=cosB=_____ ,cosA=sinB =____,
tanA=_________,tanB=_______.
a2+b2=c2
∠A=90°-∠B
3. 解直角三角形
?条件:解直角三角形时知道其中的2个元素(至少 有一个是边),就可以求出其余的3个未知元素.
?解法:
①一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题,可通过添加适当的辅助线转化为解直角三角形问题.
(2) 直角三角形可解的条件和解法
(3) 互余两角的三角函数间的关系
sinα = cosα= ,
sin2α + cos2α = .
tanα · tan(90°-α) =___.
cos(90°-α)
sin(90°-α)
1
1
(4) 锐角三角函数的增减性
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
大
小
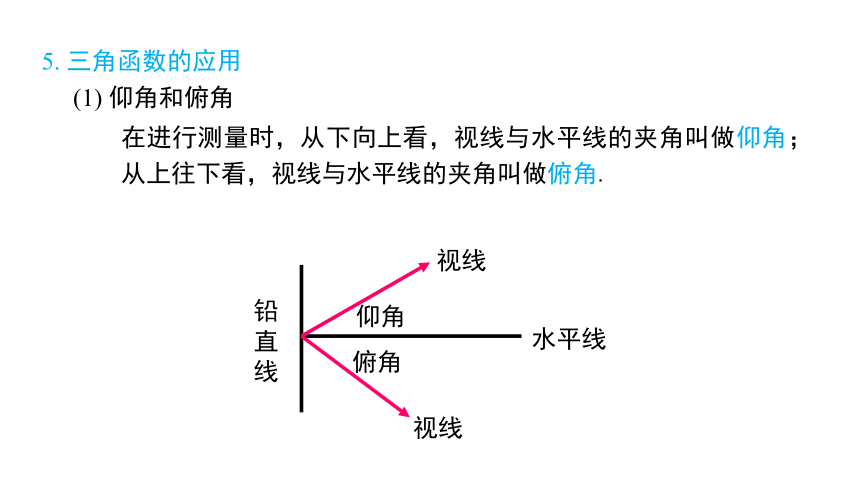
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
5. 三角函数的应用
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡面与水平面的夹角叫做坡角,记作α,有
i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
6. 利用三角函数测高
① 将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
② 根据已知条件中各量之间的关系,适当选用锐角三角函数等去解直角三角形;
③ 如果不是直角三角形,可通过添加辅助线构造直角三角形来解决;
④得到数学问题的答案;进而得到实际问题的答案.
利用解直角三角形的知识解决实际问题的一般过程是:
例1 矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
分析:根据题意,结合折叠的性质,易得∠AFE=∠BCF,进而在Rt△BFC中,有BC=8,CF=10,由勾股定理易得BF的长,根据三角函数的定义,易得 tan∠BCF
的值,借助∠AFE=∠BCF,可得tan∠AFE的值.
10
8
例题讲解
∵∠AFE+∠BFC=90°,∠BCF+∠BFC=90°,
∴∠AFE=∠BCF.
在Rt△BFC中,
10
8
10
10
解: ∵四边形ABCD是矩形,
∴ ∠ D= ∠ A= ∠ B= 90° ,CD=AB=10
由折叠的性质可得, △EDC ≌ △EFC
∴ CF=CD=10,∠EFC=∠EDC=90°.
1 . 在△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
解析:根据sinA= ,可设三角形的两边长分别为4k,5k,则第三边长为3k,所以tanB=
B
针对训练
2. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB, 那么△ABC一定是______三角形.
直角
3. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是____.
针对训练
解:∵在直角△ABD中,
∴BD = AD·tan∠BAD=12× =9,
∴CD=BC-BD=14-9=5,
∴
∴sinC =
4.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,
AD=12,tan∠BAD= ,求sinC的值.
(1)根据特殊角的三角函数值求值;
(2)直接运用三角函数的定义求值;
(3)借助边的数量关系求值;
(4)借助等角求值;
(5)根据三角函数关系求值;
(6)构造直角三角形求值.
方法总结
例2 计算:
解:原式=
针对训练 特殊角的三角函数值
(1) tan30°+cos45°+tan60°;
(2) tan30°· tan60°+ cos230°.
计算:
解:原式
解:原式
针对训练
特殊角与三角函数值的互相转化
3.若0°<∠A<90°,且4sin2A-2=0,则∠A的值是
A.30° B.45° C.60° D.75°
B
4、 如果sin2α+sin230o =1,那么锐角
α的值是( )
15o B. 30o C. 45o D. 60o
D
5、若关于x的一元二次方程:
有两个相等的实数根,求θ的值。
如图所示,在Rt△ABC中,∠C=90°,AC= . 点D为BC边上一点,且BD=2AD,∠ADC=60°.求△ABC的周长 (结果保留根号).
针对训练
解:在Rt△ADC中,
∴BD=2AD=4.
∴BC=BD+DC=5.
在Rt△ABC中,
∴△ABC的周长为AB+BC+AC
针对训练 解直角三角形
第19题图
(2019?襄阳)襄阳卧龙大桥横跨汉江,是我市标志性建筑之一.某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发没AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°.请求出塔冠BE的高度(结果精确到0.1m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
则BC=AC?tanA≈121×0.75=90.75,
由题意得,
CD=AC﹣AD=121-23.5=97.5,
在Rt△ECD中,∠EDC=45°,
∴EC=CD=97.5,
∴BE=EC﹣BC
=97.5-90.75=6.75≈6.8(m)
答:塔冠BE的高度约为6.8m.
考点四 三角函数的应用
E
F
53
1.
针对训练 解直角三角形应用
2.如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是 km.
针对训练 解直角三角形应用
3. 某海滨浴场东西走向的海岸线可近似看作直线l (如图). 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是 2 米/秒,则谁先到达 B 处?请说明理由 (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43).
分析: 在Rt△CDB中,利用三角函数即可求得BC,BD的长,则可求得甲、乙所用的时间,比较二者之间的大小即可.
针对训练 解直角三角形应用
解:由题意得∠BCD=55°,∠BDC=90°.
∴BD=CD · tan∠BCD=40×tan55°≈57.2(米).
BC= = ≈70.2(米).
∴t甲≈57.22÷2+10=38.6(秒),
t乙≈70.22÷2=35.1(秒).
∴t甲>t乙.
答:乙先到达B处.
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
课堂小结
正弦
锐
角
三
角
函
数
余弦
正切
三边关系
三角关系
边角关系
仰俯角问题
方位角问题
坡度问题
作业布置
小结与复习
第二十八章锐角三角函数
课前练习
1.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
280
2.
3、 Rt△ABC中,∠C=90°,若sinA= ,则cosB的值为( )
17
E
5.
60
直角三角形中边角关系
锐角三角函数
解直角三角形
解决实际问题
全章知识结构图
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
1. 锐角三角函数定义
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
要点梳理
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
2. 特殊角的三角函数
1
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B,∠C的对边.常用对应关系
三边关系:_______________;
三角关系:_________________ ;
边角关系:sinA=cosB=_____ ,cosA=sinB =____,
tanA=_________,tanB=_______.
a2+b2=c2
∠A=90°-∠B
3. 解直角三角形
?条件:解直角三角形时知道其中的2个元素(至少 有一个是边),就可以求出其余的3个未知元素.
?解法:
①一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题,可通过添加适当的辅助线转化为解直角三角形问题.
(2) 直角三角形可解的条件和解法
(3) 互余两角的三角函数间的关系
sinα = cosα= ,
sin2α + cos2α = .
tanα · tan(90°-α) =___.
cos(90°-α)
sin(90°-α)
1
1
(4) 锐角三角函数的增减性
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
大
小
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
5. 三角函数的应用
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡面与水平面的夹角叫做坡角,记作α,有
i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
6. 利用三角函数测高
① 将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
② 根据已知条件中各量之间的关系,适当选用锐角三角函数等去解直角三角形;
③ 如果不是直角三角形,可通过添加辅助线构造直角三角形来解决;
④得到数学问题的答案;进而得到实际问题的答案.
利用解直角三角形的知识解决实际问题的一般过程是:
例1 矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
分析:根据题意,结合折叠的性质,易得∠AFE=∠BCF,进而在Rt△BFC中,有BC=8,CF=10,由勾股定理易得BF的长,根据三角函数的定义,易得 tan∠BCF
的值,借助∠AFE=∠BCF,可得tan∠AFE的值.
10
8
例题讲解
∵∠AFE+∠BFC=90°,∠BCF+∠BFC=90°,
∴∠AFE=∠BCF.
在Rt△BFC中,
10
8
10
10
解: ∵四边形ABCD是矩形,
∴ ∠ D= ∠ A= ∠ B= 90° ,CD=AB=10
由折叠的性质可得, △EDC ≌ △EFC
∴ CF=CD=10,∠EFC=∠EDC=90°.
1 . 在△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
解析:根据sinA= ,可设三角形的两边长分别为4k,5k,则第三边长为3k,所以tanB=
B
针对训练
2. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB, 那么△ABC一定是______三角形.
直角
3. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是____.
针对训练
解:∵在直角△ABD中,
∴BD = AD·tan∠BAD=12× =9,
∴CD=BC-BD=14-9=5,
∴
∴sinC =
4.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,
AD=12,tan∠BAD= ,求sinC的值.
(1)根据特殊角的三角函数值求值;
(2)直接运用三角函数的定义求值;
(3)借助边的数量关系求值;
(4)借助等角求值;
(5)根据三角函数关系求值;
(6)构造直角三角形求值.
方法总结
例2 计算:
解:原式=
针对训练 特殊角的三角函数值
(1) tan30°+cos45°+tan60°;
(2) tan30°· tan60°+ cos230°.
计算:
解:原式
解:原式
针对训练
特殊角与三角函数值的互相转化
3.若0°<∠A<90°,且4sin2A-2=0,则∠A的值是
A.30° B.45° C.60° D.75°
B
4、 如果sin2α+sin230o =1,那么锐角
α的值是( )
15o B. 30o C. 45o D. 60o
D
5、若关于x的一元二次方程:
有两个相等的实数根,求θ的值。
如图所示,在Rt△ABC中,∠C=90°,AC= . 点D为BC边上一点,且BD=2AD,∠ADC=60°.求△ABC的周长 (结果保留根号).
针对训练
解:在Rt△ADC中,
∴BD=2AD=4.
∴BC=BD+DC=5.
在Rt△ABC中,
∴△ABC的周长为AB+BC+AC
针对训练 解直角三角形
第19题图
(2019?襄阳)襄阳卧龙大桥横跨汉江,是我市标志性建筑之一.某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发没AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°.请求出塔冠BE的高度(结果精确到0.1m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
则BC=AC?tanA≈121×0.75=90.75,
由题意得,
CD=AC﹣AD=121-23.5=97.5,
在Rt△ECD中,∠EDC=45°,
∴EC=CD=97.5,
∴BE=EC﹣BC
=97.5-90.75=6.75≈6.8(m)
答:塔冠BE的高度约为6.8m.
考点四 三角函数的应用
E
F
53
1.
针对训练 解直角三角形应用
2.如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是 km.
针对训练 解直角三角形应用
3. 某海滨浴场东西走向的海岸线可近似看作直线l (如图). 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是 2 米/秒,则谁先到达 B 处?请说明理由 (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43).
分析: 在Rt△CDB中,利用三角函数即可求得BC,BD的长,则可求得甲、乙所用的时间,比较二者之间的大小即可.
针对训练 解直角三角形应用
解:由题意得∠BCD=55°,∠BDC=90°.
∴BD=CD · tan∠BCD=40×tan55°≈57.2(米).
BC= = ≈70.2(米).
∴t甲≈57.22÷2+10=38.6(秒),
t乙≈70.22÷2=35.1(秒).
∴t甲>t乙.
答:乙先到达B处.
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
课堂小结
正弦
锐
角
三
角
函
数
余弦
正切
三边关系
三角关系
边角关系
仰俯角问题
方位角问题
坡度问题
作业布置
