北师大版七年级数学下册 2.1 两条直线的位置关系课件(第1课时 共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.1 两条直线的位置关系课件(第1课时 共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 20:23:41 | ||
图片预览





文档简介
(共23张PPT)
一
学科:数学
年级:七年级
版本:北师大2011课标版 下册
课程名称:对顶角、余角、补角
两条直线的位置关系
——对顶角、余角和补角
第二章 相交线与平行线
一
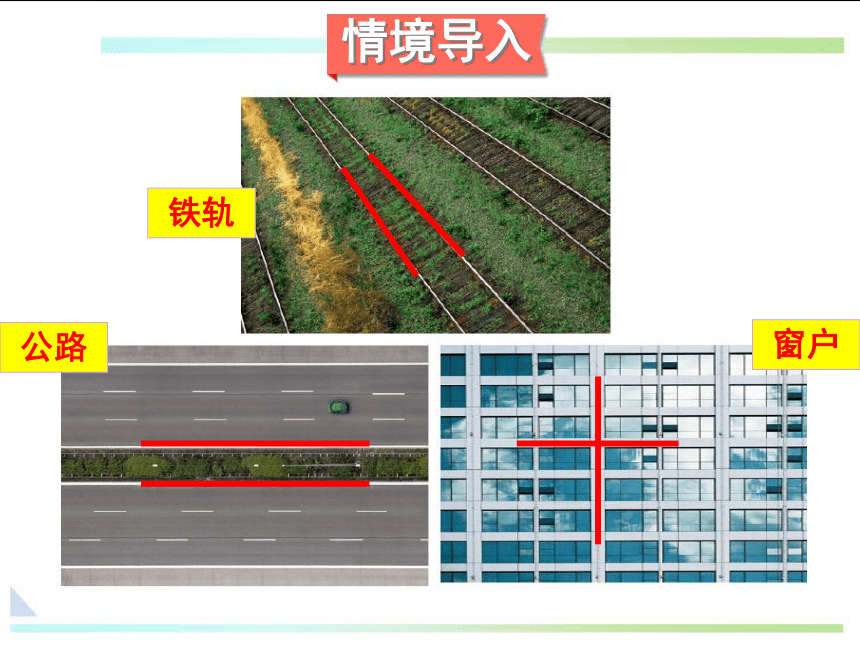
铁轨
公路
窗户
情境导入
学习目标
一
1.了解平面内两条直线的位置关系.
2.在具体情境中理解对顶角、余角、补角的概念.
3.通过观察、操作、推理、交流等过程,掌握对顶角、余角、补角的性质.
阅读课本38、39页,独立完成以下问题,2分钟
1. ,我们称这两条直线为相交线.
2. , 的两条直线叫做平行线.
4.如果两个角的和是 ,那么称这两个角互为补角.
5.如果两个角的和是90°,那么称这两个角互为 .
若两条直线只有一个公共点
不相交
在同一个平面内
预习检测
一
180°
余角
2
一
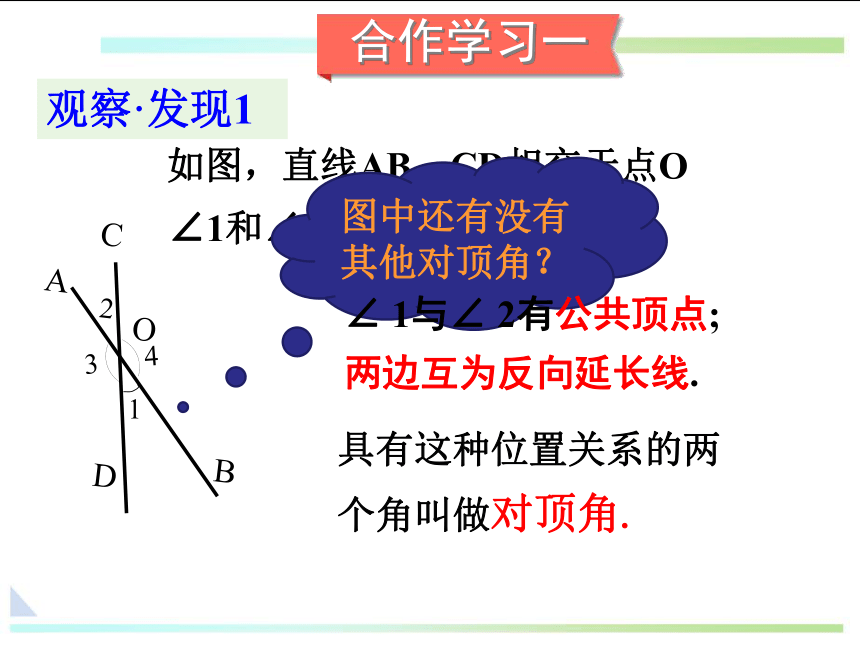
如图,直线AB、CD相交于点O
1
A
B
C
D
O
3
4
∠1和∠2的位置有什么关系?
图中还有没有其他对顶角?
观察·发现1
合作学习一
∠ 1与∠ 2有公共顶点;
两边互为反向延长线.
具有这种位置关系的两个角叫做对顶角.
一
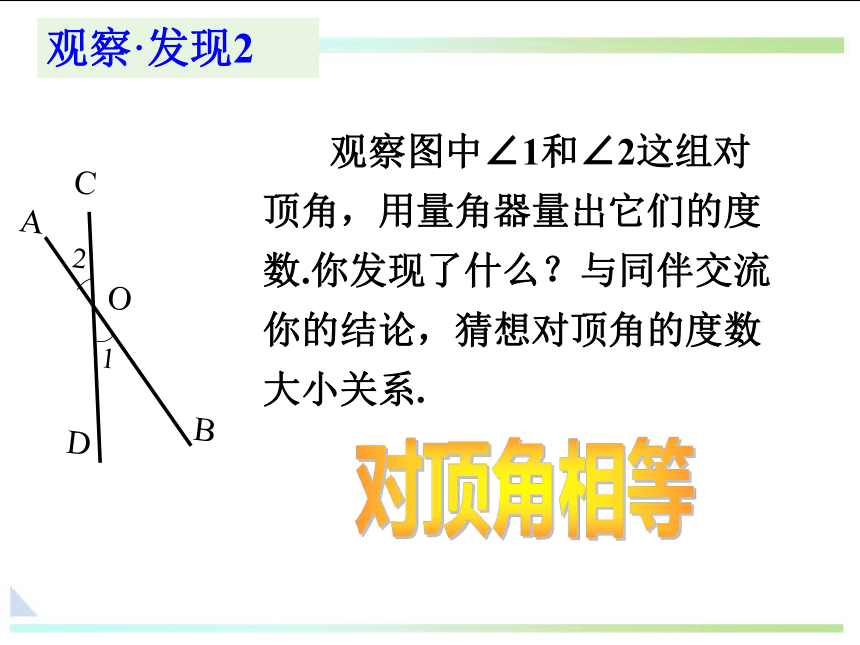
观察图中∠1和∠2这组对顶角,用量角器量出它们的度数.你发现了什么?与同伴交流你的结论,猜想对顶角的度数大小关系.
观察·发现2
2
1
A
B
C
D
O
对顶角相等
一
归纳总结一
1、两角有公共顶点,并且它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
2、对顶角相等.
一
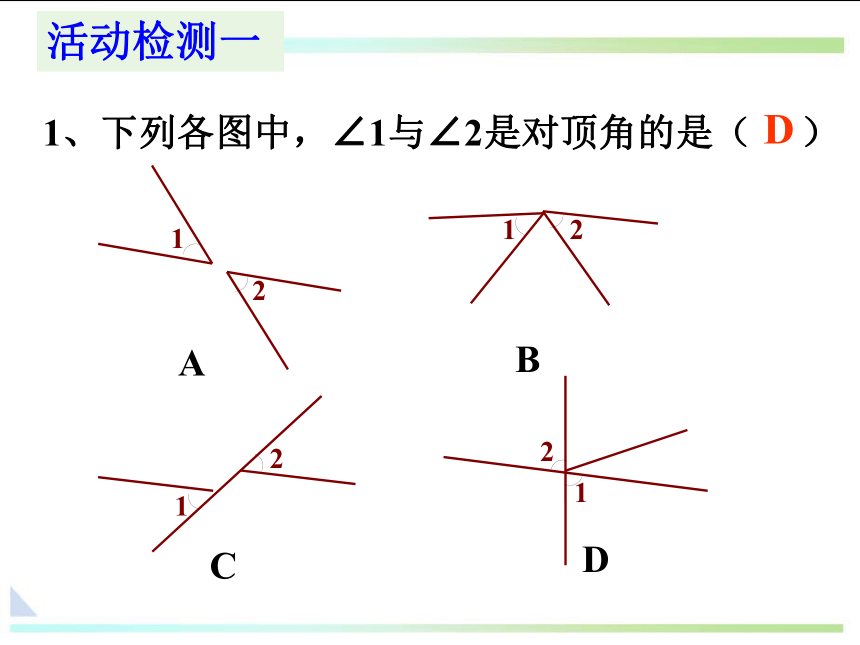
活动检测一
1、下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
一
活动检测一
2、如图所示,直线AB、CD相交于点O,OE是射线, ∠AOE=90°,则∠1的对顶角是 ,∠4的对顶角是 .
∠BOC
∠3
O
2
1
3
4
E
A
B
D
C
一
(2)互补、互余的两角一定有公共顶点或公共边吗?
(1)∠1 + ∠2 + ∠3 = 180°,能说∠1 、∠2、 ∠3 互补吗?
1、定义:
如果两个角的和是90?,那么称两个角互为
如果两个角的和是180?,那么称两个角互为
2、问题:
合作学习二
补角.
余角.
一
∠α ∠α的余角 ∠α的补角
5°
77°
62°23′
85°
13°
27°37′
175°
103°
117°37′
活动检测二
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
1、哪些角互为补角?哪些角互为余角?
2、∠3与∠4有什么关系?为什么?
3、∠AOC与∠BOD有什么关系?为什么?
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
1、哪些角互为补角?哪些角互为余角?
互补:∠1和∠AOC,∠2和∠BON,
∠DON与∠CON
互余:∠1与∠3, ∠2与∠4
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
2、∠3与∠4有什么关系?为什么?
因为 ∠3=90°- ∠1, ∠4=90°- ∠ 2
而 ∠1= ∠2
所以 ∠3= ∠4
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
3、∠AOC与∠BOD有什么关系?为什么?
因为∠AOC=180°- ∠1, ∠BOD=180°- ∠ 2
而 ∠1= ∠2
所以∠AOC= ∠BOD
一
归纳总结二
同角或等角的补角相等
同角或等角的余角相等
一
1.已知∠A=100°,那么∠A补角为 度.
2.(2016广西)下列各图中,∠1与∠2互为余角的是( )
活动检测三
80
1
2
1
2
2
2
1
1
A.
B.
C.
D.
C
课堂小结
一
1.相交线和平行线
2.对顶角
性质:对顶角相等
3.补角
性质:同角或等角的补角相等
4.余角
性质:同角或等角的余角相等
一
达标检测
2. (2016吉林)如图是对顶角量角器,用它测量角的原理是 .
对顶角相等
1.在同一平面内,两条直线的位置关系有
和 .
相交
平行
3.(2017湖南)已知∠1=24°,且∠1与∠2互余,∠2与∠3互余,则∠3的余角和补角的度数分别为 .
66°和156°
一
达标检测
4.(2017山东)如果一个角的补角是120°,那么这个角的余角是( )
A. 150° B. 90° C. 60° D. 30°
5.一副三角尺按如图的方式摆放,且∠1比∠2大54°,则∠1的度数是( )
A. 18° B. 54° C. 72° D. 70°
解:设∠1的度数为 x ,可得
x – ( 90° – x) = 54°
解得 x =72°
D
C
习题2.1 第1,2,3题
课后作业
一
一
下课啦!
一
学科:数学
年级:七年级
版本:北师大2011课标版 下册
课程名称:对顶角、余角、补角
两条直线的位置关系
——对顶角、余角和补角
第二章 相交线与平行线
一
铁轨
公路
窗户
情境导入
学习目标
一
1.了解平面内两条直线的位置关系.
2.在具体情境中理解对顶角、余角、补角的概念.
3.通过观察、操作、推理、交流等过程,掌握对顶角、余角、补角的性质.
阅读课本38、39页,独立完成以下问题,2分钟
1. ,我们称这两条直线为相交线.
2. , 的两条直线叫做平行线.
4.如果两个角的和是 ,那么称这两个角互为补角.
5.如果两个角的和是90°,那么称这两个角互为 .
若两条直线只有一个公共点
不相交
在同一个平面内
预习检测
一
180°
余角
2
一
如图,直线AB、CD相交于点O
1
A
B
C
D
O
3
4
∠1和∠2的位置有什么关系?
图中还有没有其他对顶角?
观察·发现1
合作学习一
∠ 1与∠ 2有公共顶点;
两边互为反向延长线.
具有这种位置关系的两个角叫做对顶角.
一
观察图中∠1和∠2这组对顶角,用量角器量出它们的度数.你发现了什么?与同伴交流你的结论,猜想对顶角的度数大小关系.
观察·发现2
2
1
A
B
C
D
O
对顶角相等
一
归纳总结一
1、两角有公共顶点,并且它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
2、对顶角相等.
一
活动检测一
1、下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
一
活动检测一
2、如图所示,直线AB、CD相交于点O,OE是射线, ∠AOE=90°,则∠1的对顶角是 ,∠4的对顶角是 .
∠BOC
∠3
O
2
1
3
4
E
A
B
D
C
一
(2)互补、互余的两角一定有公共顶点或公共边吗?
(1)∠1 + ∠2 + ∠3 = 180°,能说∠1 、∠2、 ∠3 互补吗?
1、定义:
如果两个角的和是90?,那么称两个角互为
如果两个角的和是180?,那么称两个角互为
2、问题:
合作学习二
补角.
余角.
一
∠α ∠α的余角 ∠α的补角
5°
77°
62°23′
85°
13°
27°37′
175°
103°
117°37′
活动检测二
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
1、哪些角互为补角?哪些角互为余角?
2、∠3与∠4有什么关系?为什么?
3、∠AOC与∠BOD有什么关系?为什么?
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
1、哪些角互为补角?哪些角互为余角?
互补:∠1和∠AOC,∠2和∠BON,
∠DON与∠CON
互余:∠1与∠3, ∠2与∠4
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
2、∠3与∠4有什么关系?为什么?
因为 ∠3=90°- ∠1, ∠4=90°- ∠ 2
而 ∠1= ∠2
所以 ∠3= ∠4
一
N
2
D
C
O
1
3
4
A
B
∠DON=∠CON=900,∠1=∠2。
合作学习三
3、∠AOC与∠BOD有什么关系?为什么?
因为∠AOC=180°- ∠1, ∠BOD=180°- ∠ 2
而 ∠1= ∠2
所以∠AOC= ∠BOD
一
归纳总结二
同角或等角的补角相等
同角或等角的余角相等
一
1.已知∠A=100°,那么∠A补角为 度.
2.(2016广西)下列各图中,∠1与∠2互为余角的是( )
活动检测三
80
1
2
1
2
2
2
1
1
A.
B.
C.
D.
C
课堂小结
一
1.相交线和平行线
2.对顶角
性质:对顶角相等
3.补角
性质:同角或等角的补角相等
4.余角
性质:同角或等角的余角相等
一
达标检测
2. (2016吉林)如图是对顶角量角器,用它测量角的原理是 .
对顶角相等
1.在同一平面内,两条直线的位置关系有
和 .
相交
平行
3.(2017湖南)已知∠1=24°,且∠1与∠2互余,∠2与∠3互余,则∠3的余角和补角的度数分别为 .
66°和156°
一
达标检测
4.(2017山东)如果一个角的补角是120°,那么这个角的余角是( )
A. 150° B. 90° C. 60° D. 30°
5.一副三角尺按如图的方式摆放,且∠1比∠2大54°,则∠1的度数是( )
A. 18° B. 54° C. 72° D. 70°
解:设∠1的度数为 x ,可得
x – ( 90° – x) = 54°
解得 x =72°
D
C
习题2.1 第1,2,3题
课后作业
一
一
下课啦!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
