高二物理选修3-4 11.简谐运动复习课件(27张ppt人教版)
文档属性
| 名称 | 高二物理选修3-4 11.简谐运动复习课件(27张ppt人教版) |  | |
| 格式 | zip | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-27 20:37:57 | ||
图片预览




文档简介
(共36张PPT)
简谐运动
1、弹簧振子
2、单摆
理想化模型
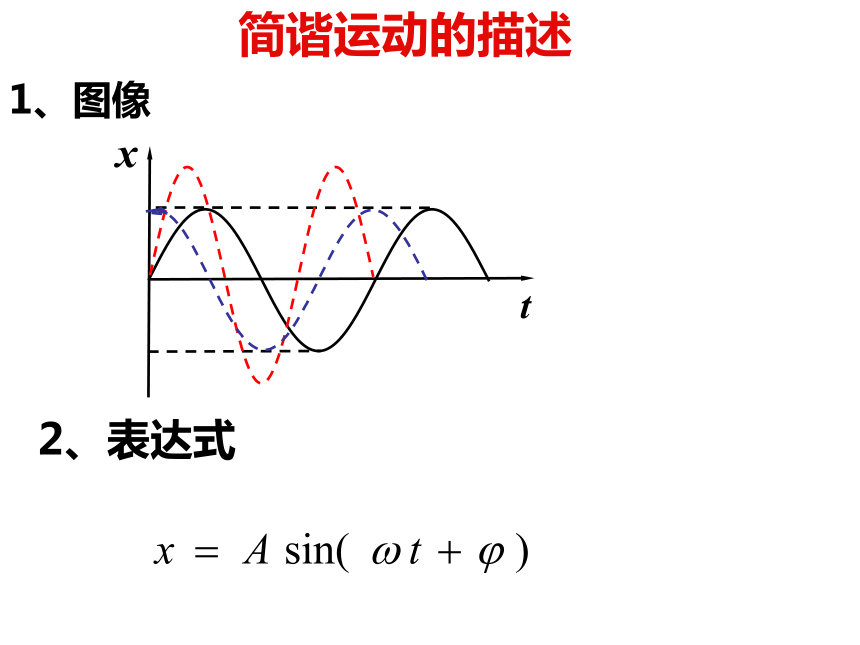
简谐运动的描述
1、图像
2、表达式
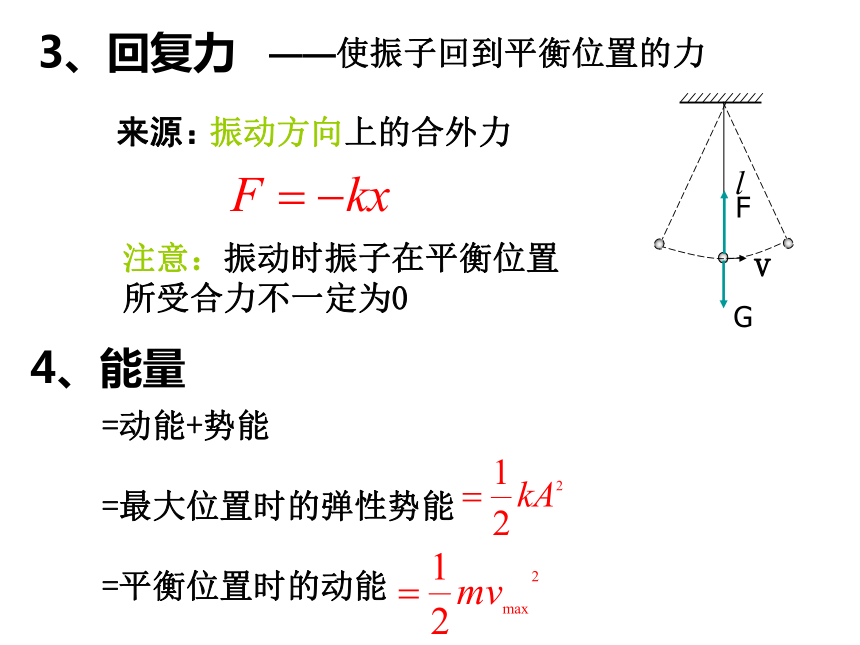
3、回复力
=动能+势能
=最大位置时的弹性势能
=平衡位置时的动能
4、能量
——使振子回到平衡位置的力
来源:
振动方向上的合外力
注意:振动时振子在平衡位置所受合力不一定为0
1、做简谐运动的弹簧振子,在某段时间内速度越来越大,则在这段时间内( )
A、振子的位移越来越大
B、振子正向平衡位置运动
C、振子的速度与位移同向
D、振子的速度与位移反向
BD
练习:
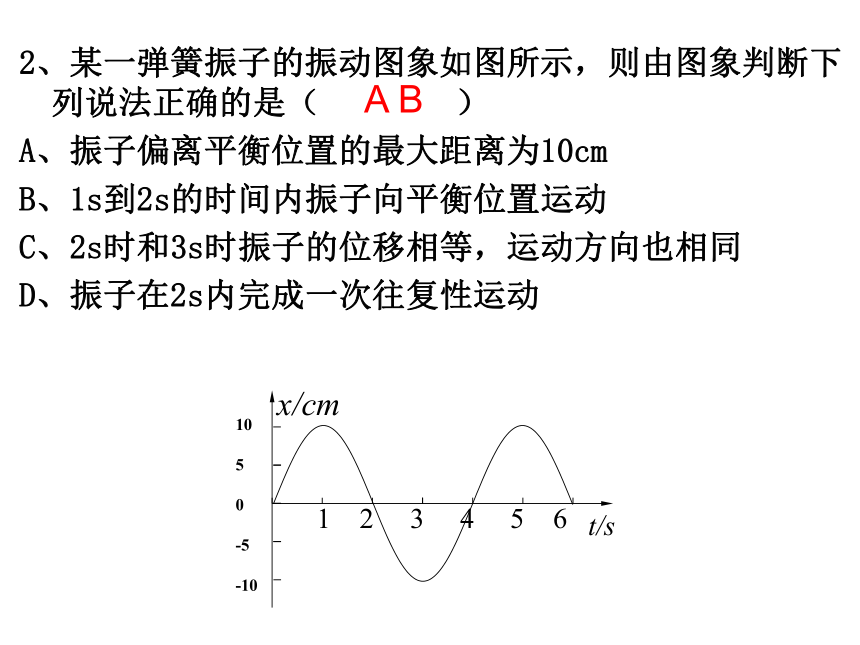
2、某一弹簧振子的振动图象如图所示,则由图象判断下列说法正确的是( )
A、振子偏离平衡位置的最大距离为10cm
B、1s到2s的时间内振子向平衡位置运动
C、2s时和3s时振子的位移相等,运动方向也相同
D、振子在2s内完成一次往复性运动
A B
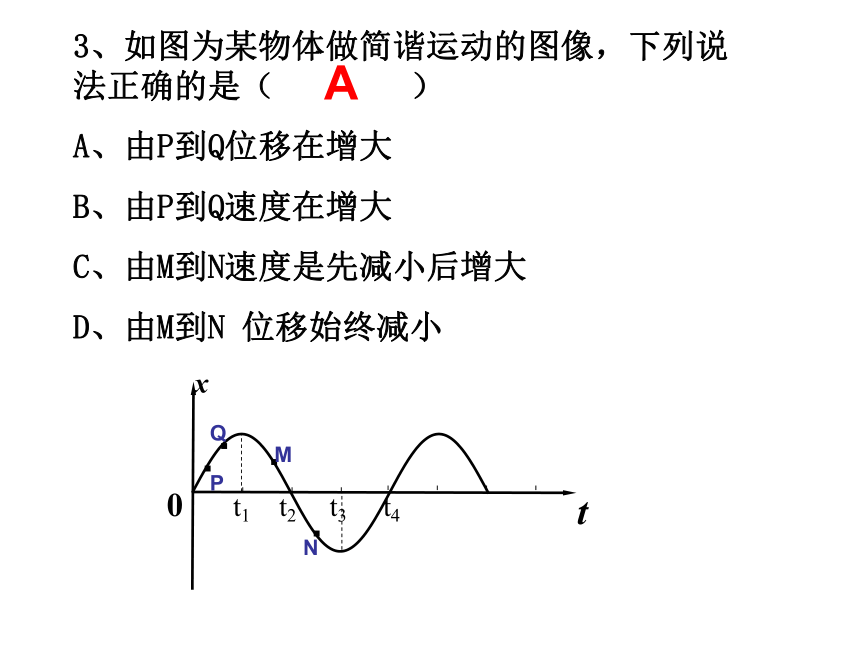
3、如图为某物体做简谐运动的图像,下列说法正确的是( )
A、由P到Q位移在增大
B、由P到Q速度在增大
C、由M到N速度是先减小后增大
D、由M到N 位移始终减小
A
4、一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13s质点第一次通过M点,再经0.1s第二次通过M点,则质点振动周期的可能值为多大?
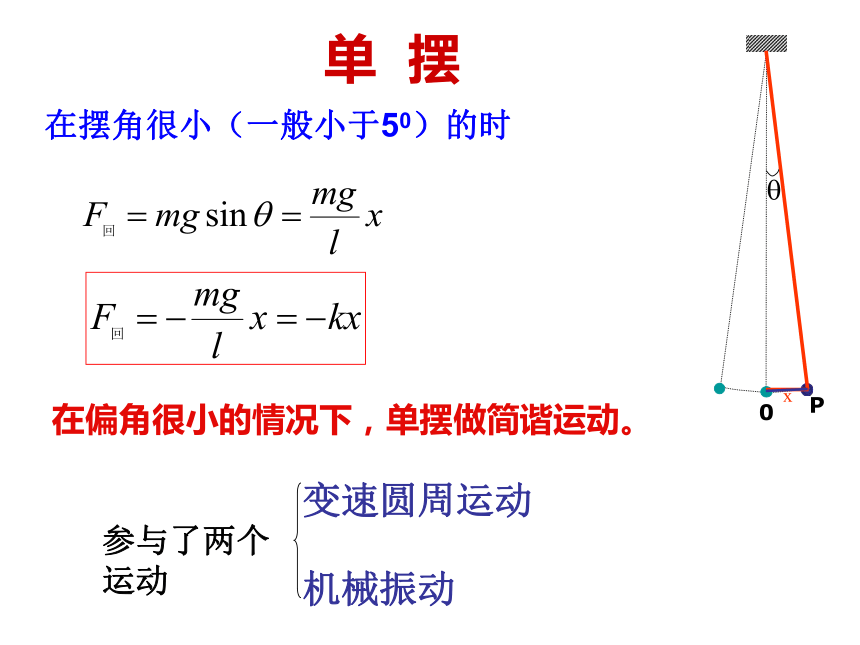
在摆角很小(一般小于50)的时
在偏角很小的情况下,单摆做简谐运动。
单 摆
变速圆周运动
机械振动
参与了两个运动
2.单摆作简谐运动时的回复力是:
A.摆球的重力 B.摆球重力沿圆弧切线的分力
C.摆线的拉力 D.摆球重力与摆线拉力的合力
B
1、关于单摆的振动,以下说法正确的是( )
A.摆球摆到最高点时,所受合外力为零
B.摆球摆到最高点时,所受合外力指向悬点
C.摆球摆到最低点时,所受合外力指向悬点
D.摆球摆到最低点时,所受合外力为零.
C
练习:
3、振动的单摆小球通过平衡位置时,关于小球受到的回复力及合外力的说法正确的是( )
A.回复力为零,合外力不为零,方向指向悬点
B.回复力不为零,方向沿轨迹的切线
C.合外力不为零,方向沿轨迹的切线
D.回复力为零,合外力也为零
A
单摆的周期
摆长
L=L0+R
例:在下述哪些情况下单摆的简谐振动周期会变大?
A.摆球质量增大
B.摆长减小
C.单摆由赤道移到北京
D.单摆由海平面移到高山顶上
练习1:用空心铁球内部装满水做摆球,若球正下方有一小孔,水不断从孔中流出,从球内装满水到水流完为止的过程中,其振动周期的大小是 [ ]
A.不变
B.变大
C.先变大后变小回到原值
D.先变小后变大回到原值
c
1、如图所示,三根细线在O点处打结,A、B端固定在同一水平面上相距为L的两点上,使AOB成直角三角形,已知OC线长为L,下端C点系着一个小球,让小球在垂直纸面内振动,振动周期为多少?
★确定等效悬点及摆长l’
O’
确定等效的重力加速度g’
确定等效重力加速度的方法:
(1)确定摆球的平衡位置
(2)确定摆球静止在平衡位置时摆线上的拉力T
(3)等效重力加速度g’=T/m
2、如图所示,摆长为l的单摆安置在倾角为α的光滑斜面上,设重力加速度为g,这个单摆的振动周期T等于多少?
例:小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了. 问:(1)这个摆钟到北京后是否还准时? (2)若不准,是偏慢还是偏快? (3)如须调整应该怎样调节?
单摆的应用
1.利用它的等时性计时
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
2、测重力加速度
【实验原理】
【实验器材】
金属球、细线、铁架台、铁夹;
刻度尺、游标卡尺、秒表。
【实验步骤】
1.实际单摆的制作——要注意以下几点:
①.摆的振幅不要太大(即:偏角很小)
②.摆球和摆线的选择
摆线:细、伸缩性小、质量可忽略、尽可能长一些
摆球:质量大、体积小
③.细线上端的悬挂方式
图甲、乙两图画出了细线上端的两种不同的悬挂方式,哪种比较好?为什么?
方法一:平均值法,将测得的几次的周期T和摆长L代入公式:g= 4p2 L/T2 中算出重力加速度g 的值,再算出g的平均值。
方法二:图象法,由单摆的周期公式:
因此以摆长L为纵轴,以T2为横轴,做出L-T2图象,是一条过原点的直线,如图,求出斜率k,即可求出g值。
g=4π2k,k=△L/△T2。
【数据处理】
课 堂 练 习
1:在“用单摆测定重力加速度的实验中”
①用游标卡尺测量摆球直径的情况如下图所示,读出摆球直径_________cm 。
②测单摆周期时,当摆球经过平衡位置时开始计时并计1次,测出经过该位置N次所用时间为t,则单摆周期为______________。
③若测量出多组周期T、摆长L数值后,画出T2—L图象如图,则此图线的斜率的物理意义是__________。
2.06
2t/(N-1)
4p2 / g
2: 某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图所示。
他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=______。
请你判断该同学得到的
实验结果与摆球重心就在球
心处的情况相比,将______。
(填偏大、偏小或相同)
振动系统不受外力作用的振动叫固有振动
振动的频率叫固有频率
振动的周期叫固有周期
1、定义:系统受到了阻力作用,振幅越来越小的振动
一、阻尼振动
2、图像:
问题1:为什么做阻尼振动的物体,振幅要越来越小呢?
由于振动物体要克服阻尼的作用做功,系统的机械能逐渐减小,故振动的振幅也逐渐减小。
问题2:阻尼振动中,在振幅逐渐减小的过程中,振子的周期如何变化?
不变,因为周期与振幅无关
二、受迫振动
1、驱动力:作用在振动物体上的周期性外力
2、受迫振动:物体在外界驱动力作用下的振动
3、受迫振动频率:
振动稳定后的频率等于驱动力的频率,跟物体的固有频率无关
4、受迫振动振幅:
驱动力的频率等于振动物体的固有频率时,振幅最大;驱动力的频率跟固有频率相差越大,振幅越小
f驱= f固时,振幅有最大值
f驱与 f固差别越大时,振幅越小
(共振)
简谐运动
1、弹簧振子
2、单摆
理想化模型
简谐运动的描述
1、图像
2、表达式
3、回复力
=动能+势能
=最大位置时的弹性势能
=平衡位置时的动能
4、能量
——使振子回到平衡位置的力
来源:
振动方向上的合外力
注意:振动时振子在平衡位置所受合力不一定为0
1、做简谐运动的弹簧振子,在某段时间内速度越来越大,则在这段时间内( )
A、振子的位移越来越大
B、振子正向平衡位置运动
C、振子的速度与位移同向
D、振子的速度与位移反向
BD
练习:
2、某一弹簧振子的振动图象如图所示,则由图象判断下列说法正确的是( )
A、振子偏离平衡位置的最大距离为10cm
B、1s到2s的时间内振子向平衡位置运动
C、2s时和3s时振子的位移相等,运动方向也相同
D、振子在2s内完成一次往复性运动
A B
3、如图为某物体做简谐运动的图像,下列说法正确的是( )
A、由P到Q位移在增大
B、由P到Q速度在增大
C、由M到N速度是先减小后增大
D、由M到N 位移始终减小
A
4、一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13s质点第一次通过M点,再经0.1s第二次通过M点,则质点振动周期的可能值为多大?
在摆角很小(一般小于50)的时
在偏角很小的情况下,单摆做简谐运动。
单 摆
变速圆周运动
机械振动
参与了两个运动
2.单摆作简谐运动时的回复力是:
A.摆球的重力 B.摆球重力沿圆弧切线的分力
C.摆线的拉力 D.摆球重力与摆线拉力的合力
B
1、关于单摆的振动,以下说法正确的是( )
A.摆球摆到最高点时,所受合外力为零
B.摆球摆到最高点时,所受合外力指向悬点
C.摆球摆到最低点时,所受合外力指向悬点
D.摆球摆到最低点时,所受合外力为零.
C
练习:
3、振动的单摆小球通过平衡位置时,关于小球受到的回复力及合外力的说法正确的是( )
A.回复力为零,合外力不为零,方向指向悬点
B.回复力不为零,方向沿轨迹的切线
C.合外力不为零,方向沿轨迹的切线
D.回复力为零,合外力也为零
A
单摆的周期
摆长
L=L0+R
例:在下述哪些情况下单摆的简谐振动周期会变大?
A.摆球质量增大
B.摆长减小
C.单摆由赤道移到北京
D.单摆由海平面移到高山顶上
练习1:用空心铁球内部装满水做摆球,若球正下方有一小孔,水不断从孔中流出,从球内装满水到水流完为止的过程中,其振动周期的大小是 [ ]
A.不变
B.变大
C.先变大后变小回到原值
D.先变小后变大回到原值
c
1、如图所示,三根细线在O点处打结,A、B端固定在同一水平面上相距为L的两点上,使AOB成直角三角形,已知OC线长为L,下端C点系着一个小球,让小球在垂直纸面内振动,振动周期为多少?
★确定等效悬点及摆长l’
O’
确定等效的重力加速度g’
确定等效重力加速度的方法:
(1)确定摆球的平衡位置
(2)确定摆球静止在平衡位置时摆线上的拉力T
(3)等效重力加速度g’=T/m
2、如图所示,摆长为l的单摆安置在倾角为α的光滑斜面上,设重力加速度为g,这个单摆的振动周期T等于多少?
例:小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了. 问:(1)这个摆钟到北京后是否还准时? (2)若不准,是偏慢还是偏快? (3)如须调整应该怎样调节?
单摆的应用
1.利用它的等时性计时
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
2、测重力加速度
【实验原理】
【实验器材】
金属球、细线、铁架台、铁夹;
刻度尺、游标卡尺、秒表。
【实验步骤】
1.实际单摆的制作——要注意以下几点:
①.摆的振幅不要太大(即:偏角很小)
②.摆球和摆线的选择
摆线:细、伸缩性小、质量可忽略、尽可能长一些
摆球:质量大、体积小
③.细线上端的悬挂方式
图甲、乙两图画出了细线上端的两种不同的悬挂方式,哪种比较好?为什么?
方法一:平均值法,将测得的几次的周期T和摆长L代入公式:g= 4p2 L/T2 中算出重力加速度g 的值,再算出g的平均值。
方法二:图象法,由单摆的周期公式:
因此以摆长L为纵轴,以T2为横轴,做出L-T2图象,是一条过原点的直线,如图,求出斜率k,即可求出g值。
g=4π2k,k=△L/△T2。
【数据处理】
课 堂 练 习
1:在“用单摆测定重力加速度的实验中”
①用游标卡尺测量摆球直径的情况如下图所示,读出摆球直径_________cm 。
②测单摆周期时,当摆球经过平衡位置时开始计时并计1次,测出经过该位置N次所用时间为t,则单摆周期为______________。
③若测量出多组周期T、摆长L数值后,画出T2—L图象如图,则此图线的斜率的物理意义是__________。
2.06
2t/(N-1)
4p2 / g
2: 某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图所示。
他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=______。
请你判断该同学得到的
实验结果与摆球重心就在球
心处的情况相比,将______。
(填偏大、偏小或相同)
振动系统不受外力作用的振动叫固有振动
振动的频率叫固有频率
振动的周期叫固有周期
1、定义:系统受到了阻力作用,振幅越来越小的振动
一、阻尼振动
2、图像:
问题1:为什么做阻尼振动的物体,振幅要越来越小呢?
由于振动物体要克服阻尼的作用做功,系统的机械能逐渐减小,故振动的振幅也逐渐减小。
问题2:阻尼振动中,在振幅逐渐减小的过程中,振子的周期如何变化?
不变,因为周期与振幅无关
二、受迫振动
1、驱动力:作用在振动物体上的周期性外力
2、受迫振动:物体在外界驱动力作用下的振动
3、受迫振动频率:
振动稳定后的频率等于驱动力的频率,跟物体的固有频率无关
4、受迫振动振幅:
驱动力的频率等于振动物体的固有频率时,振幅最大;驱动力的频率跟固有频率相差越大,振幅越小
f驱= f固时,振幅有最大值
f驱与 f固差别越大时,振幅越小
(共振)
