高二物理选修3-4 第11章章末习题含答案 (人教版)
文档属性
| 名称 | 高二物理选修3-4 第11章章末习题含答案 (人教版) |  | |
| 格式 | zip | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-27 20:34:44 | ||
图片预览




文档简介
第11章章末习题
一.选择题(共1小题)
1.有一天体半径为地球半径的4倍,平均密度与地球相同.则在地球表面上走时准确的摆钟移到该天体的表面,秒针走一圈的实际时间为( )
A.min B.min C.min D.2min
二.多选题(共1小题)
2.如图所示,在倾角为θ的固定光滑斜面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,C为一固定的挡板,小店让一质量为m的物体D从距A为L的位置由静止释放,D和A相碰后立即粘为一体,之后在斜面上做简谐运动,在简谐运动过程中,物体B对C的最小弹力为mgsinθ,则( )
A.简谐运动的振幅为
B.简谐运动的振幅为
C.B对C的最大弹力
D.B对C的最大弹力
三.填空题(共1小题)
3.如图所示,一质量为M的无底木箱,放在水平地面上,一轻质弹簧一端悬于木箱的上边,另一端挂着用细线连接在一起的两物体A和B,mA=mB=m.剪断A、B间的细线后,A做简谐运动,则当A振动到最高点时,木箱对地面的压力为 .
四.计算题(共1小题)
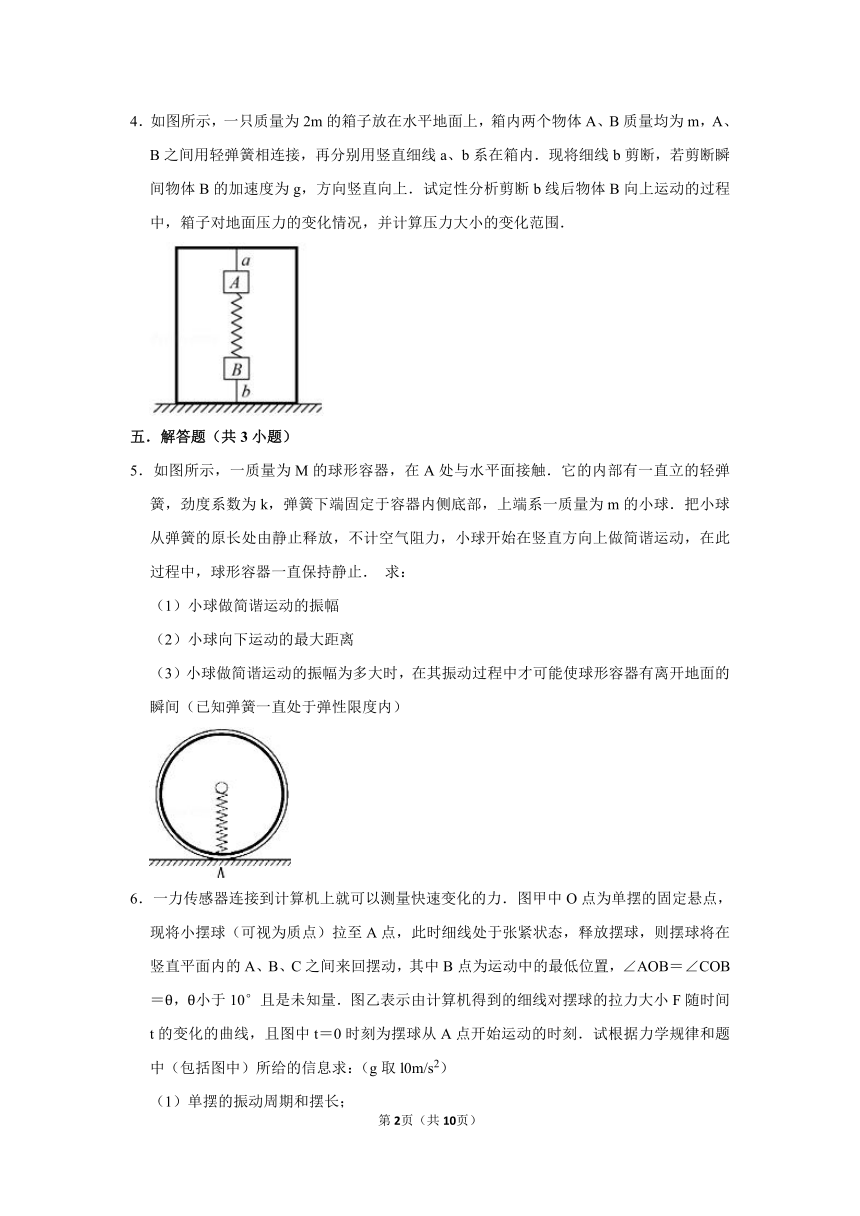
4.如图所示,一只质量为2m的箱子放在水平地面上,箱内两个物体A、B质量均为m,A、B之间用轻弹簧相连接,再分别用竖直细线a、b系在箱内.现将细线b剪断,若剪断瞬间物体B的加速度为g,方向竖直向上.试定性分析剪断b线后物体B向上运动的过程中,箱子对地面压力的变化情况,并计算压力大小的变化范围.
五.解答题(共3小题)
5.如图所示,一质量为M的球形容器,在A处与水平面接触.它的内部有一直立的轻弹簧,劲度系数为k,弹簧下端固定于容器内侧底部,上端系一质量为m的小球.把小球从弹簧的原长处由静止释放,不计空气阻力,小球开始在竖直方向上做简谐运动,在此过程中,球形容器一直保持静止. 求:
(1)小球做简谐运动的振幅
(2)小球向下运动的最大距离
(3)小球做简谐运动的振幅为多大时,在其振动过程中才可能使球形容器有离开地面的瞬间(已知弹簧一直处于弹性限度内)
6.一力传感器连接到计算机上就可以测量快速变化的力.图甲中O点为单摆的固定悬点,现将小摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的A、B、C之间来回摆动,其中B点为运动中的最低位置,∠AOB=∠COB=θ,θ小于10°且是未知量.图乙表示由计算机得到的细线对摆球的拉力大小F随时间t的变化的曲线,且图中t=0时刻为摆球从A点开始运动的时刻.试根据力学规律和题中(包括图中)所给的信息求:(g取l0m/s2)
(1)单摆的振动周期和摆长;
(2)摆球的质量;
(3)摆球运动过程中的最大速度.
7.摆长为l的单摆在平衡位置O的左右做摆角小于5°的简谐运动,当摆球经过平衡位置O(O在A点正上方)向右运动的同时,另一个以速度v在光滑水平面运动的小滑块,恰好经过A点向右运动,如图8所示,小滑块与竖直挡板P碰撞后以原来的速率返回,略去碰撞所用时间,试问:
(1)A、P间的距离满足什么条件,才能使滑块刚好返回A点时,摆球也同时到达O点且向左运动?
(2)AP间的最小距离是多少?
第11章章末习题
参考答案与试题解析
一.选择题(共1小题)
1.有一天体半径为地球半径的4倍,平均密度与地球相同.则在地球表面上走时准确的摆钟移到该天体的表面,秒针走一圈的实际时间为( )
A.min B.min C.min D.2min
【解答】解:星球的质量M=ρV=ρ物体在星球表面所受的万有引力等于重力,所以有:
mg=
则有:g=
所以该星球的表面重力加速度与地球表面的重力加速度之比为:
根据单摆的周期公式有:T=
当T地=1min时,T星=min
即在地球表面秒针走一圈的周期是1min,则在该星球上的秒针走一圈的时间为min。
故选:A。
二.多选题(共1小题)
2.如图所示,在倾角为θ的固定光滑斜面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,C为一固定的挡板,小店让一质量为m的物体D从距A为L的位置由静止释放,D和A相碰后立即粘为一体,之后在斜面上做简谐运动,在简谐运动过程中,物体B对C的最小弹力为mgsinθ,则( )
A.简谐运动的振幅为
B.简谐运动的振幅为
C.B对C的最大弹力
D.B对C的最大弹力
【解答】解:当弹力等于AD的重力的分力时AD处于平衡状态,由kx=2mgsinθ可知,平衡位置时弹簧的形变量为x0=,处压缩状态;
当B对C弹力最小时,对B分析,则有mgsinθ=Kx+mgsinθ;
故弹簧应伸长达最大位移处,此时形变量x=,此时弹簧处于伸长状态;
故简谐运动的振幅为A=x+x0=+=;故B正确,A错误;
当AD运动到最低点时,B对C的弹力最大;由对称性可知,此时弹簧的形变量为A+x0=+=;
此时弹力为F=k(A+x0)=;
B对C的弹力为F+mgsinθ=;故C错误,D正确;
故选:BD。
三.填空题(共1小题)
3.如图所示,一质量为M的无底木箱,放在水平地面上,一轻质弹簧一端悬于木箱的上边,另一端挂着用细线连接在一起的两物体A和B,mA=mB=m.剪断A、B间的细线后,A做简谐运动,则当A振动到最高点时,木箱对地面的压力为 Mg .
【解答】解:剪断A、B间细线瞬间,A的加速度大小为 a==g,方向竖直向上.
根据简谐振动的对称性,可知A在最高点时其加速度大小为g,方向竖直向下,设弹簧的弹力为F,方向向下.
根据牛顿第二定律得:F+mg=ma=mg,则F=0
故此时木箱受重力、地面支持力,根据平衡条件,有:地面对木箱的支持力N=Mg
由牛顿第三定律知,木箱对地面的压力为Mg.
故答案为:Mg.
四.计算题(共1小题)
4.如图所示,一只质量为2m的箱子放在水平地面上,箱内两个物体A、B质量均为m,A、B之间用轻弹簧相连接,再分别用竖直细线a、b系在箱内.现将细线b剪断,若剪断瞬间物体B的加速度为g,方向竖直向上.试定性分析剪断b线后物体B向上运动的过程中,箱子对地面压力的变化情况,并计算压力大小的变化范围.
【解答】解:现将细线b剪断,B将做简谐振动,在最低点:F1﹣mg=mg
所以:F1=2mg
B做简谐运动,根据对称性,最高点的加速度为g,竖直向下,则:F2﹣mg=mg
所以F2=0
可知B上升的过程中A始终不动;
以木箱与A组成的系统为研究对象,由于A始终不动,所以木箱与A组成的系统始终处于平衡状态,当B在最低点时:
FN1=2mg+mg+F1=5mg
当B在最高点时:FN2=2mg+mg+F2=3mg
故箱子受到的地面的支持力最大为5mg,最小为3mg,
由牛顿第三定律可知,木箱对地面的压力最大为5mg,最小为3mg;
答:压力大小的变化范围是5mg到3mg.
五.解答题(共3小题)
5.如图所示,一质量为M的球形容器,在A处与水平面接触.它的内部有一直立的轻弹簧,劲度系数为k,弹簧下端固定于容器内侧底部,上端系一质量为m的小球.把小球从弹簧的原长处由静止释放,不计空气阻力,小球开始在竖直方向上做简谐运动,在此过程中,球形容器一直保持静止. 求:
(1)小球做简谐运动的振幅
(2)小球向下运动的最大距离
(3)小球做简谐运动的振幅为多大时,在其振动过程中才可能使球形容器有离开地面的瞬间(已知弹簧一直处于弹性限度内)
【解答】解:(1)从释放点到平衡位置的距离就是小球的振幅,为:A=
(2)根据简谐运动关于平衡位置对称,可知振子向下运动的最大距离
S=2A=
(3)球形容器要离开地面,最容易发生在小球运动到最高点时,此时弹簧处于拉伸状态,且拉力的大小至少等于容器的重力,即
F=Mg
则弹簧的伸长量 x2=
小球振动时的平衡位置居于弹簧原长下方距离为:x1=
所以,满足条件的最小振幅为:A′=x1+x2=
答:
(1)小球做简谐运动的振幅是.
(2)小球向下运动的最大距离是.
(3)小球做简谐运动的振幅为时,在其振动过程中才可能使球形容器有离开地面的瞬间.
6.一力传感器连接到计算机上就可以测量快速变化的力.图甲中O点为单摆的固定悬点,现将小摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的A、B、C之间来回摆动,其中B点为运动中的最低位置,∠AOB=∠COB=θ,θ小于10°且是未知量.图乙表示由计算机得到的细线对摆球的拉力大小F随时间t的变化的曲线,且图中t=0时刻为摆球从A点开始运动的时刻.试根据力学规律和题中(包括图中)所给的信息求:(g取l0m/s2)
(1)单摆的振动周期和摆长;
(2)摆球的质量;
(3)摆球运动过程中的最大速度.
【解答】解:(1)由图乙得小球在A、C之间做简谐运动的周期:
①
由单摆振动周期公式,得到单摆摆线长:
代入数据,得:
L=0.4m ②
(2)(3)在最高点A,有:
Fmin=mgcosθ,式中Fmin=0.495N ③
在最低点B,有:
④
从A到B过程中,滑块机械能守恒,故:
⑤
滑块机械能:
⑥
由②③④⑤⑥解得:
cosθ=0.99
m=0.05kg
vmax=0.283m/s
答:(1)单摆的振动周期为0.4πs,摆长为0.4m;
(2)摆球的质量为0.05kg;
(3)摆动过程中的速度为0.283m/s
7.摆长为l的单摆在平衡位置O的左右做摆角小于5°的简谐运动,当摆球经过平衡位置O(O在A点正上方)向右运动的同时,另一个以速度v在光滑水平面运动的小滑块,恰好经过A点向右运动,如图8所示,小滑块与竖直挡板P碰撞后以原来的速率返回,略去碰撞所用时间,试问:
(1)A、P间的距离满足什么条件,才能使滑块刚好返回A点时,摆球也同时到达O点且向左运动?
(2)AP间的最小距离是多少?
【解答】解:(1)小滑块做匀速直线运动的往返时间为t1,有:t1=
单摆做简谐运动回到O点且向左运动所需时间为t2,有:t2=+nT(n=0,1,2…),
其中T=2π,
由题意可知:t1=t2,所以有:=+nT,
即为:x=(+n)T=(2n+1)T=(2n+1)?2π= (n=0,1,2…)。
(2)n=0时,A间的距离最小,为:xmin= 。
答:(1)A、P间的距离满足x= (n=0,1,2…),才能使滑块刚好返回A点时,摆球也同时到达O点且向左运动;
(2)AP间的最小距离是 。
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/2/24 8:57:27;用户:石永生;邮箱:42254019@qq.com;学号:21018404
第1页(共1页)
