北师大版七年级数学下册 2.1两条直线的位置关系(第1课时 共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.1两条直线的位置关系(第1课时 共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 32.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 16:54:56 | ||
图片预览






文档简介
(共23张PPT)
1.直线的特征是什么?
2.直线的表示方法有哪些?
复习回顾
那么同一平面内的两条直线都有哪些位置关系呢?
第二章 平行线与相交线
2.1 两条直线的位置关系(1)
观察下列生活中的图片,说一说直线与直线的位置关系.
情境引入
情境引入
情境引入
情境引入
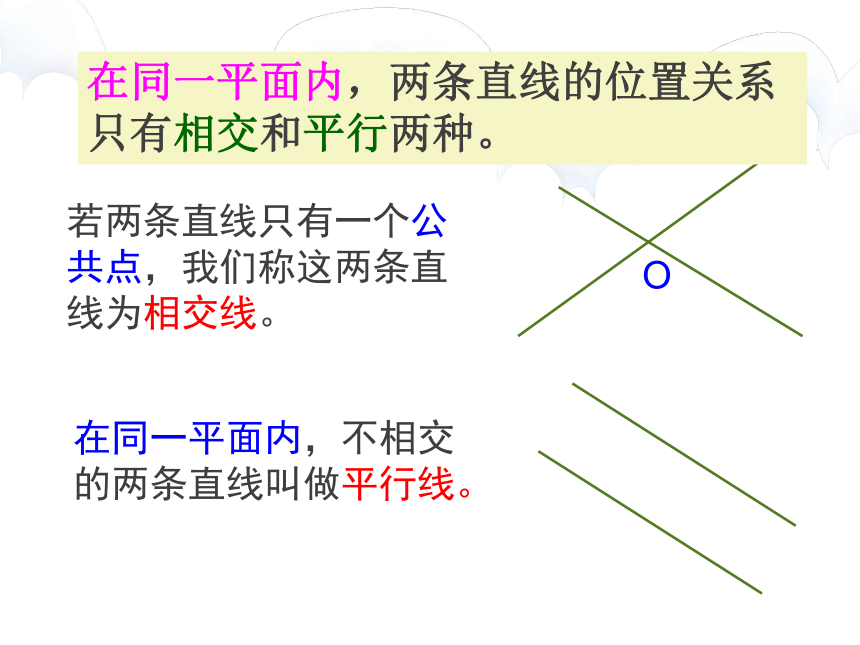
若两条直线只有一个公共点,我们称这两条直线为相交线。
O
在同一平面内,不相交的两条直线叫做平行线。
在同一平面内,两条直线的位置关系只有相交和平行两种。
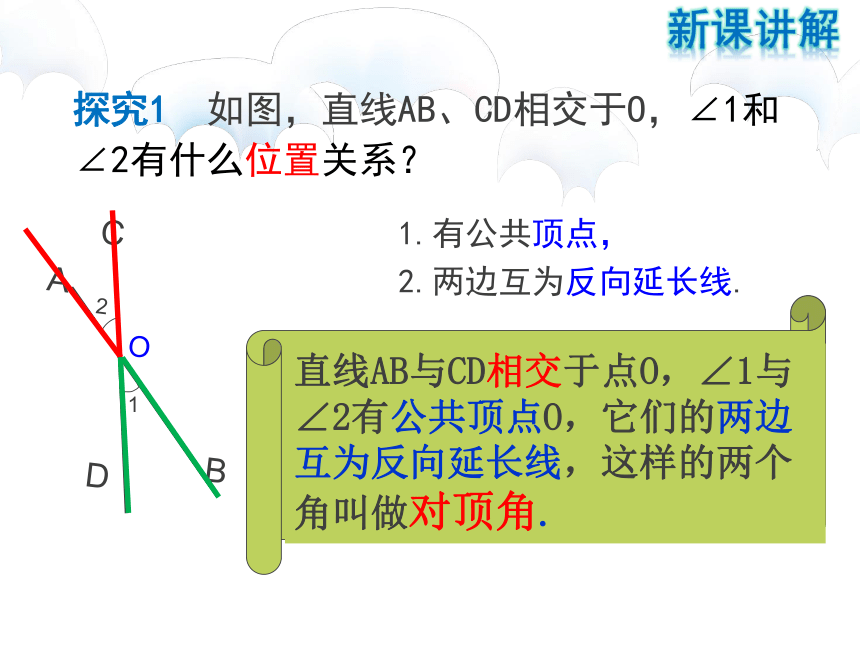
探究1 如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
1.有公共顶点,
2.两边互为反向延长线.
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
新课讲解
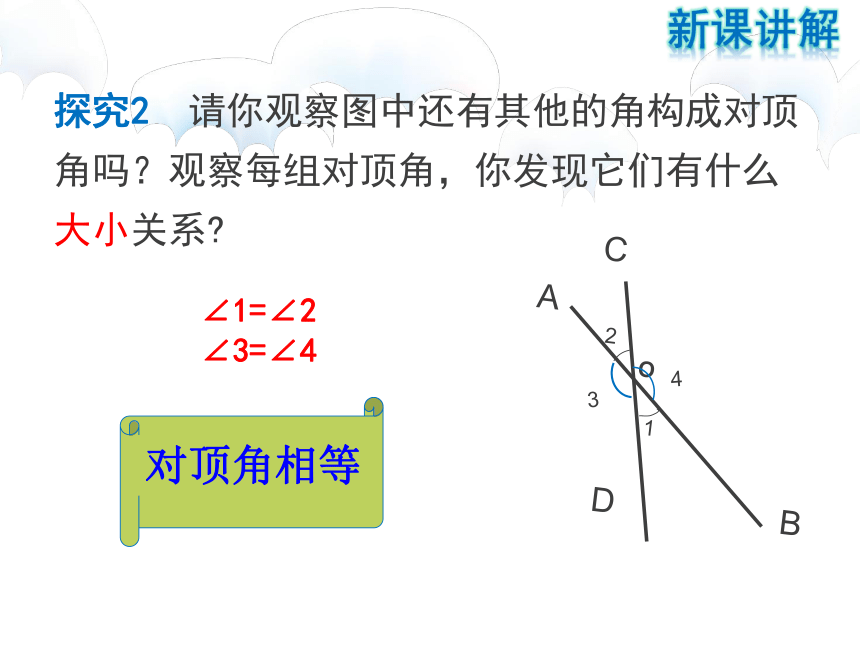
探究2 请你观察图中还有其他的角构成对顶角吗?观察每组对顶角,你发现它们有什么大小关系?
∠1=∠2
∠3=∠4
对顶角相等
新课讲解
2
1
A
B
C
D
O
3
4
下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
练习
探究3 在下图中,∠1与∠3有什么数量关系?
2
1
A
B
C
D
O
3
4
∠1+∠3=180°
如果两个角的和是900,那么称这两个角互为余角。
如果两个角的和是1800,那么称这两个角互为补角。
类似地,
1
2
∠1+∠2=90°
小试牛刀
判断:下列说法正确的有 。(填序号)
①若∠1+∠2+∠3=180?,则∠1、∠2、∠3互补
②若∠A=40?26′,则∠A的余角=49?34′
③一个角的补角必为钝角。
②
图1
N
2
D
C
O
1
3
4
A
B
图2
探究4 如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
新课讲解
1
2
小组合作交流,解决下列问题:在图2中
问题1 哪些角互为补角?哪些角互为余角?
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
已知:∠1=∠2.
∠DON=∠CON=900
问题2 ∠3与∠4有什么关系?为什么?
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
问题3 ∠AOC与∠BOD有什么关系?为什么?
1. ①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1=_____,理由是_ __________.
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1=______,理由是_ _________.
2. 如图2.1—11已知:直线AB与CD交于点O,∠COE=900,回答下列问题:
(1)∠AOE的余角是_ ________;补角是_________。
(2)∠AOD的余角是________;补角是_ _______;
对顶角是________。
随堂即练
∠3
∠3
同角的余角相等
同角的补角相等
∠COB和∠DOA
∠BOE
∠AOE
∠COA和∠DOB
B
A
C
D
O
E
∠BOC
3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
随堂即练
4.若一个角的补角等于它的余角的4倍,求这个角的度数.
随堂即练
5.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
随堂即练
课堂小结
本节课你都有哪些收获?还有那些疑问?
课后作业
课本P40 习题2.1
1T、3T、4T
1.直线的特征是什么?
2.直线的表示方法有哪些?
复习回顾
那么同一平面内的两条直线都有哪些位置关系呢?
第二章 平行线与相交线
2.1 两条直线的位置关系(1)
观察下列生活中的图片,说一说直线与直线的位置关系.
情境引入
情境引入
情境引入
情境引入
若两条直线只有一个公共点,我们称这两条直线为相交线。
O
在同一平面内,不相交的两条直线叫做平行线。
在同一平面内,两条直线的位置关系只有相交和平行两种。
探究1 如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
1.有公共顶点,
2.两边互为反向延长线.
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
新课讲解
探究2 请你观察图中还有其他的角构成对顶角吗?观察每组对顶角,你发现它们有什么大小关系?
∠1=∠2
∠3=∠4
对顶角相等
新课讲解
2
1
A
B
C
D
O
3
4
下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
练习
探究3 在下图中,∠1与∠3有什么数量关系?
2
1
A
B
C
D
O
3
4
∠1+∠3=180°
如果两个角的和是900,那么称这两个角互为余角。
如果两个角的和是1800,那么称这两个角互为补角。
类似地,
1
2
∠1+∠2=90°
小试牛刀
判断:下列说法正确的有 。(填序号)
①若∠1+∠2+∠3=180?,则∠1、∠2、∠3互补
②若∠A=40?26′,则∠A的余角=49?34′
③一个角的补角必为钝角。
②
图1
N
2
D
C
O
1
3
4
A
B
图2
探究4 如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
新课讲解
1
2
小组合作交流,解决下列问题:在图2中
问题1 哪些角互为补角?哪些角互为余角?
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
已知:∠1=∠2.
∠DON=∠CON=900
问题2 ∠3与∠4有什么关系?为什么?
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
问题3 ∠AOC与∠BOD有什么关系?为什么?
1. ①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1=_____,理由是_ __________.
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1=______,理由是_ _________.
2. 如图2.1—11已知:直线AB与CD交于点O,∠COE=900,回答下列问题:
(1)∠AOE的余角是_ ________;补角是_________。
(2)∠AOD的余角是________;补角是_ _______;
对顶角是________。
随堂即练
∠3
∠3
同角的余角相等
同角的补角相等
∠COB和∠DOA
∠BOE
∠AOE
∠COA和∠DOB
B
A
C
D
O
E
∠BOC
3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
随堂即练
4.若一个角的补角等于它的余角的4倍,求这个角的度数.
随堂即练
5.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
随堂即练
课堂小结
本节课你都有哪些收获?还有那些疑问?
课后作业
课本P40 习题2.1
1T、3T、4T
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
