人教版八年级数学下册 19.1函数同步练习题解析版
文档属性
| 名称 | 人教版八年级数学下册 19.1函数同步练习题解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 154.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 21:34:56 | ||
图片预览



文档简介
人教版八年级下册19.1《函数》同步练习题
一.选择题(共10小题)
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.一个圆柱的高h为10cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中( )
A.r是因变量,V是自变量 B.r是自变量,V是因变量
C.r是自变量,h是因变量 D.h是自变量,V是因变量
3.下列平面直角坐标系中的图象,不能表示y是x的函数是( )
A.B.C.D.
4.变量x、y有如下的关系,其中y是x的函数的是( )
A.y2=8x B.|y|=x C.y= D.x=y4
5.函数y=+(x﹣5)﹣2中自变量x的取值范围是( )
A.x≥3且≠5 B.x>3且x≠5 C.x<3且x≠5 D.x≤3且x≠5
6.在平面直角坐标系中,点P(x,y)在第一象限内,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S,S与x之间的函数关系式是( )
A.S=﹣x+8(0<x<8) B.S=﹣3x+24(0<x<8)
C.S=﹣3x+12(0<x<4) D.S=﹣x+8(0<x<8)
7.如图,射线l甲、l乙分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的函数关系,则他们行进的速度关系是( )
A.甲比乙快 B.乙比甲快 C.甲、乙同速 D.不一定
8.某数学兴趣小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表),下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
声速m/s 318 324 330 336 342 348
A.在这个变化中自变量是温度,因变量是声速
B.当温度每升高10C,声速增加6m/s
C.当空气温度为20℃,5s的时间可以传播1740m
D.温度越高声速越快
9.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
10.如图是一个运算程序的示意图,若输出y的值为2,则输入x的值可能为( )
A.3 B.±1 C.1或3 D.±1或3
二.填空题(共3小题)
11.函数的定义域是 .
12.n支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m与球队数n之间的关系式 .
13.某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长,其中正确的结论序号是 .
三.解答题(共5小题)
14.在一次实验中,马达同学把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上表反应了哪两个变量之间的关系,并指出谁是自变量,谁是因变量.
(2)当悬挂物体的重量为3千克时,弹簧长 ;不挂重物时弹簧长 .
(3)弹簧长度y与所挂物体质量x之间的关系可以用式子表示为: .
(4)求挂10kg物体时弹簧长度及弹簧长36cm时所挂物体的重量.
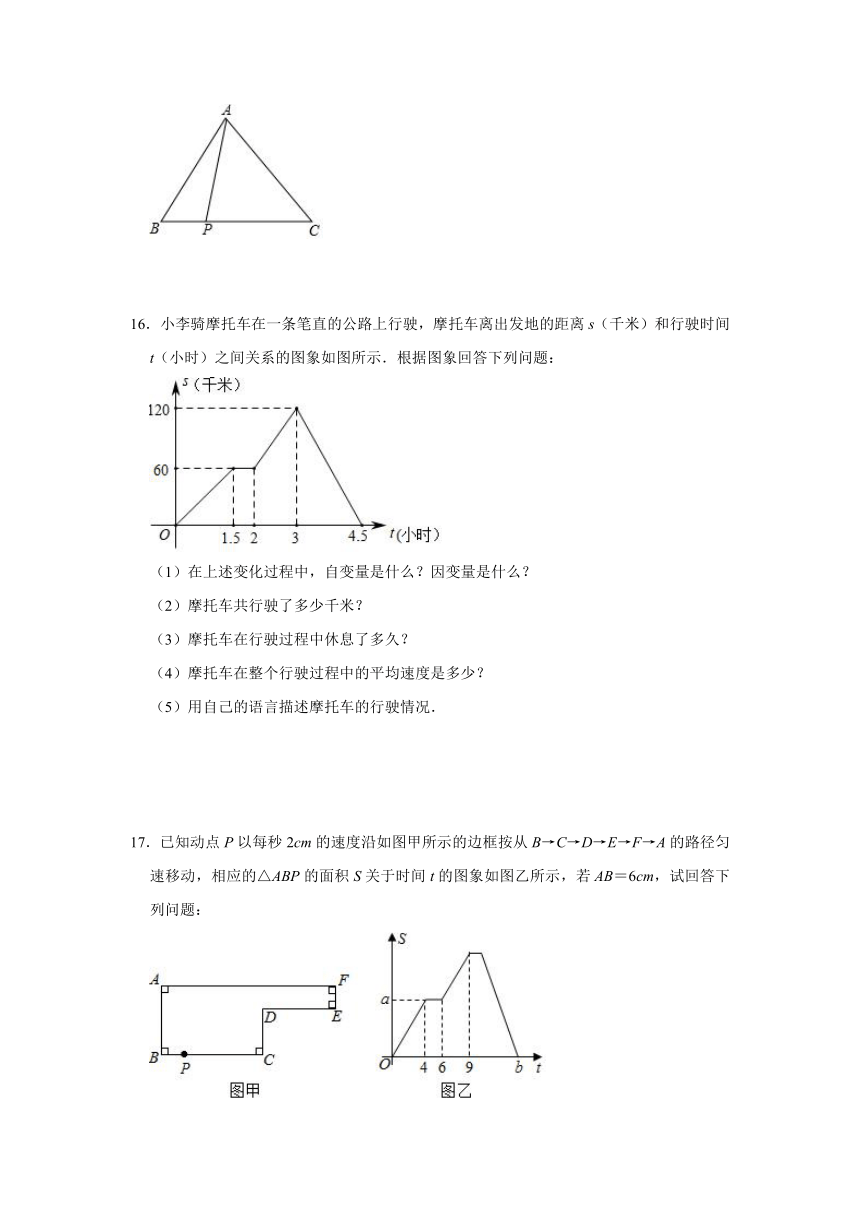
15.已知△ABC的面积是12cm2,BC=6cm,在BC边上有一动点P,连接P,设BP为xcm.△ABP的面积为ycm2,
(1)求y与x之间的关系式
(2)用表格表示当从1到6时(每次增加1),y的对应值.
(3)当x=0时,y的值等于多少?此时说明了什么?
16.小李骑摩托车在一条笔直的公路上行驶,摩托车离出发地的距离s(千米)和行驶时间t(小时)之间关系的图象如图所示.根据图象回答下列问题:
(1)在上述变化过程中,自变量是什么?因变量是什么?
(2)摩托车共行驶了多少千米?
(3)摩托车在行驶过程中休息了多久?
(4)摩托车在整个行驶过程中的平均速度是多少?
(5)用自己的语言描述摩托车的行驶情况.
17.已知动点P以每秒2cm的速度沿如图甲所示的边框按从B→C→D→E→F→A的路径匀速移动,相应的△ABP的面积S关于时间t的图象如图乙所示,若AB=6cm,试回答下列问题:
(1)求出图甲中BC的长和多边形ABCDEF的面积;
(2)直接写出图乙中a和b的值.
18.如图(1),已知点A(4,0),点P(x,y)在第一象限,且x+y=6.设△OPA面积为S
(1)求S关于x的函数关系式,并写出x的取值范围.
(2)当S=6时,求P点的坐标;
(3)在图(2)中画出S关于x的函数图象.
参考答案
一.选择题(共10小题)
1.【解答】解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:B.
2.【解答】解:一个圆柱的高h为10cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中
r是自变量,V是因变量,
故选:B.
3.【解答】解:A、能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项符合题意;
C、能表示y是x的函数,故此选项不合题意;
D、能表示y是x的函数,故此选项不合题意;
故选:B.
4.【解答】解:A、y2=8x,y不是x的函数,故此选项错误;
B、|y|=x,y不是x的函数,故此选项错误;
C、y=,y是x的函数,故此选项正确;
D、x=y4,y不是x的函数,故此选项错误;
故选:C.
5.【解答】解:依题意有x﹣3>0且x﹣5≠0,
解得:x>3且x≠5.
故选:B.
6.【解答】解:∵点P(x,y)在第一象限内,且x+y=8,
∴y=8﹣x(0<x<8).
∵点A的坐标为(6,0),点O的坐标为(0,0),
∴S=OP?y=×6y=﹣3x+24(0<x<8).
故选:B.
7.【解答】解:根据图象越陡峭,速度越快;可得甲比乙快.
故选:A.
8.【解答】解:A、∵在这个变化中,自变量是温度,因变量是声速,
∴选项A正确;
B、∵324﹣318=6(m/s),330﹣324=6(m/s),336﹣330=6(m/s),342﹣336=6(m/s),348﹣342=6(m/s),
∴当温度每升高10℃,声速增加6m/s,
∴选项B正确;
C、∵342×5=1710(m),
∴当空气温度为20℃时,声音5s可以传播1710m,
∴选项C错误;
D、∵根据数据表,可得温度越高,声速越快,
∴选项D正确.
故选:C.
9.【解答】解:汽车从出发地到目的地走了140千米,又回到出发地因而共行驶了280千米,故①错误;
汽车在行驶途中停留了4﹣3=1小时,故②正确;
汽车在整个行驶过程中的平均速度为:280÷(9﹣1)=35(千米/时),故③错误;
汽车出发后6小时至9小时之间行驶的速度不变,故④错误.
综上所述,正确的只有②.
故选:A.
10.【解答】解:当x+1=2时,x=1,不符合x≤0;
当x2+1=2时,x=±1,此时x=1符合;
当=2时,x=3,此时符合;
∴x=3或x=1,
故选:C.
二.填空题(共3小题)
11.【解答】解:依题得:,
解得.
故答案为:.
12.【解答】解:m=n(n﹣1)=n2﹣n,
故答案为:m=n2﹣n
13.【解答】解:①由纵坐标看出1月份的增长率是10%,2月份的增长率是5%,3月份的增长率是3%,故①说法正确;
②2月份比1月份增长5%,故②说法错误;
③1月份的增长率是10%,2月份的增长率是5%,3月份的增长率是3%,故③说法正确;
故答案为:①③.
三.解答题(共5小题)
14.【解答】解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24cm;当不挂重物时,弹簧长18cm;
故答案为:24cm;18cm;
(3)弹簧长度y与所挂物体质量x之间的关系可以用式子表示为:y=2x+18(x≥0);
故答案为:y=2x+18(x≥0);
(4)当x=10kg时,y=2x+18=2×10+18=38cm;当y=36cm时,即36=2x+18,
∴x=9,
即挂10kg物体时弹簧长度是38kg,弹簧长36cm时所挂物体的重量是9kg.
15.【解答】解:(1)△ABC的面积是12cm2,BC=6cm,则在BC边上的高为4cm,
∴△ABP的面积为:y=x×4=2x,(0≤x≤6)
(2)用表格表示:
(3)当x=0时,y=0,说明此时点P与点B重合.
16.【解答】解:(1)根据定义:行驶时间t为自变量,摩托车离出发地的距离s为因变量;
(2)从图象可以看出:摩托车共行驶的距离s最大为120千米,即摩托车共行驶了240千米;
(3)摩托车在行驶过程中休息,t从1.5到2,共0.5个小时;
(4)摩托车在整个行驶过程中,行驶的总时间为4小时,距离为240千米,故平均速度为240÷4=60(千米/小时);
(5)摩托车以60千米/小时行驶了1.5小时,然后休息0.5小时,再以60千米/小时行驶了1小时到达目的地,最后以80千米/小时的速度返回.
17.【解答】解:(1)由图象可得BC=4×2=8cm,CD=2×2=4cm,DE=3×2=6cm,EF=6﹣4=2cm,
∴多边形ABCDEF的面积=6×8+6×2=60cm2,
(2)由题意可得:a=6×8=24,b==17
18.【解答】解:∵S=OA?yP
=×4×(6﹣x)
=12﹣2x.
其中0<x<6;
(2)当S=6时,12﹣2x=6,
解得x=3.
把x=3代入x+y=6,得y=3,
∴P点的坐标为(3,3);
(3)如图,
即为S关于x的函数图象.
