华东师大版九年级数学下册第27章 应用扇形面积公式求阴影部分的面积同步练习(含答案)
文档属性
| 名称 | 华东师大版九年级数学下册第27章 应用扇形面积公式求阴影部分的面积同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 00:00:00 | ||
图片预览




文档简介
华东师大版九年级数学下册第27章 应用扇形面积公式求阴影部分的面积
一、选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=( )
A.2π B.π C.π D.π
2.如图所示,边长为a的正方形中阴影部分的面积为( )
A.a2-π()2 B.a2-πa2
C.a2-πa D.a2-2πa
3.如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连结OB,OD,则图中阴影部分的面积为( )
A.2π B.4π C.8π D.16π
4.如图,正方形ABCD的边长为8,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.32 B.2π
C.10π+2 D.8π+1
5.如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,B,E是以AD为直径的半圆O的三等分点,的长为π,∠C=90°,则图中阴影部分的面积为( )
A. B.
C.- D.-
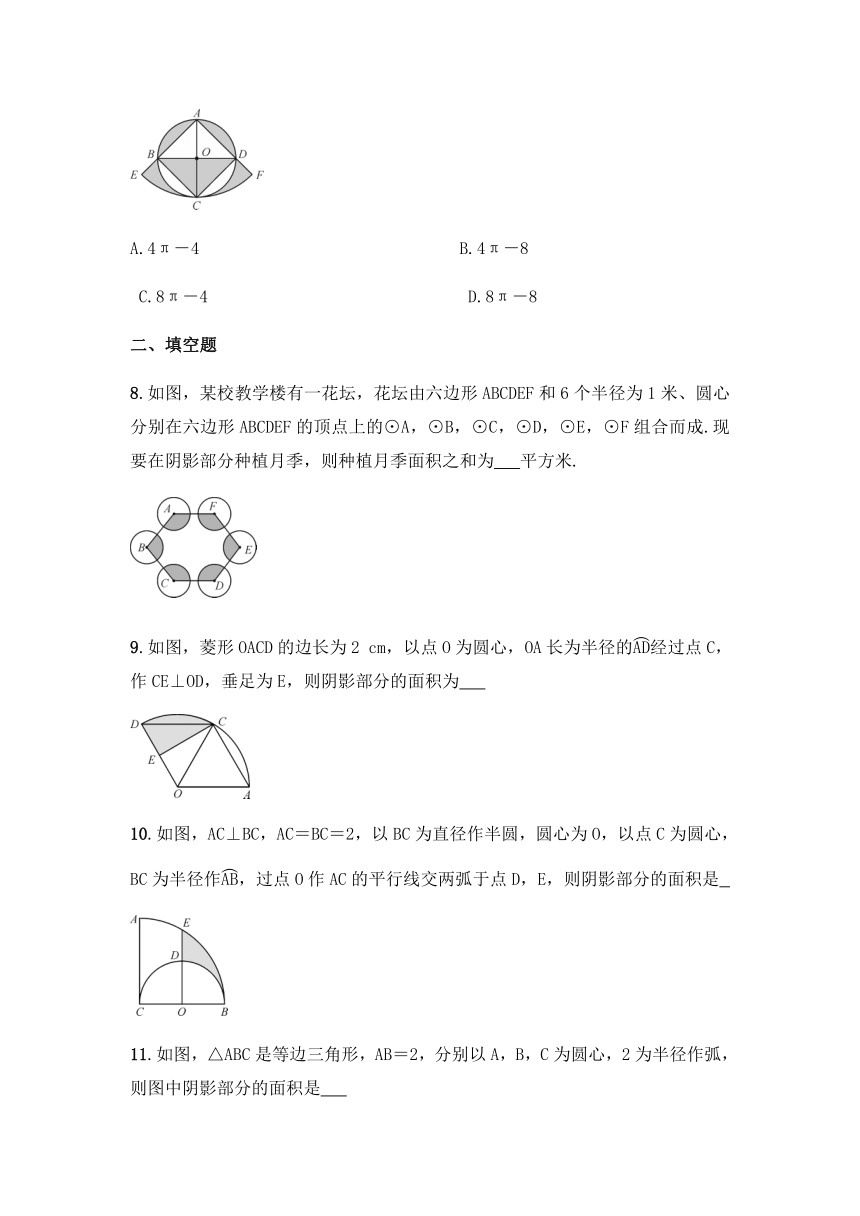
7.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为( )
A.4π-4 B.4π-8
C.8π-4 D.8π-8
二、填空题
8.如图,某校教学楼有一花坛,花坛由六边形ABCDEF和6个半径为1米、圆心分别在六边形ABCDEF的顶点上的⊙A,⊙B,⊙C,⊙D,⊙E,⊙F组合而成.现要在阴影部分种植月季,则种植月季面积之和为 平方米.
9.如图,菱形OACD的边长为2 cm,以点O为圆心,OA长为半径的经过点C,作CE⊥OD,垂足为E,则阴影部分的面积为
10.如图,AC⊥BC,AC=BC=2,以BC为直径作半圆,圆心为O,以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D,E,则阴影部分的面积是
11.如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,2为半径作弧,则图中阴影部分的面积是
12.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为,则图中阴影部分的面积为 .
13.如图,将半径为6的圆形纸片分别沿AB,BC折叠,若和折后都经过圆心O,则阴影部分的面积是 .(结果保留π)
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是 .
三、解答题
15.如图,在△ABC中,AB=4,AC=2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
参考答案
一、选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=(B)
A.2π B.π C.π D.π
2.如图所示,边长为a的正方形中阴影部分的面积为(A)
A.a2-π()2 B.a2-πa2
C.a2-πa D.a2-2πa
3.如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连结OB,OD,则图中阴影部分的面积为(B)
A.2π B.4π C.8π D.16π
4.如图,正方形ABCD的边长为8,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是(A)
A.32 B.2π
C.10π+2 D.8π+1
5.如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为(A)
A. B. C. D.
6.如图,B,E是以AD为直径的半圆O的三等分点,的长为π,∠C=90°,则图中阴影部分的面积为(C)
A. B.
C.- D.-
7.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为(A)
A.4π-4 B.4π-8
C.8π-4 D.8π-8
二、填空题
8.如图,某校教学楼有一花坛,花坛由六边形ABCDEF和6个半径为1米、圆心分别在六边形ABCDEF的顶点上的⊙A,⊙B,⊙C,⊙D,⊙E,⊙F组合而成.现要在阴影部分种植月季,则种植月季面积之和为2π平方米.
9.如图,菱形OACD的边长为2 cm,以点O为圆心,OA长为半径的经过点C,作CE⊥OD,垂足为E,则阴影部分的面积为(π-)cm2.
10.如图,AC⊥BC,AC=BC=2,以BC为直径作半圆,圆心为O,以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D,E,则阴影部分的面积是π-.
11.如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,2为半径作弧,则图中阴影部分的面积是2π-3.
12.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为,则图中阴影部分的面积为π-.
13.如图,将半径为6的圆形纸片分别沿AB,BC折叠,若和折后都经过圆心O,则阴影部分的面积是12π.(结果保留π)
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是π-2.
三、解答题
15.如图,在△ABC中,AB=4,AC=2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
解:(1)相切.
理由:∵22+(2)2=16=42,
∴AC2+BC2=AB2.
∴∠ACB=90°.
∴以BC为直径的圆与AC所在的直线相切.
(2)∵在Rt△ABC中,cosA==,
∴∠A=60°.
∴S阴影=S半圆-(S△ABC-S扇形ACE)
=×π×()2-(×2×2-×π×22)
=-2.
一、选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=( )
A.2π B.π C.π D.π
2.如图所示,边长为a的正方形中阴影部分的面积为( )
A.a2-π()2 B.a2-πa2
C.a2-πa D.a2-2πa
3.如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连结OB,OD,则图中阴影部分的面积为( )
A.2π B.4π C.8π D.16π
4.如图,正方形ABCD的边长为8,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.32 B.2π
C.10π+2 D.8π+1
5.如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,B,E是以AD为直径的半圆O的三等分点,的长为π,∠C=90°,则图中阴影部分的面积为( )
A. B.
C.- D.-
7.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为( )
A.4π-4 B.4π-8
C.8π-4 D.8π-8
二、填空题
8.如图,某校教学楼有一花坛,花坛由六边形ABCDEF和6个半径为1米、圆心分别在六边形ABCDEF的顶点上的⊙A,⊙B,⊙C,⊙D,⊙E,⊙F组合而成.现要在阴影部分种植月季,则种植月季面积之和为 平方米.
9.如图,菱形OACD的边长为2 cm,以点O为圆心,OA长为半径的经过点C,作CE⊥OD,垂足为E,则阴影部分的面积为
10.如图,AC⊥BC,AC=BC=2,以BC为直径作半圆,圆心为O,以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D,E,则阴影部分的面积是
11.如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,2为半径作弧,则图中阴影部分的面积是
12.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为,则图中阴影部分的面积为 .
13.如图,将半径为6的圆形纸片分别沿AB,BC折叠,若和折后都经过圆心O,则阴影部分的面积是 .(结果保留π)
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是 .
三、解答题
15.如图,在△ABC中,AB=4,AC=2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
参考答案
一、选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=(B)
A.2π B.π C.π D.π
2.如图所示,边长为a的正方形中阴影部分的面积为(A)
A.a2-π()2 B.a2-πa2
C.a2-πa D.a2-2πa
3.如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连结OB,OD,则图中阴影部分的面积为(B)
A.2π B.4π C.8π D.16π
4.如图,正方形ABCD的边长为8,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是(A)
A.32 B.2π
C.10π+2 D.8π+1
5.如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为(A)
A. B. C. D.
6.如图,B,E是以AD为直径的半圆O的三等分点,的长为π,∠C=90°,则图中阴影部分的面积为(C)
A. B.
C.- D.-
7.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为(A)
A.4π-4 B.4π-8
C.8π-4 D.8π-8
二、填空题
8.如图,某校教学楼有一花坛,花坛由六边形ABCDEF和6个半径为1米、圆心分别在六边形ABCDEF的顶点上的⊙A,⊙B,⊙C,⊙D,⊙E,⊙F组合而成.现要在阴影部分种植月季,则种植月季面积之和为2π平方米.
9.如图,菱形OACD的边长为2 cm,以点O为圆心,OA长为半径的经过点C,作CE⊥OD,垂足为E,则阴影部分的面积为(π-)cm2.
10.如图,AC⊥BC,AC=BC=2,以BC为直径作半圆,圆心为O,以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D,E,则阴影部分的面积是π-.
11.如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,2为半径作弧,则图中阴影部分的面积是2π-3.
12.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为,则图中阴影部分的面积为π-.
13.如图,将半径为6的圆形纸片分别沿AB,BC折叠,若和折后都经过圆心O,则阴影部分的面积是12π.(结果保留π)
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是π-2.
三、解答题
15.如图,在△ABC中,AB=4,AC=2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
解:(1)相切.
理由:∵22+(2)2=16=42,
∴AC2+BC2=AB2.
∴∠ACB=90°.
∴以BC为直径的圆与AC所在的直线相切.
(2)∵在Rt△ABC中,cosA==,
∴∠A=60°.
∴S阴影=S半圆-(S△ABC-S扇形ACE)
=×π×()2-(×2×2-×π×22)
=-2.
