2020春北师大版七下数学4.2图形的全等同步测试(无答案)
文档属性
| 名称 | 2020春北师大版七下数学4.2图形的全等同步测试(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 16:09:19 | ||
图片预览

文档简介
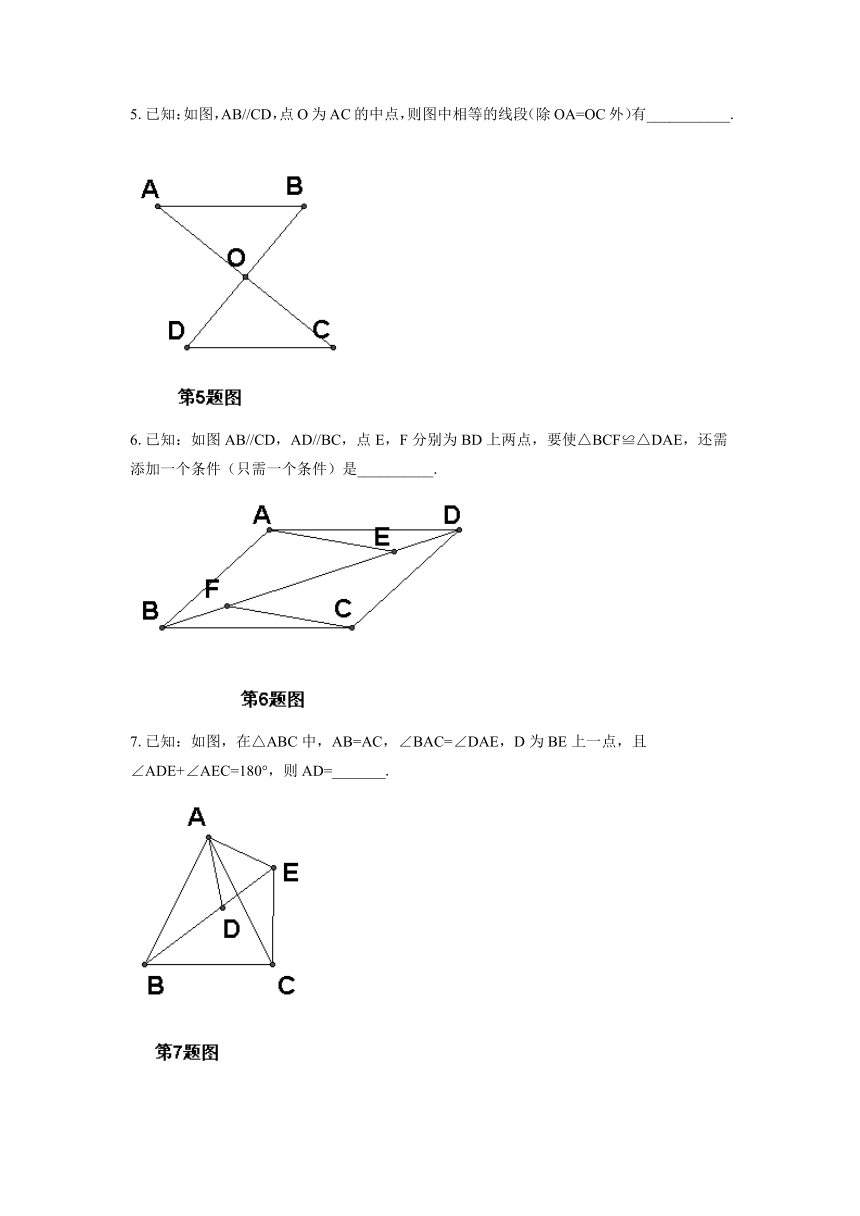
2020春北师大版七下数学4.2图形的全等同步测试1
1.如图,BC平分∠ABD,AB=DB,P为BC上一点,要证∠CAP=∠CDP,应先证_______≌_______;得__________=____________,___________=___________;继而有△PAC≌__________,理由是___________.
2.如图,△ABD≌△ACE,AE=3cm,AC=5cm,则CD=___________cm.
3.若两个图形全等,则其中一个图形可通过平移、__________或__________与另一个三角形完全重合.
4.如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是_________.
5.已知:如图,AB//CD,点O为AC的中点,则图中相等的线段(除OA=OC外)有___________.
6.已知:如图AB//CD,AD//BC,点E,F分别为BD上两点,要使△BCF≌△DAE,还需添加一个条件(只需一个条件)是__________.
7.已知:如图,在△ABC中,AB=AC,∠BAC=∠DAE,D为BE上一点,且∠ADE+∠AEC=180°,则AD=_______.
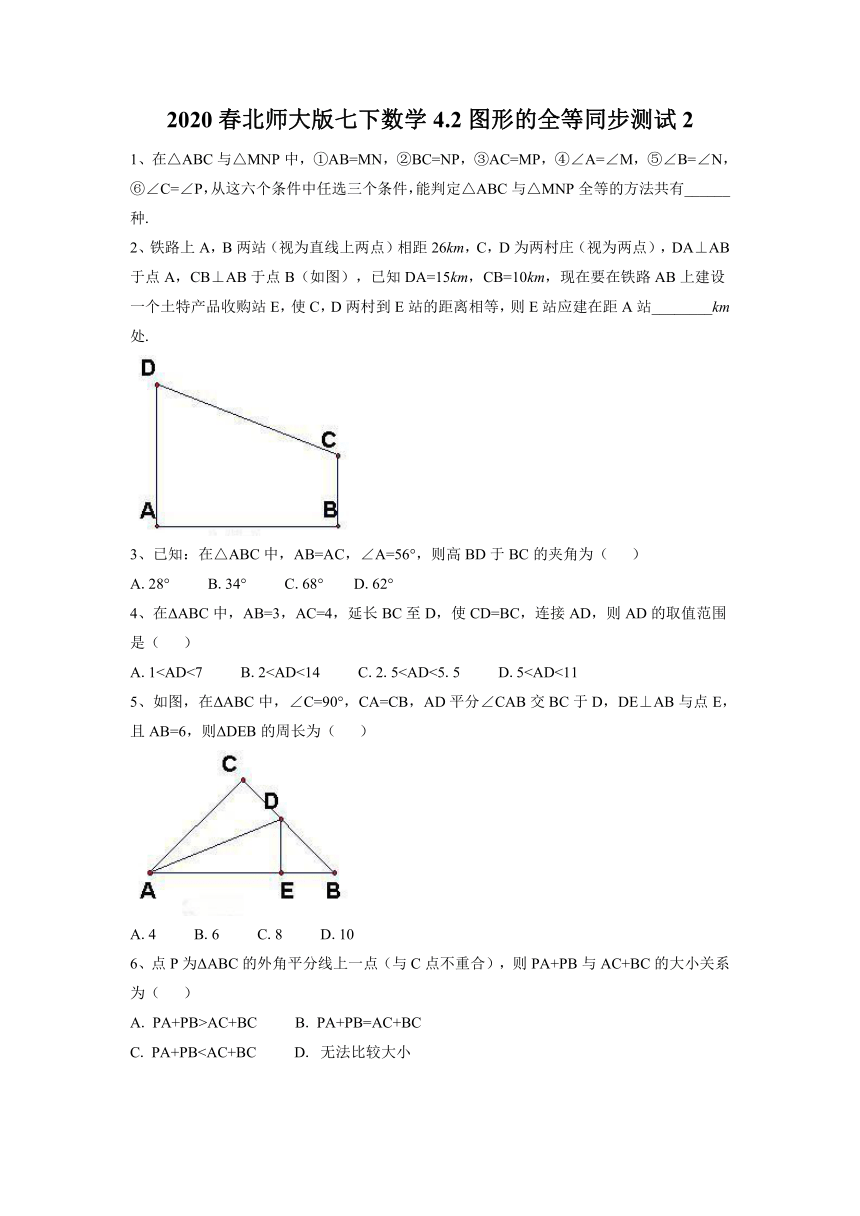
2020春北师大版七下数学4.2图形的全等同步测试2
1、在△ABC与△MNP中,①AB=MN,②BC=NP,③AC=MP,④∠A=∠M,⑤∠B=∠N,⑥∠C=∠P,从这六个条件中任选三个条件,能判定△ABC与△MNP全等的方法共有______种.
2、铁路上A,B两站(视为直线上两点)相距26km,C,D为两村庄(视为两点),DA⊥AB于点A,CB⊥AB于点B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站________km处.
3、已知:在△ABC中,AB=AC,∠A=56°,则高BD于BC的夹角为( )
A.28° B.34° C.68° D.62°
4、在ΔABC中,AB=3,AC=4,延长BC至D,使CD=BC,连接AD,则AD的取值范围是( )
A.15、如图,在ΔABC中,∠C=90°,CA=CB,AD平分∠CAB交BC于D,DE⊥AB与点E,且AB=6,则ΔDEB的周长为( )
A.4 B.6 C.8 D.10
6、点P为ΔABC的外角平分线上一点(与C点不重合),则PA+PB与AC+BC的大小关系为( )
A. PA+PB>AC+BC B. PA+PB=AC+BC
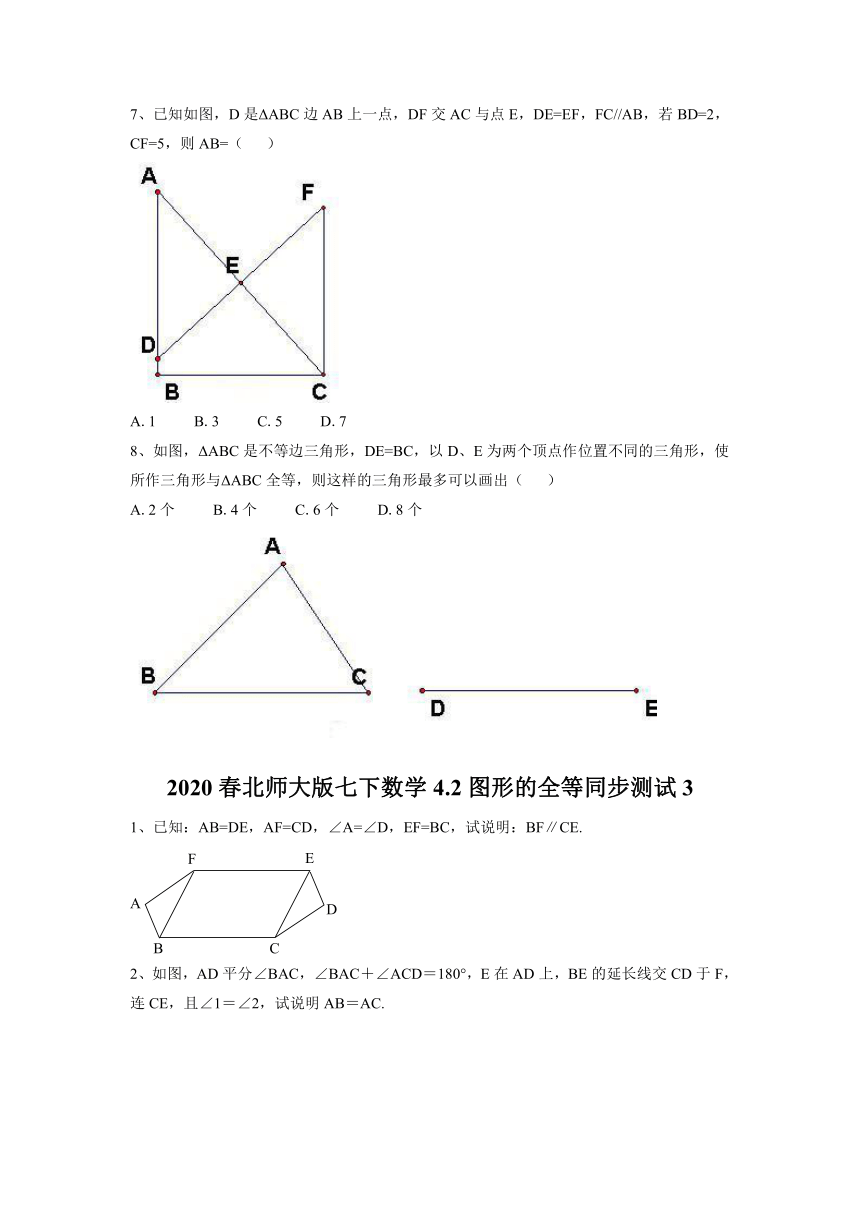
C. PA+PB7、已知如图,D是ΔABC边AB上一点,DF交AC与点E,DE=EF,FC//AB,若BD=2,CF=5,则AB=( )
A.1 B.3 C.5 D.7
8、如图,ΔABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与ΔABC全等,则这样的三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
2020春北师大版七下数学4.2图形的全等同步测试3
1、已知:AB=DE,AF=CD,∠A=∠D,EF=BC,试说明:BF∥CE.
2、如图,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC.
3、正方形网格中,小格的顶点叫做格点.小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形.小华在左边的正方形网格中作出了Rt⊿ABC.请你按照同样的要求,在右边的三个正方形网格中各画出一个直角三角形,并使四个网格中的直角三角形互不全等.
4、已知:正方形ABCD和正方形AEFG有一个公共点A, 点G、E分别在线段AD、AB上.
(1)如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
5、如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F,
(1)试说明F是AD中点;(2)求∠AEF的度数.
6、如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90o.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90o,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
2020春北师大版七下数学4.2图形的全等同步测试4
1.如图,在ΔABC中,AB=AC,高BD,CE交与点O,AO交BC于点F,则图中共有全等三角形( )
A.7对 B.6对 C.5对 D.4对
2.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB与点E,若ΔDEB的周长为10cm,则斜边AB的长为( )
A.8cm B.10cm C.12cm D.20cm
3.如图,ΔABC与ΔBDE均为等边三角形,ABA.AE=CD B.AE>CD C.AE4.已知∠P=80°,过不在∠P上一点Q作QM,QN分别垂直与∠P的两边,垂足为M,N则∠Q的度数等于( )
A.10° B.80° C.100° D.80°或100°
5.已知如图,在ΔABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为F,在直线CD上截取CD=AE.
求证:
(1)BD⊥BC;
(2)若AC=12cm,求BD的长.
6.探究题:“有两边及第三边上的高对应相等的两个三角形全等”这一命题是否成立?若成立,请证之;若不成立,请试举一反例,并将命题作适当改正,使之成为一真命题.
1.如图,BC平分∠ABD,AB=DB,P为BC上一点,要证∠CAP=∠CDP,应先证_______≌_______;得__________=____________,___________=___________;继而有△PAC≌__________,理由是___________.
2.如图,△ABD≌△ACE,AE=3cm,AC=5cm,则CD=___________cm.
3.若两个图形全等,则其中一个图形可通过平移、__________或__________与另一个三角形完全重合.
4.如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是_________.
5.已知:如图,AB//CD,点O为AC的中点,则图中相等的线段(除OA=OC外)有___________.
6.已知:如图AB//CD,AD//BC,点E,F分别为BD上两点,要使△BCF≌△DAE,还需添加一个条件(只需一个条件)是__________.
7.已知:如图,在△ABC中,AB=AC,∠BAC=∠DAE,D为BE上一点,且∠ADE+∠AEC=180°,则AD=_______.
2020春北师大版七下数学4.2图形的全等同步测试2
1、在△ABC与△MNP中,①AB=MN,②BC=NP,③AC=MP,④∠A=∠M,⑤∠B=∠N,⑥∠C=∠P,从这六个条件中任选三个条件,能判定△ABC与△MNP全等的方法共有______种.
2、铁路上A,B两站(视为直线上两点)相距26km,C,D为两村庄(视为两点),DA⊥AB于点A,CB⊥AB于点B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站________km处.
3、已知:在△ABC中,AB=AC,∠A=56°,则高BD于BC的夹角为( )
A.28° B.34° C.68° D.62°
4、在ΔABC中,AB=3,AC=4,延长BC至D,使CD=BC,连接AD,则AD的取值范围是( )
A.1
A.4 B.6 C.8 D.10
6、点P为ΔABC的外角平分线上一点(与C点不重合),则PA+PB与AC+BC的大小关系为( )
A. PA+PB>AC+BC B. PA+PB=AC+BC
C. PA+PB
A.1 B.3 C.5 D.7
8、如图,ΔABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与ΔABC全等,则这样的三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
2020春北师大版七下数学4.2图形的全等同步测试3
1、已知:AB=DE,AF=CD,∠A=∠D,EF=BC,试说明:BF∥CE.
2、如图,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC.
3、正方形网格中,小格的顶点叫做格点.小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形.小华在左边的正方形网格中作出了Rt⊿ABC.请你按照同样的要求,在右边的三个正方形网格中各画出一个直角三角形,并使四个网格中的直角三角形互不全等.
4、已知:正方形ABCD和正方形AEFG有一个公共点A, 点G、E分别在线段AD、AB上.
(1)如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
5、如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F,
(1)试说明F是AD中点;(2)求∠AEF的度数.
6、如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90o.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90o,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
2020春北师大版七下数学4.2图形的全等同步测试4
1.如图,在ΔABC中,AB=AC,高BD,CE交与点O,AO交BC于点F,则图中共有全等三角形( )
A.7对 B.6对 C.5对 D.4对
2.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB与点E,若ΔDEB的周长为10cm,则斜边AB的长为( )
A.8cm B.10cm C.12cm D.20cm
3.如图,ΔABC与ΔBDE均为等边三角形,AB
A.10° B.80° C.100° D.80°或100°
5.已知如图,在ΔABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为F,在直线CD上截取CD=AE.
求证:
(1)BD⊥BC;
(2)若AC=12cm,求BD的长.
6.探究题:“有两边及第三边上的高对应相等的两个三角形全等”这一命题是否成立?若成立,请证之;若不成立,请试举一反例,并将命题作适当改正,使之成为一真命题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
